RBSE Class 10 Maths Important Questions Chapter 12 Areas Related to Circles

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 12 Areas Related to Circles Important Questions and Answers.

RBSE Class 10 Maths Chapter 12 Important Questions Areas Related to Circles

Objective Type Questions

Question 1.
The number π is
(A) rational
(B) irrational
(C) imaginary
(D) None of these
Answer:
(B) irrational

Question 2.
The radius of a circle is 7 cm, then its area is
(A) 154 cm²
(B) 308 cm²
(C) 44 cm²
(D) 606 cm²
Answer:
(A) 154 cm²

Question 3.
In the figure, O is the centre of the circle. The radius of the circle is 18 cm and ∠AOB = 30°, then the length of the smaller arc is

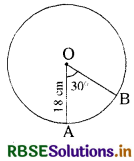
(A) 2π
(B) 3π
(C) 6π
(D) 4π
Answer:
(B) 3π

Question 4.
The circumference of a circle is 176 cm, then its radius is
(A) 21 cm
(B) 14 cm
(C) 28 cm
(D) 7 cm
Answer:
(C) 28 cm

Question 5.
The radius of a segment is 5 cm. The area of the sector of this circle formed by an arc of length 9 cm is
(A) 45 cm²
(B) 22.5 cm²
(C) 67.5 cm²
(D) 2.25 cm²
Answer:
(B) 22.5 cm²

Question 6.
The external and internal diameters of a circular path are 10 m and 6 m respectively. The area of the circular path is
(A) 25π m²
(B) 16π m²
(C) 9π m²
(D) 7π m²
Answer:
(B) 16π m²

Very Short Answer Type Questions

Question 1.
The circumference of a circle is 14π cm. Write its radius.
Solution:
Circumference = 2πr
2πr = 14π
∴ r = 7 cm

Question 2.
What is called the circumference of the circle?
Solution:
The distance covered by travelling once around a circle is called the circumference of the circle.

Question 3.
Which Indian Mathematician calculated the value of π?
Solution:
Indian Mathematician Aryabhatta calculated the value of π.

Question 4.
Write the formula for the area bounded by two concentric circles.
Solution:
\(\pi\left(r_{1}^{2}-r_{2}^{2}\right)\)

Question 5.
The radii of the two circles are respectively 6 cm and 4 cm. Write the ratio of their areas.
Solution:
Area of first circle = πr²
= π(6)²
= 36π cm²
Area of second circle = πr²
= π × (4)²
= 16π cm²
Taking ratio = \(\frac{36 \pi}{16 \pi}=\frac{9}{4}\) = 9 : 4

Question 6.
Find the value of the angle subtended by the minute hand of a clock in the centre in 20 minutes.
Solution:
Subtended angle = \(\frac{360^{\circ}}{60} \times 20\) = 120°

Question 7.
Find the area of the sector the length of whose arc is 10 cm and radius is 6 cm.
Solution:
Here radius (r) = 6 cm
arc (L) = 10 cm
Area of sector = \(\frac{1}{2}\) × L × r
= \(\frac{1}{2}\) × 10 × 6
= 30 cm²

Question 8.
The angle of a sector cut from a circle of radius 21 cm is 60°. Find the length of the arc and area of the sector.
Solution:
Radius r = 21 cm
Angle of sector θ = 60°
Length of the arc subtending angle θ at the centre

Question 9.
Find the circumference of a circle whose diameter is 14 cm.
Solution:
Diameter = 14 cm.
∴ Radius (r) = \(\frac{14}{2}\) = 7 cm
∴ Circumference = 2πr
= \(2 \times \frac{22}{7} \times 7\)
= 44 cm

Question 10.
The ratio of the circumferences of two circles is 2 : 3. Find the ratio of their radii.
Solution:
Let the radii of the two circles be r₁ and r₂ respectively.
⇒ \(\frac{2 \pi r_{1}}{2 \pi r_{2}}=\frac{2}{3}\)
⇒ \(\frac{r_{1}}{r_{2}}=\frac{2}{3}\)
⇒ r₁ : r₂ = 2 : 3

Question 11.
If the perimeter and area of a circle are numerically equal then find the radius of the circle.
Solution:
Let the radius of the circle = r
∴ According to the question,
Perimeter of circle = Area of the circle
⇒ 2πr = πr²
⇒ r = 2 units

Question 12.
Write the area of that sector of a circle of radius R whose angle is θ°.
OR
Write the area of a sector of a circle of radius r, whose angle in degrees is θ.
Solution:
Area of sector = \(\frac{\theta}{360^{\circ}} \times \pi R^{2}\) square units
OR
Area of sector = \(\frac{\theta}{360^{\circ}} \times \pi r^{2}\) square units

Question 13.
Write the length of the corresponding arc of a sector of a circle of radius r, whose angle in degrees is θ.
OR
Write the formula for the length of the corresponding arc of a sector of a circle of radius r, whose angle in degree is θ.
Solution:
Length of the corresponding arc of the sector of angle θ = \(\frac{\theta}{360^{\circ}} \times 2 \pi r\)

Question 14.
If the radius of a circle is 14 cm, then find the area of the circle.
Solution:
Here, Radius of circle (r) = 14 cm
∴ Area of circle = πr²
= \(\frac{22}{7}\) × (14)²
= \(\frac{22}{7}\) × 14 × 14
= 22 × 2 × 14
= 616 cm²

Question 15.
Find the area of circle with circumference 44 cm.
Solution:
According to the question,
Circumference = 44 cm
2πr = 44
∴ r = \(\frac{44 \times 7}{2 \times 22}\) = 7 cm
∴ Area of circle = πr²
= \(\frac{22}{7}\) × 7 × 7
= 154 cm²

Short Answer Type Questions

Question 1.
The cost of fencing a circular field at the rate of ₹ 24 per metre is ₹ 5280. The field is to be ploughed at the rate of ₹ 0.50 per m². Find the cost of ploughing the field (Take π = \(\frac{22}{7}\)).
Solution:
Length of the fence (in metres) = \(\frac{Total Cost}{Rate}\)
= \(\frac{5280}{24}\)
= 220
So the circumference of the field = 220 m
Therefore, if r metres is the radius of the field, then
2πr = 220
2 × \(\frac{22}{7}\) × r = 220
r = \(\frac{220 \times 7}{2 \times 22}\) = 35
i.e., the radius of the field is 35 m.
Therefore, area of the field = πr²
= \(\frac{22}{7}\) × 35 × 35 m²
= 22 × 5 × 35 m²
Now, cost of ploughing 1 m² of the field = ₹ 0.50
So, total cost of ploughing the field = 22 × 5 × 35 × 0.50 = ₹ 1925

Question 2.
In the figure, the radius of the semicircle is 7 cm. Find the area of the circle formed in the semicircle.
Solution:
In the given figure,
radius of the semicircle is equal to the diameter of the circle formed inside the semicircle.

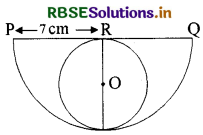
i.e., radius of the circle formed inside (r) = \(\frac{\mathrm{PQ}}{2}\)
⇒ r = \(\frac{7}{2}\) cm = 3.5 cm
∴ Area of the circle formed inside = πr²
= \(\frac{22}{7}\) × 3.5 × 3.5 cm²
= 38.5 cm²

Question 3.
Find the area of a quadrant of a circle whose circumference is 22 cm.
Solution:
Circumference of circle = 22 cm
⇒ 2πr = 22
⇒ r = \(\frac{22}{2 \pi}=\frac{22}{2 \times \frac{22}{7}}\)
⇒ r = \(\frac{7}{2}\) cm
Central angle (quadrant) (θ) = 90°
∴ Area of quadrant = \(\frac{\pi r^{2} \theta}{360^{\circ}}\)
= \(\frac{\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{77}{8}\) cm²
Area of quadrant = 9.625 cm²

Question 4.
An arc of a circle of radius 21 cm. subtends an angle of 60° at the centre, then find the area of the corresponding major sector.
Solution:
Given the Radius of the circle r = 21 cm
Area of the major sector formed by the arc

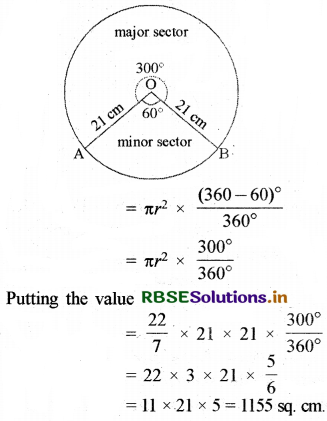
Question 5.
Find the area of the shaded region in Fig., where ABCD is a square of side 14 cm.
Solution:
Area of square ABCD = 14 × 14 cm² = 196 cm²
Diameter of each circle = \(\frac{14}{2}\) = 7 cm
So, Radius of each circle = \(\frac{7}{2}\) cm
So, Area of one circle = πr²
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) cm²
= \(\frac{154}{4}\) cm²
= \(\frac{77}{2}\) cm²
Therefore, area of the four circles = 4 × \(\frac{77}{2}\) cm² = 154 cm²
Hence, area of the shaded region = (196 - 154) cm² = 42 cm²

Question 6.
Find the area of the shaded design in Fig., where ABCD is a square of a side 10 cm and semicircles are drawn with each side of the square as diameter. (Use π = 3.14)

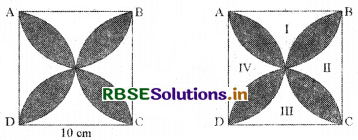
Solution:
Let us mark the four unshaded regions as I, II, III, and IV (see Fig.)
Area of I + III = Area of ABCD - Areas, of two semicircles of each radius of 5 cm.
= \(\left(10 \times 10-2 \times \frac{1}{2} \times \pi \times 5^{2}\right)\) cm²
= (100 - 3.14 × 25) cm²
= (100 - 78.5) cm²
= 21.5 cm²
Similarly, Area of II + Area of IV = 21.5 cm²
So, area of the shaded design = Area of ABCD - Area of (I + II + III + IV)
= (100 - 2 × 21.5) cm²
= (100 - 43) cm²
= 57 cm²

Question 7.
Find the area of a corresponding major sector of a circle with a radius of 7 cm and an angle of 120°.
Solution:
Given that,
Radius (R) = 7 cm
Angle at centre = 120°

= \(\frac{308}{3}\) cm²

Long Answer Type Questions

Question 1.
In the figure, PQRS is a rectangle. Side PQ = 10 cm and QR = 7 cm. Circles of radii 3 cm are drawn from each vertex of the rectangle. Find the area of the shaded region.
Solution:

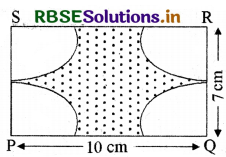
Area of rectangle PQRS = PQ × QR
= 10 × 7
= 70 cm²
Each angle of a rectangle is 90°.
Therefore areas of all the four sectors will be the same.

Area of the shaded region = (Area of the rectangle - Area of four sectors)
= (70 - 38.5) cm²
= (31.5) cm²
Hence the area of the shaded region = 31.5 cm²

Question 2.
Find the area of the shaded region in the figure.

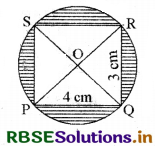
Solution:
In the given figure
PR = \(\sqrt{(P Q)^{2}+(Q R)^{2}}\)
⇒ PR = \(\sqrt{16+9}\) cm
⇒ PR = \(\sqrt{25}\) cm
⇒ PR = 5 cm
Radius of circle (OP) = \(\frac{\mathrm{PR}}{2}\)
= \(\frac{5}{2}\) cm
= 2.5 cm
∴ Area of circle = πr²
= \(\frac{22}{7}\) × 2.5 × 2.5 cm²
= 19.642 cm²
Area of rectangle PQRS = PQ × QR
= 4 × 3 cm²
= 12 cm²
∴ Area of the shaded region = (Area of circle - Area of rectangle)
= (19.642 - 12) cm²
= 7.642 cm²

Question 3.
In the figure, O is the centre of the semicircle, and the radius of the semicircle is 5 cm. If PR = 8 cm, then find the area of the shaded region.
Solution:
Area of semicircle = \(\frac{\pi r^{2}}{2}\)
= \(\frac{22}{7} \times \frac{5 \times 5}{2}\) cm²
= \(\frac{275}{7}\) cm²
= 39.28 cm²

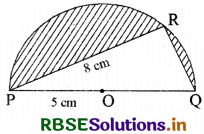
In ∆PQR, PQ = 2PO
⇒ PQ = 2(5) cm
⇒ PQ = 10 cm
QR = \(\sqrt{(P Q)^{2}-(P R)^{2}}\) (By Pythagoras Theorem) 
⇒ QR = \(\sqrt{(10)^{2}-(8)^{2}}\) cm
⇒ QR = \(\sqrt{100-64}\) cm
⇒ QR = \(\sqrt{36}\) = 6 cm
Area of ∆PQR = \(\frac{1}{2}\) × QR × PR
= \(\frac{1}{2}\) × 6 × 8 cm²
= 3 × 8 cm²
= 24 cm²
Area of shaded region = (Area of semicircle - Area of triangle PQR)
= (39.28 - 24) cm²
= 15.28 cm²
∴ Area of the shaded region = 15.28 cm²

Question 4.
In the figure, PQRS is a square where one side is 7 cm. At each vertex of the square circles of radius 3.5 cm have been drawn. Find the area of the shaded region.

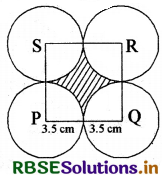
Solution:
In the adjacent figure side of the square = 7 cm
Area of square = 7 × 7 cm² = 49 cm²
In the given figure all the four circles are of the same area.
From these circles, sectors are cut.
Angle of sector in four circles (θ) = 90°
Radius (r) = 3.5 cm
The areas of all the four sectors will be the same.
So, area of four sectors = \(4 \times \frac{\pi r^{2} \theta}{360^{\circ}}\)
= \(4 \times \frac{22}{7} \times \frac{3.5 \times 3.5 \times 90^{\circ}}{360^{\circ}}\) cm²
= \(\frac{22}{7}\) × 3.5 × 3.5 cm²
= 38.5 cm²
Area of the shaded region = (Area of square - Area of four sectors)
= (49 - 38.5) cm²
= 10.5 cm²

Question 5.
In fig., two circular flower beds have been shown on two .sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn And the sum of the areas of the lawn and the flower beds.
Solution:
Area of the square lawn ABCD = Side × Side = 56 × 56 cm² ......(1)

Question 6.
Two circles touch externally. If the sum of their areas is 130π cm² and the distance between their centres is 14 cm, then find the radii of these circles.
Solution:
Let c₁ and c₂ be the centres of the given circles and their radii are r₁ and r₂ respectively.

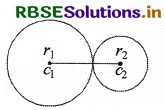
Since both the circles touch externally
c₁c₂ = r₁ + r₂
⇒ 14 = r₁ + r₂
⇒ r₁ + r₂ = 14 .....(i)
According to the question,
sum of the areas of the two circles = 130π cm²

Adding equations (i) and (iv)
2r₁ = 22
∴ r₁ = 11 cm
Putting the value of r₁ in equation (i) we get r₂ = 3 cm
Hence the radii of the two circles are 11 cm and 3 cm respectively.

Question 7.
In the adjacent figure there is a right-angled triangle at vertex point A of ΔABC where AB = 6 cm, BC = 10 cm and I is the incentre of triangle ABC, then find the area of the shaded region.
Solution:

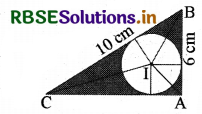
In right ΔABC
⇒ (BC)² = (AB)² + (AC)²
⇒ (AC)² = (BC)² - (AB)²
⇒ (AC)² = (10)² - (6)²
⇒ (AC)² = 100 - 36
⇒ (AC)² = 64
⇒ AC = 8 cm
∴ Area of ΔABC = \(\frac{1}{2}\) × AB × AC
⇒ Area of ΔABC = \(\frac{1}{2}\) × 6 × 8 = 24 cm²
Let the radius of the incircle be r cm
∴ Area of ΔABC - Area of ΔIBC + Area ΔICA + Area of ΔIAB
⇒ 24 = \(\frac{1}{2}\) (BC × r) + \(\frac{1}{2}\) (AC × r) + \(\frac{1}{2}\) (AB × r)
⇒ 24 = \(\frac{1}{2}\) r (BC + AC + AB)
⇒ 24 = \(\frac{1}{2}\) × r × (10 + 8 + 6)
⇒ 24 = \(\frac{1}{2}\) × r × 24
⇒ 24 = 12r
⇒ r = 2
∴ Area of the shaded region = Area of ΔABC - Area of incircle
= 24 - πr²
= 24 - \(\frac{22}{7} \times(2)^{2}\)
= 24 - \(\frac{22}{7} \times 4\)
= \(\frac{80}{7}\) cm²

Question 8.
Find the area of the sector of a circle with a radius of 4 cm and of angle 60°. Also, find the area of the corresponding major sector. (Use π = 3.14)

Solution:
According to the question,
Radius of the sector of a circle (R) = 4 cm
Central angle (θ) = 60°

So the area of the sector = 8.37 cm²
Area of the corresponding major sector

= \(\frac{15}{18}\) × 3.14 × 16
= 41.87 cm²

Question 9.
In the figure find the area of the shaded region, if AB = 5 cm, AC = 12 cm, and O is the centre of the circle.

Solution:
The figure given inside the circle is A = right angled triangle whose base 12 cm and perpendicular = 5 cm.
So in ∆ABC
CB² = CA² + AB²
= (12)² + (5)²
= 144 + 25
= 169
∴ CB² = 169
∴ Hypotenuse CB = \(\sqrt{169}\) = 13 cm
Area of right triangle = \(\frac{1}{2}\) × 12 × 5
= 6 × 5
= 30 cm²
∴ Required shaded area = Area of semicircle - Area of ∆ABC

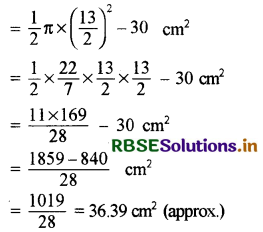
i.e., area of the shaded region = 36.39 cm²