RBSE Class 10 Maths Important Questions Chapter 11 Constructions

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 11 Constructions Important Questions and Answers.

RBSE Class 10 Maths Chapter 11 Important Questions Constructions

Objective Type Questions

Question 1.
In which case the construction of the triangle cannot be done.
(A) If the three angles are given
(B) If the three sides are given
(C) If two angles and one side are given
(D) If two sides and the angle between them is given
Answer:
(A) If the three angles are given

Question 2.
To divide a line segment in a given ratio we make at the point of the line segment.
(A) reflex angle
(B) obtuse angle
(C) right angle
(D) acute angle
Answer:
(D) acute angle

Question 3.
The line segment, which passes through the centre of a circle and where both the ends lie on the circle, is called
(A) radius
(B) diameter
(C) sector
(D) segment
Answer:
(B) diameter

Question 4.
A straight line that touches the circumference of the circle at only one point is called
(A) secant
(B) tangent
(C) isosceles line
(D) divided line
Answer:
(B) tangent

Question 5.
The number of tangent lines drawn from an external point to a circle can be
(A) 2
(B) 3
(C) 0
(D) 4
Answer:
(A) 2

Question 6.
In the given figure the tangent line is

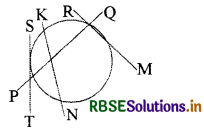
(A) PQ
(B) ST
(C) PM
(D) KN
Answer:
(B) ST

Question 7.
In the given figure the number of tangent lines is

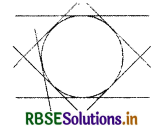
(A) 4
(B) 5
(C) 6
(D) 7
Answer:
(D) 7

Very Short Answer Type Questions

Question 1.
Two circles touch each other internally, then write the number of their common tangent lines.
Answer:
One

Question 2.
How many chords of a circle can be drawn?
Answer:
Infinitely many chords
 
Question 3.
From any point situated outside a circle how many tangent lines can be drawn.
Answer:
Two

Question 4.
PQ is a secant of a circle, write the condition for secant PQ to become a tangent line.
Answer:
When points P and Q are coincident i.e. both the points are the same then secant PQ will be called a tangent line.

Question 5.
What is the relation between the tangent line and the radius of a circle?
Answer:
The radius drawn through the point of contact of the circle and the tangent line is perpendicular to each other.

Question 6.
The length of a tangent line drawn to a circle from any external point is 12 cm, if the radius of the circle is 5 cm, then find the distance of the external point from the centre.
Answer:
Distance = \(\sqrt{(12)^{2}+(5)^{2}}\)
= \(\sqrt{144+25}\)
= \(\sqrt{169}\)
= 13 cm

Question 7.
Write the name of the secant in the given figure.

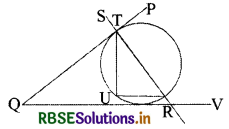
Answer:
Secant = SR

Question 8.
In the given figure write the number of the tangent lines.

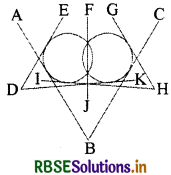
Solution:
Tangent lines - ED, DK, AB, BC, HG and HI.
Hence total number = 6

Question 9.
Construct a tangent line at any point of a circle of radius 3 cm.
Solution:

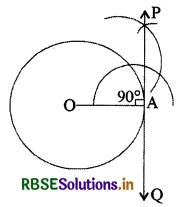
Short Answer Type and Long Answer Type Questions

Question 1.
Construct a triangle ABC where sides are 7.5 cm, 7 cm, and 6.5 cm. Construct a triangle similar to ∆ABC where each side is \(\frac{2}{3}\)rd part of the corresponding side of ∆ABC.
Solution:
Steps of Construction:
(i) Draw a line BC = 7.5 cm.
(ii) From B draw arc BA = 6.5 cm and from C draw arc CA = 7.0 cm which meets at point A. Joining these we get DABC.
(iii) At point B of BC draw a line BX below BC making an acute angle.

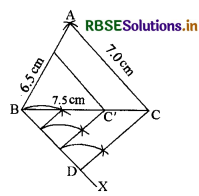
(iv) Divide BX into 3 equal parts of 1 cm starting from B. The end of the third part is D. Join D to C.
(v) With the help of the compass draw lines from each point of BD making angles equal to ∠BDC which meet at BC. Thus we get these equal parts of BC also.
(vi) Out of the three equal parts of MC, mark C' at the end of the second part.
(vii) Through C' draw a line parallel to CA which meets BA at A'.
Thus we get ∆A'BC' similar to ∆ABC.

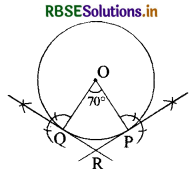
Question 2.
Draw a circle of radius 3.2 cm. At its two points draw two radii making an angle of 70°. Draw the tangent lines to the circle at these points where their radii meet the circle.
Solution:
Steps of Construction:
(i) Draw a circle of radius 3.2 cm and make an angle POQ of 70° at its centre.
(ii) On constructive right angles at points Q and P we shall get the tangent line RQ and RP.

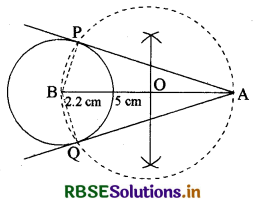
Question 3.
Draw a line segment of length AB = 5 cm. Taking B as centre draw a circle of radius 2.2 cm and draw tangent lines to this circle from point A.
Solution:
Steps of Construction:
(i) Draw a line AB = 5 cm. Taking point B as centre draw a circle of radius 2.2 cm.
(ii) Find the mid-point O of AB and taking O as centre draw a circle of radius OA.
This circle cuts the former circle at points P and Q. Joining P and Q with A we get the tangent lines PA and AQ.

Question 4.
Construct a triangle PQR in which PQ = 6 cm, ∠Q = 70° and QR = 5.7 cm. Convert it into a similar triangle the ratio of whose sides and the corresponding sides of ∆PQR be \(\frac{3}{5}\). Write the main steps of the construction.
Solution:
Steps of Construction:
(i) Construct the given triangle PQR.
(ii) Draw a line QX at point Q of QR below QR making an acute angle with QR.
(iii) Divide QX into five equal parts each of 1 cm starting from Q. The end of the fifth point is D. Join D to R.

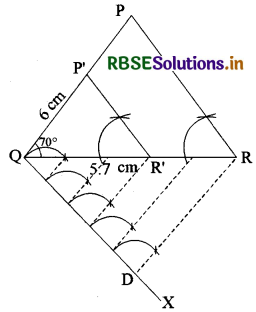
(iv) With the help of a compass from each equal part of QD draw lines making angles equal to ∠QDR which meet at QR. These are the five equal parts of QR also.
(v) Out of the five equal parts of QR mark R' at the end of the third part.
(vi) Through R' draw a line parallel to RP which meets QP at P'.
Thus, ∆P'QR' is a triangle similar to ∆PQR.

Question 5.
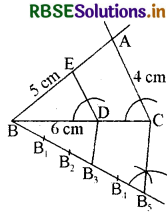
Construct a triangle similar to a given triangle ABC, whose sides are \(\frac{3}{4}\) of the corresponding sides of the given triangle (i.e. scale factor is \(\frac{3}{4}\))
Solution:
A triangle ABC is given. We are to construct another triangle, whose sides are \(\frac{3}{4}\) of the corresponding sides of triangle ABC.
Construction:
1. First of all draw a ray BX from the end B of BC on the side opposite the vertex A.
2. Now locate 4 points (the greater number of 3 and 4 in \(\frac{3}{4}\)) B₁, B₂, B₃ and B₄ on B_X such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄

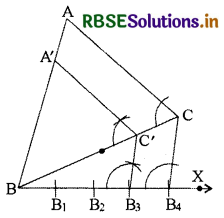
3. Join B₄C and draw a line through B₃ (the third point, 3 being smaller of 3 and 4 in \(\frac{3}{4}\)) parallel to B₄C intersecting BC at C'.
4. Through C' draw a line BA parallel to CA intersecting BA at A'.
Then, ∆A'BC' is the required triangle.
Justification:

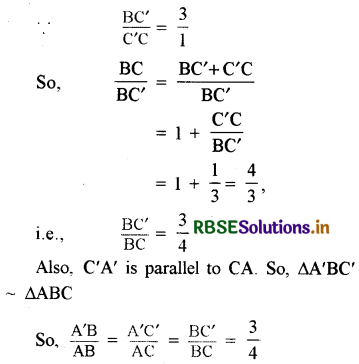
Question 6.
Construct a triangle similar to a given triangle ABC, whose sides are \(\frac{5}{3}\) of the corresponding sides of triangle ABC (i.e. scale factor in \(\frac{5}{3}\))
Solution:
A triangle ABC is given. We are to construct a triangle, whose sides are \(\frac{5}{3}\) of the corresponding sides of ∆ABC.
Construction:
1. First of all draw a ray BX making an acute angle with BC on the side opposite to the vertex A.
2. Locate 5 (the greater number of 5 and 3 in \(\frac{5}{3}\)) points B₁, B₂, B₃, B₄ and B₅ on B_X such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
3. Now Join B₃ (the third point 3 being smaller than 5 and 3 in \(\frac{5}{3}\)) to C and through B₅ draw a line parallel to B₃C which intersects the line segment BC produced at C'.
4. Through C' draw a line parallel to CA intersecting the line segment BA produced at A'.
Then, A'BC' is the required triangle.

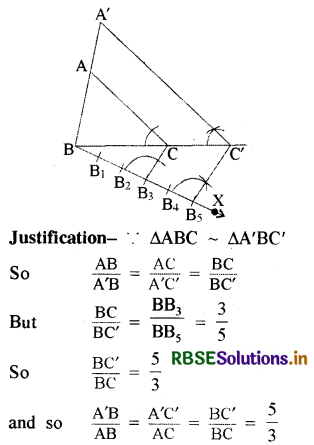
Question 7.
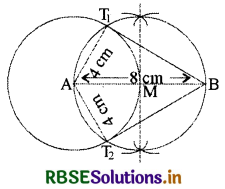
Draw a line segment of length 8 cm. Taking A as centre draw a circle of radius 4 cm and from the point, B draw a pair of tangent lines to this circle and measure their lengths.
Solution:
Given Line segment AB = 8 cm with A as centre a circle of radius 4 cm is drawn.
Construction:
1. Draw line segment AB = 8 cm.
2. With A as centre, draw a circle of radius 4 cm.
3. Now we bisect the line segment AB with the help of a compass Thus we get the mid-point M of AB.
4. Taking M as centre draw a circle of diameter AB which cuts the circle with centre A at points T₁ and T₂.
5. Draw line segments T₁B and T₂B. Therefore, T₁B and T₂B are the tangent lines to the circle with centre A and measuring these we get T₁B = T₂B = 6.9 cm

Question 8.
Divide a line segment of 7.5 cm into the ratio of 2 : 3. Draw figure only.
Solution:

Question 9.
On a circle of radius 3 cm, draw a tangent line from any point of a concentric circle of radius 5 cm and measure its length.
Solution:
Steps of Construction:
1. First of all from point O draw two concentric circles of radius 3 cm and 5 cm.

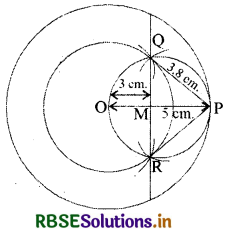
2. Mark any point P on the circumference of the larger circle.
3. Now join OP and bisect it and mark its mid-point as M.
4. Now taking M as centre draw a circle with radius MP which intersects the circle at Q and R.
5. Now join PQ and PR and thus PQ and PR will be the derived tangent lines.
Length of the tangent lines = RP = PQ = 3.8 cm.

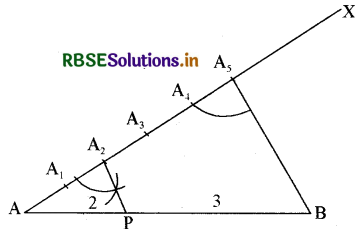
Question 10.
Construct a triangle of sides 4 cm, 5 cm, and 6 cm, and then a triangle similar to it whose sides are \(\frac{3}{5}\) times of the corresponding sides of the given triangle.
Solution:
Steps of Construction:
1. First of all draw a line segment BC = 6 cm.
2. Now taking B as centre and radius of 5 cm, draw an arc.
3. With C as the centre and a radius of 4 cm, draw an arc to intersect the former arc at A.

4. Join AB and AC. Then ∆ABC is the required triangle.
5. Make an acute angle below BC.
6. On B_X, mark five points B₁, B₂, B₃, B₄, and B₅ such that BB₁ = B₁B₂ = B₂B₃
7. Now join B₅C.
8. Through B₂ draw B₃D || B₅C which meets BC at D.
9. Through D draw ED || AC which meets BA at E.
Thus ∆EBD is the required triangle whose sides are \(\frac{3}{5}\) times the corresponding sides of ∆ABC.
Justification:
Since DE || CA
∆ABC ~ ∆EBD
and \(\frac{\mathrm{EB}}{\mathrm{AB}}=\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{\mathrm{DE}}{\mathrm{CA}}=\frac{3}{5}\)
Thus, we get a new triangle that is similar to the given triangle, whose sides are \(\frac{3}{5}\) times the corresponding sides of the first triangle.