RBSE Class 10 Maths Important Questions Chapter 10 वृत्त

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 10 वृत्त Important Questions and Answers.

RBSE Class 10 Maths Chapter 10 Important Questions वृत्त

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
एक 6 सेमी. त्रिज्या वाले वृत्त पर किसी बाह्य | बिन्दु A से स्पर्श रेखा की लम्बाई 10 सेमी. है। बिन्दु A |से वृत्त के केन्द्र से दूरी होगी
(A) 7 सेमी.
(B) 8 सेमी.
(C) 9 सेमी.
(D) 10 सेमी.
उत्तर:
(B) 8 सेमी.

प्रश्न 2.
एक बिन्दु P वृत्त के केन्द्र से 25 सेमी. की दूरी पर है। वृत्त की त्रिज्या 7 सेमी. है और P से वृत्त की खींची गई स्पर्श रेखा की लम्बाई होगी
(A) \(\sqrt{30}\) सेमी.
(B) 24 सेमी.
(C) 28 सेमी.
(D) 30 सेमी.
उत्तर:
(B) 24 सेमी.

प्रश्न 3.
यदि एक समचतुर्भुज ABCD की चारों भुजाएँ एक वृत्त को स्पर्श करती हैं तो
(A) AC + DA = BD + CD
(B) AB + CD = BC + DA
(C) AB + CD = AC + BC
(D) AC + AD = BC + BD
उत्तर:
(B) AB + CD = BC + DA

प्रश्न 4.
वह रेखा जो वृत्त को दो बिन्दुओं पर काटती है, कहलाती है
(A) जीवा
(B) स्पर्श रेखा
(C) छेदक रेखा
(D) इनमें से कोई नहीं
उत्तर:
(C) छेदक रेखा

प्रश्न 5.
एक वृत्त के बाह्य बिन्दु से खींची गई अधिकतम स्पर्श रेखाएँ हैं
(A) एक
(B) दो
(C) तीन
(D) अनन्त
उत्तर:
(B) दो

प्रश्न 6.
किसी वृत्त के व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर होती हैं
(A) लम्बवत्
(B) समान्तर
(C) प्रतिच्छेदी
(D) इनमें से कोई नहीं
उत्तर:
(B) समान्तर

प्रश्न 7.
दी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएँ हैं, 0 वृत्त का केन्द्र है, यदि ∠CAB = 60° तो ∠BDC है

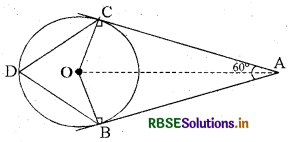
(A) 60°
(B) 70°
(C) 120°
(D) 150°
उत्तर:
(A) 60°

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
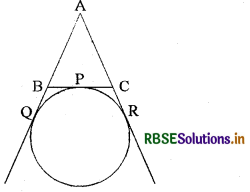
दी गई आकृति में ΔABC का बहिर्वृत्त, भुजाओं को Q, Pएवं R पर स्पर्श करता है। यदि AQ = 8 सेमी. हो तों ΔABC का परिमाप ज्ञात कीजिए।
हल:
हम जानते हैं कि
AQ = \(\frac{1}{2}\) परिमाप (ABC)
परिमाप ΔABC = 2 × AQ
= 2 × 8 = 16 सेमी.

प्रश्न 2.
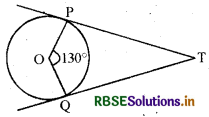
चित्र में यदि TP और TQ केन्द्र 0 वाले वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 150° तो ∠PTQ का मान ज्ञात कीजिये।

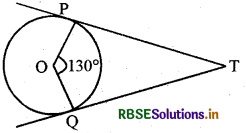
हल:
PT व QT स्पर्श रेखाएँ हैं।
∴ ∠POQ + ∠PTO = 180°
⇒ 130° + ∠PTQ= 180°
⇒ ∠PTQ = 180° - 130° = 50°

प्रश्न 3.
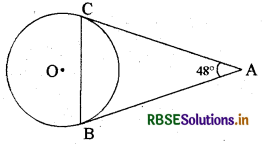
दिये गये चित्र में, बाह्य बिन्दु A से वृत्त की दो स्पर्श रेखाएँ AB व AC खींची गई हैं। यदि ∠BAC = 480 हो, तो ∠ABC का मान लिखिए।
हल:
∠B + ∠C = 180° - 48°
= 132°
लेकिन ∠B= ∠C
स्पर्श रेखाएँ लम्बाई में बराबर होती हैं।

∴ ∠ABC = \(\frac{132^{\circ}}{2}\)
= 66°

प्रश्न 4.
चित्र में AB, BC तथा CA वृत्त की स्पर्श रेखाएँ हैं। यदि BC = 6.3 सेमी. तथा MC = 2.7 1 सेमी. हो, तो BL की नाप लिखिए।
उत्तर:
हम जानते हैं
MC = NC स्पर्श रेखाओं की लम्बाई बराबर होती है।

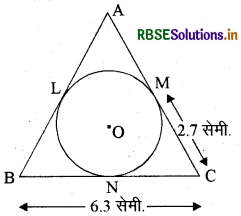
BN = (6.3 - 2.7)
BN = 3.6 सेमी.
और BN = BL है।
BL = 3.6 सेमी.

प्रश्न 5.
दो वृत्त बाह्यतः स्पर्श करते हैं। यदि दोनों वृत्तों की त्रिज्याएँ क्रमशः 5 सेमी. तथा 3 सेमी. हों, तो उनके केन्द्रों के बीच की दूरी लिखिए।
उत्तर:
5 + 3 = 8 सेमी.।

प्रश्न 6.
दो वृत्त एक-दूसरे को अन्तः स्पर्श करते हैं, तो उनकी उभयनिष्ठ स्पर्श रेखाओं की संख्या लिखिए।
उत्तर:
एक।

प्रश्न 7.
दिए गए चित्र में PA व PB वृत्त की स्पर्श रेखाएँ हैं। ∠APB = 30° है तो ∠AOB का मान लिखिए।

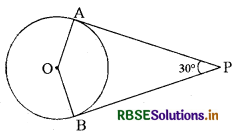
उत्तर:
∠AOB = 180° - 30° = 150°

प्रश्न 8.
दिए गए चित्र में PBQ, बिन्दु B पर वृत्त की स्पर्श रेखा है। ∠ABP का मान लिखिए।

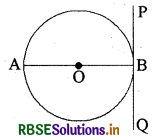
उत्तर:
∠ABP = 90°

प्रश्न 9.
किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखा की लम्बाई 12 सेमी. है, यदि वृत्त की त्रिज्या 5 सेमी है तो केन्द्र से बाह्य बिन्दु की दूरी बताइए।
उत्तर:
दूरी = \(\sqrt{(12)^{2}+(5)^{2}}=\sqrt{169}\) = 13 सेमी.

प्रश्न 10.
दिए गए चित्र में 0 वृत्त का केन्द्र है। AB |व AC वृत्त की स्पर्श रेखाएँ हैं। यदि OA = 10 सेमी. तथा OB = 6 सेमी. हैं तो AC की लम्बाई लिखिए।

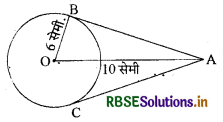
हल:
AB = \(\sqrt{10^{2}-6^{2}}\)
= \(\sqrt{100-36}\)
= \(\sqrt{64}\) = 8 सेमी.
तथा AB = AC अतः, AC = 8 सेमी.

प्रश्न 11.
चित्र में TP और TQ, O केन्द्र वाले वृत्त की स्पर्श रेखाएँ हैं। यदि ∠TOQ = 50° हो, तो ∠OTP ज्ञात कीजिये।

हल:
∵ QT एक स्पर्श रेखा है।
∴ ∠OQT = 90°
AOQT से ∠OTQ= 180° - (∠OQT + ∠QOT)
= 180° - (50° + 90)
= 180° - 140° = 40°

∵ ΔQOT ≅ ΔPOT (∵ PT = QT)
∠P = ∠Q = 90°
OT = OT
∴ ∠OTP = ∠OTQ
अतः ∠OTP = 40°

प्रश्न 12.
वृत्त की सतह पर स्थित बिन्दु पर कितनी | स्पर्श रेखाएँ खींची जा सकती हैं?
उत्तर:
वृत्त पर स्थित किसी बिन्दु से वृत्त पर एक और केवल एक ही स्पर्श रेखा खींची जा सकती है।

प्रश्न 13.
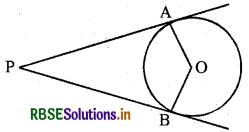
दिये गये चित्र में, यदि PA व PB, केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि कोण APB = 80°, तो कोण AOB का मान ज्ञात कीजिये।

हल:
चित्र में PA और PB, केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ हैं।
∴ ∠PAO = ∠PBO = 90°
और ∠APB = 80° दिया गया है।
∴ ∠AOB = 360° - (90° + 90° + 80°)
= 360° - 260° = 100°

प्रश्न 14.
यदि एक बिन्दु A से, O केन्द्र वाले किसी वृत्त पर AB व AC दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠BOC = 140° तो ∠BAC का मान लिखिये।
हल:
चित्र में AB और AC, केन्द्र 0 वाले किसी वृत्त पर दो स्पर्श रेखाएँ हैं।

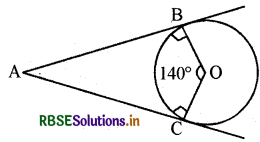
∴ ∠ABO = ∠ACO = 90° और ∠BOC = 140° दिया गया है।
∴ ∠BAC + ∠BOC = 180° होगा
अतः ∠BAC = 360° - (90° + 90° + 140°)
= 360° - 320° = 40°

प्रश्न 15.
5 सेमी. त्रिज्या वाले एक वृत्त के बिन्दु P, पर स्पर्श रेखा PQ केन्द्र 0 से जाने वाली एक रेखा के बिन्दु Q पर इस प्रकार मिलती है कि 00 = 13 सेमी. तो PQ की लम्बाई ज्ञात कीजिये।
हल:
प्रश्नानुसार आकृति बनाने पर

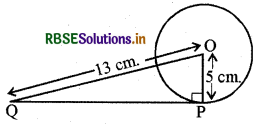
OP = 5 cm. और OQ = 13 cm.
∴ PQ एक स्पर्श रेखा है और OP त्रिज्या है।
∠OPQ = 90°

अब समकोण AOPQ में, पाइथागोरस प्रमेय से
(OQ)² = (OP)² + (PQ)²
मान रखने पर (13)² = (5)² + (PQ)²
169 = 25 + (PQ)²
या (PQ)² = 169 - 25 = 144
PQ= \(\sqrt{144}\) = 12 cm

प्रश्न 16.
यदि एक बिन्दु T से O केन्द्र वाले किसी वृत्त पर TA व TB स्पर्श रेखाएँ परस्पर 70° के कोण पर झुकी हों, तो ∠AOB को ज्ञात कीजिए।
हल:

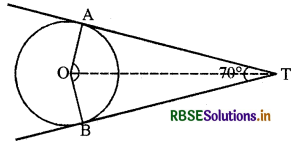
चित्रानुसार TA और TB, केन्द्र O वाले किसी बिन्दु . | पर दो स्पर्श रेखाएँ हैं।
∠TAO = ∠TBO = 90°
तथा ∠ATB = 70°
∠AOB = 360° – (90° + 90° + 70°)
= 360° - 250°
= 110°

प्रश्न 17.
यदि बिन्दु R से O केन्द्र वाले किसी वृत्त पर RA व RB स्पर्श रेखाएँ परस्पर ए के कोण पर झुकी हों तथा ∠AOB = 40° हो तो कोण e का मान ज्ञात करें।
हल:
RA व RB स्पर्श रेखाएँ हैं।
∴ ∠AOB + ∠ARB = 180°
⇒ 40° + ∠ARB = 180°
⇒ ∠ARB = 180° - 40°
= 140°

प्रश्न 18.
4 सेमी त्रिज्या वाले वृत्त पर स्थित किसी बिन्दु पर कितनी स्पर्श रेखाओं की रचना की जा सकती है?
उत्तर:
हम जानते हैं कि किसी भी वृत्त पर स्थित | बिन्दु पर एक और केवल एक ही स्पर्श रेखा खींची जा सकती है।

प्रश्न 19.
दी गयी आकृति में O एक वृत्त का केन्द्र है जिसके बाह्य बिन्दु से वृत्त पर दो स्पर्श रेखाएँ QP और QR खींची गई हैं। कोण POR का मान ज्ञात कीजिए।

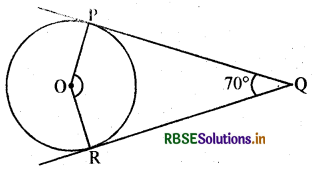
हल:
PQ व RQ स्पर्श रेखाएँ हैं।
∴ ∠POR + ∠PQR = 180°
∠POR + 70° = 180°
∠POR= 180° - 70°
= 110°

प्रश्न 20.
5 सेमी. त्रिज्या वाले वृत्त के केन्द्र से 9 सेमी. दूर बाह्य बिन्दु से वृत्त पर कितनी स्पर्श रेखाएँ खींची जा सकती है?
उत्तर:
हम जानते हैं कि वृत्त के बाहर स्थित किसी बिन्दु से जाने वाली वृत्त पर दो और केवल दो स्पर्श रेखाएँ होती हैं।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
सिद्ध कीजिए कि किसी बाह्य बिन्दु किसी वृत्त पर खींची गई दो स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।
अथवा
सिद्ध कीजिए कि एक बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।

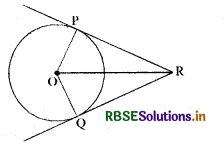
हल:
दिया है : वृत्त का केन्द्र O है और बाह्य बिन्दु R से दो स्पर्श रेखाएँ RP और RQ हैं।
सिद्ध करना है : RP = RQ
रचना : OP, OQ और OR को मिलाया।
उपपत्ति : हम जानते हैं कि स्पर्श रेखा, वृत्त की त्रिज्या पर लम्बवत् होती है।
अतः ∠OPR = ∠OQR = 90° .... (i)

अब ΔOPR और ΔOQR में,
∠OPR = ∠OQR = 90°

समीकरण (i) से
OR = OR (उभयनिष्ठ भुजा)
OP = OQ (वृत्त की त्रिज्याएँ)
∴ समकोण - कर्ण -- भुजा सर्वांगसमता गुणधर्म से.
ΔOPR ≅ ΔOQR
अतः सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होंगी।
⇒ RP = RQ (इतिसिद्धम्)

प्रश्न 2.
सिद्ध कीजिए कि दो संकेन्द्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिन्दु पर समद्विभाजित होती है।

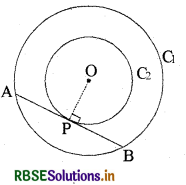
हल:
दिया है : हमें केन्द्र O वाले दो संकेन्द्रीय वृत्त C, और C, तथा बड़े वृत्त C, की जीवा AB, जो छोटे वृत्त C, को बिन्दु P पर स्पर्श करती है (देखिए आकृति)।
सिद्ध करना है : AP = BP रचना : आइए OP को मिलाएँ।
उपपत्ति : AB, C, के बिन्दु P पर स्पर्श रेखा है और OP त्रिज्या है।

अतः प्रमेय से, OP ⊥ AB
अब AB वृत्त C, की एक जीवा है और OP ⊥ AB है।
अतः, OP जीवा AB को समद्विभाजित करेगी क्योंकि केन्द्र से जीवा पर खींचा गया लम्ब उसे समद्विभाजित करता है,
अर्थात् AP = BP (इतिसिद्धम्)

प्रश्न 3.
यदि किसी वृत्त के किसी बाह्य बिन्दु से वृत्त पर दो स्पर्श रेखाएँ खींची जायें तो सिद्ध कीजिये कि
(i) वे रेखाएँ वृत्त के केन्द्र पर समान कोण बनाती हैं तथा
(ii) वृत्त के केन्द्र से मिलाने वाले रेखाखण्ड के साथ, दोनों स्पर्श रेखाएँ बराबर कोण बनाती हैं।
हल:
दिया है : एक वृत्त C(0, r) है जिसके बाह्य बिन्दु A से वृत्त पर दो स्पर्श रेखाएँ AP और AQ खींची गई हैं।
सिद्ध करना है- (i) ∠AOP = ∠AOQ
(ii) ∠OAP = ∠OAQ
रचना: OA, OP तथा OQ को मिलाया।

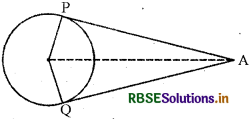
उपपत्ति-ΔOPA और ΔOQA में
AP = AQ(एक ही वृत्त की स्पर्श रेखाएँ)
OA = OA (उभयनिष्ठ भुजा)
OP = OQ (त्रिज्याएँ)

S-S-S सर्वांगसमता से
ΔΟΡΑ ≅ ΔOQA
⇒ ∠AOP= ∠AOQ (CPCT)
तथा ∠OAP = ∠OAQ (इतिसिद्धम्)

प्रश्न 4.
सिद्ध करो कि वृत्त की किसी जीवा के सिरों पर खींची गई स्पर्श रेखाएँ, जीवा से समान कोण बनाती हैं।
हल:
माना वृत्त C(0, r) की जीवा AB के सिरे A और B पर स्पर्श रेखाएँ PA और PB खींची गई हैं जो कि बिन्दु P पर काटती हैं।

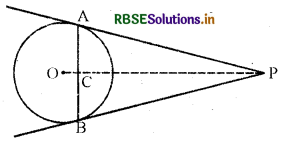
माना OP, जीवा AB को बिन्दु C पर काटती है।
सिद्ध करना है-∠PAC = ∠PBC
उपपत्ति-ΔPCA और ΔPCB में
PA = PB (बाह्य बिन्दु P से वृत्त पर स्पर्श रेखाएँ हैं)
PC = PC (उभयनिष्ठ भुजा)
∠APC = ∠BPC [∵ स्पर्श रेखाएँ PA व PB, OP के साथ समान कोण बनाती हैं।]

S-A-S सर्वांगसमता से
ΔPCA ≅ ΔPCB
⇒ ∠PAC = ∠PBC . इतिसिद्धम्

प्रश्न 5.
केन्द्र O वाले वृत्त पर बाह्य बिन्दु A से दो स्पर्श रेखाएँ AB तथा AC खींची गई हैं। सिद्ध कीजिये कि ∠BAC = 2∠OBC
अथवा
केन्द्र O वाले वृत्त पर बाह्य बिन्दु T से दो स्पर्श रेखाएँ TP तथा TQ खींची गई हैं। सिद्ध कीजिए कि ∠PTQ = 2∠OPQ है।
हल:
हमें केन्द्र 0 वाला एक वृत्त, एक बाह्य बिन्दु A तथा वृत्त पर दो स्पर्श रेखाएँ AB और AC, जहाँ B. C स्पर्श बिन्दु हैं, दिये हैं जैसा आकृति में दिखाया गया है।

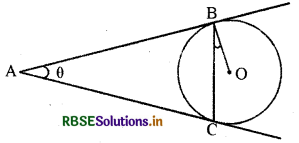
सिद्ध करना है- ∠BAC = 2∠OBC माना
∠BAC = θ
प्रमेय से हम जानते हैं कि AB = AC अतः ABC एक समद्विबाहु त्रिभुज है।
∴ ∠ABC = ∠ACB = \(\frac{1}{2}\) (180° - θ)
∠ABC = 90° - \(\frac{1}{2}\) θ
∠OBA = 90°
अतः ∠OBC = ∠OBA - ∠ABC
= 90°- (90° - \(\frac{1}{2}\)θ)
= 90° - 90° + \(\frac{1}{2}\)θ
∠OBC = \(\frac{1}{2}\)∠BAC
∠BAC = 2∠OBC इतिसिद्धम्

प्रश्न 6.
दिये गये चित्र में QS का मान ज्ञात कीजिये | जबकि दिया गया है OS = 13 cm. तथा PQ = 12 cm.

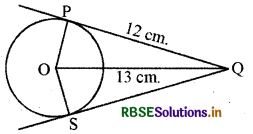
हल:
चित्रानुसार PQ एक स्पर्श रेखा है।
∴ ∠OPQ = 90°

अतः अब ΔOPQ में
(OP)² + (PQ)² = (OQ)²
(OP)² + (12)² = (13)²
(OP)² = 169 - 144 = 25
∴ OP = \(\sqrt{25}\) = 5 cm.

अर्थात् वृत्त की त्रिज्या (r) = OP = OS = 5 cm.

अब समकोण ΔOSQ से
(OS)² + (QS)² = (OQ)²
(QS) = (OQ)2² - (OS)2
= (13)² - (5)²
= 169 - 25 = 144
QS = \(\sqrt{144}\) = 12 cm.
अर्थात् QS का मान 12 cm. है।

निबन्धात्मक प्रश्न

प्रश्न 1.
चित्र में वृत्त का केन्द्र O है और स्पर्श रेखाएँ PA और PB हों, तो सिद्ध कीजिये कि AOBP एक चक्रीय चतुर्भुज है।

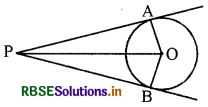
हल:
वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्दु से होकर जाने वाली त्रिज्या पर लम्बवत् होती है।
अब OA ⊥ AP और OB ⊥ BP
⇒ ∠OAP = 90° और ∠OBP = 90°
⇒ ∠OAP + ∠OBP = 90° + 90°
⇒ ∠OAP + ∠OBP = 180° .... (i)

चतुर्भुज OAPB के कोणों का योग 360° होता है।
∴ ∠APB + ∠BOA = 360° - (180°)
∠APB + ∠BOA = 180° .... (ii)

समीकरण (i) तथा (ii) से स्पष्ट है।
∠OAP + ∠OBP = 180° और ∠APB + ∠BOA = 180°
यहाँ पर सम्मुख कोणों का योग सम्पूरक है।
अतः चतुर्भुज AOBP एक चक्रीय चतुर्भुज है। (इतिसिद्धम्)

प्रश्न 2.
5 cm. त्रिज्या के एक वृत्त की 8 cm. लम्बी एक जीवा PQ है। P और Q पर स्पर्श रेखाएँ परस्पर एक बिन्दु T पर प्रतिच्छेद करती हैं ( देखिए आकृति)। TP की लम्बाई ज्ञात कीजिए।

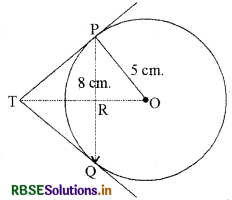
हल:
OT को मिलाएँ। माना यह PQ को बिन्दु R पर प्रतिच्छेदित करती है। तब ΔTPQ समद्विबाहु है और TO, ZPTQ का कोणार्धक है। इसलिए OT ⊥ PQ और इस प्रकार OT, PQ का अर्धक है जिससे
PR = RQ = 4 cm.

साथ ही OR = \(\sqrt{\mathrm{OP}^{2}-\mathrm{PR}^{2}}\)
= \(\sqrt{5^{2}-4^{2}}\) cm = 3 cm.

TP को पाइथागोरस प्रमेय द्वारा निम्न प्रकार से ज्ञात कर सकते हैं। माना TP = x और TR = y तो समकोण ΔPRT में
(TP)² = (TR)² + (PR)²
(x) = y² + (4)²
x² = y² + 16

समकोण ΔOPT में
(OT)² = (PT)² + (PO)²
(TR + OR)² = (x)² + (5)²
(y + 3)² = x² + 25 .... (ii)

समीकरण (i) को समीकरण (ii) में से घटाने पर
x² + 25 - x² = (y + 3)² - y² - 16
25 = y² + 6y + 9 - y² - 16
25 = 6y - 7
6y= 32
y = \(\frac{32}{6}=\frac{16}{3}\)

समीकरण (i) से

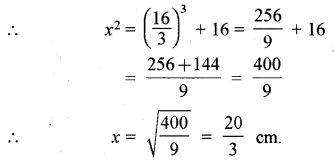
प्रश्न 3.
किसी बाह्य बिन्दु P से वृत्त पर खींची गई दो स्पर्श रेखाओं PA तथा PB पर स्थित दो बिन्दुओं L व N पर काटने वाली रेखा वृत्त के बिन्दु M पर स्पर्श करती है, तो सिद्ध करें PL + LM = PN + NM
अथवा
चित्र में PA तथा PB एक वृत्त की स्पर्श रेखाएँ हैं। वृत्त पर एक बिन्दु M हो, तो सिद्ध कीजिए कि PL + LM = PN + NM

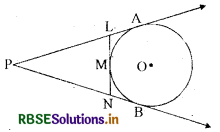
हल:
दिया है : एक वृत्त जिसका केन्द्र | है। P एक बिन्दु है जो वृत्त के बाहर है। PA व PB दो स्पर्श रेखाएँ हैं। M वृत्त पर कोई बिन्दु है। रेखाखण्ड LN बिन्दु M से गुजरता है।
सिद्ध करना है: PL + LM = PN + NM
उपपत्ति : P से वृत्त की दो स्पर्श रेखाएँ PA और PB खींची गई हैं।
∴ PA = PB
या PL + LA = PN + NB. .................(i)
LA और LM वृत्त की L बिन्दु से दो स्पर्श रेखाएँ हैं।
∴ LA = LM .... (ii)
इसी प्रकार NB = NM ....... (iii)
(i), (ii) और (iii) से
PL + LM = PN + NM (इतिसिद्धम्)

प्रश्न 4.
समकोण त्रिभुज ABC की भुजा AB को व्यास मानकर खींचा गया वृत्त कर्ण AC को P पर प्रतिच्छेद करता है। सिद्ध कीजिए कि बिन्दु P पर वृत्त की स्पर्श रेखा भुजा BC को समद्विभाजित करती है।
हल:
सिद्ध करना है : ∵ BQ = QC,
जहाँ Q, P पर खींची गई स्पर्श रेखा एवं BC का प्रतिच्छेद बिन्दु है।
रचना : BP को मिलाया।
उपपत्ति : ∵ AB वृत्त का व्यास है
∴ ∠APB = 90°
(अर्द्धवृत्त का कोण समकोण होता है।)

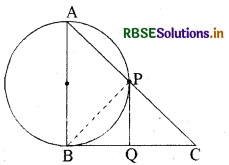
∵ ∠APB + ∠BPC = 180°
∴ 90° + ∠BPC= 180°
∴ ∠BPC = 90° .... (i)

∴ ΔABC में ∠ABC = 90°
∴ ∠BAC + ∠ACB= 90° .... (ii) (∵ त्रिभुज के तीनों कोणों का योग 180° होता है।)

समीकरण (i) तथा (ii) से
∠BPC = ∠BAC + ∠ACB
या ∠BPQ + ∠CPQ = ∠BAC + ∠ACB .... (iii)
किन्तु ∠BPQ = ∠BAC (एकान्तर वृत्त खण्ड के कोण)

∴ समीकरण (iii) से
∠CPQ = ∠ACB
∠CPQ = ∠PCQ(∵ ∠ACB = ∠PCQ)
PQ= QC .... (iv)
पुनः . PQ= QB .... (v)
(बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाएँ बराबर होती हैं।)

∴ समीकरण (iv) तथा (v) से
QC = QB
अतः PQ, BC को समद्विभाजित करती है।

प्रश्न 5.
दी गई आकृति में O एक वृत्त का केन्द्र है जिसके बाह्य बिन्दु K से वृत्त पर दो स्पर्श रेखाएँ KR, KS खींची गई हैं, तो सिद्ध कीजिए कि KR = KS.

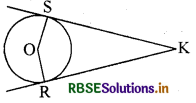
हल:
दिया है : वृत्त का केन्द्र 0 है और बाह्य बिन्दु K से दो स्पर्श रेखाएँ KR और KS हैं।

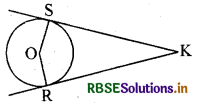
सिद्ध करना है : KR = KS.
रचना : OS, OR व OK को मिलाया।
उपपत्ति : हम जानते हैं कि स्पर्श रेखा वृत्त की त्रिज्या पर लम्बवत् होती है।
अतः ∠OSK = ∠ORK = 90° ....(i)
अब AOSK तथा AORK में
∠OSK = ∠ORK = 90° [समीकरण (i) से]
OK = OK (उभयनिष्ठ भुजा)
OS = OR (वृत्त की त्रिज्याएँ)
∴ समकोण - कर्ण - भुजा सर्वांगसमता गुणधर्म से
ΔOSK ≅ ΔORK
अतः सर्वांगसम त्रिभुजों की संगत भुजाएँ समान होंगी।
⇒ KR =KS (इतिसिद्धम्)

प्रश्न 6.
दी गई आकृति में 0 एक वृत्त का केन्द्र है जिसके बाह्य बिन्दु C से वृत्त पर दो स्पर्श रेखाएँ CA, CB खींची गई हैं, तो सिद्ध कीजिए ∠AOB व ∠ACB संपूरक हैं।

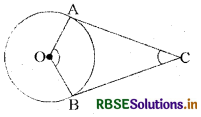
हल:
दिया है - एक वृत्त जिसका केन्द्र 0 है। C वृत्त के बाहर स्थित किसी बिन्दु C से CA और CB दिये गये वृत्त पर स्पर्श रेखाएँ हैं।

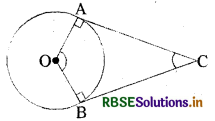
B सिद्ध करना है : ∠AOB + ∠ACB = 180°
उपपत्ति : OA त्रिज्या है और CA बिन्दु C से दिये | गये वृत्त पर स्पर्श रेखा है।
∠OAC = 90° [∵ वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्दु | से जाने वाली त्रिज्या पर लम्ब होती है।].
इसी प्रकार ∠OBC = 90° ....(ii)

अब, चतुर्भुज BOAC में,
∠BOA + ∠CBO + ∠OAC + ∠ACB = 360°
या ∠BOA + 90° + 90° + ∠ACB = 360°
या ∠BOA + ∠ACB = 360° - 180°
या ∠BOA + ∠ACB = 180° (इतिसिद्धम्)