RBSE 12th Geography Practical Book Solutions Chapter 2 आंकड़ों का प्रक्रमण

Rajasthan Board RBSE Solutions for Class 12 Geography Practical Book Chapter 2 आंकड़ों का प्रक्रमण Textbook Exercise Questions and Answers.

RBSE 12th Geography Practical Book Solutions Chapter 2 आंकड़ों का प्रक्रमण

RBSE Class 12 Geography आंकड़ों का प्रक्रमण Textbook Questions and Answers

प्रश्न 1. 
निम्नलिखित चार विकल्पों में से सही विकल्प चुनिए।
(i) केन्द्रीय प्रवृत्ति का जो माप चरम मूल्यों से प्रभावित नहीं होता है, वह है।
(क) माध्य
(ख) माध्य तथा बहलक 
(ग) बहुलक
(घ) माध्यिका। 
उत्तर:
(ग) बहुलक

(ii) केन्द्रीय प्रवृत्ति का वह माप जो किसी वितरण के उभरे भाग से हमेशा संपाती होगा, वह है।
(क) माध्यिका
(ख) माध्य तथा बहुलक 
(ग) माध्य
(घ) बहुलक। 
उत्तर:
(ग) माध्य

(iii) ऋणात्मक सह - सम्बन्ध वाले प्रकीर्ण अंकन में अंकित मानों के वितरण की दिशा होगी।
(क) ऊपर बाएँ से नीचे दाएँ
(ख) नीचे बाएँ से ऊपर दाएँ 
(ग) बाएँ से दाएँ
(घ) ऊपर दाएँ से नीचे बाएँ।
उत्तर:
(क) ऊपर बाएँ से नीचे दाएँ

 

प्रश्न 2. 
निम्नलिखित प्रश्नों के उत्तर लगभग 30 शब्दों में दीजिए।
(i) माध्य को परिभाषित कीजिए।
उत्तर:
माध्य वह मान है जो सभी मूल्यों के योग को कुल पदों की संख्या से विभाजित करके प्राप्त किया जाता है। दूसरे शब्दों में, किसी चर के विभिन्न मूल्यों का साधारण अंकगणितीय औसत माध्य कहलाता है।

(ii) बहुलक के उपयोग के क्या लाभ हैं? 
उत्तर:
बहुलक एक सरल व लोकप्रिय माध्य है, जिससे 'अक्सर', 'प्रायः' या 'अधिकतर' का बोध होता है। समान्तर माध्य के विपरीत बहुलक पर समंक - श्रेणी के चरम - मूल्यों का कोई प्रभाव नहीं पड़ता। दूसरे शब्दों में, बहुलक के द्वारा केवल उस मूल्य का पता चलता है जिसकी आवृत्ति सबसे अधिक है। दैनिक जीवन व व्यापारिक क्रिया-कलापों के अलावा किसी वस्तु के उत्पादन तथा मौसम आदि का पूर्वानुमान लगाने में इसका काफी प्रयोग होता है।

(iii) अपकिरण किसे कहते हैं?
उत्तर:
किसी समंक: श्रेणी के विभिन्न व्यक्तिगत मूल्यों का श्रेणी के माध्य से औसत अन्तर या विचलन अपकिरण कहलाता है। अपकिरण के द्वारा यह ज्ञात करते हैं कि कोई सांख्यिकीय माध्य किस सीमा तक सम्बन्धित समंक-श्रेणी का प्रतिनिधित्व करता है। अपकिरण मान के द्वारा माध्य के दोनों ओर व्यक्तिगत मूल्यों के फैलाव की प्रकृति को समझना आसान हो जाता है।

(iv) सह - सम्बन्ध को परिभाषित कीजिए।
उत्तर:
दो या दो से अधिक चरों के मध्य साहचर्य की प्रकृति एवं गहनता को सह-सम्बन्ध कहते हैं। दूसरे शब्दों में, जब कोई दो चर मूल्य परस्पर एक दिशा में या विपरीत दिशा में घटने - बढ़ने की प्रवृत्ति रखते हैं तो ऐसी स्थिति में उनके मध्य एक विशेष प्रकार का सम्बन्ध पाया जाता है। इस सम्बन्ध को ही सहसम्बन्ध कहा जाता है।

(v) पूर्ण सह - सम्बन्ध किसे कहते हैं?
उत्तर:
जब दोनों चरों का मान + 1 होता है (धनात्मक या ऋणात्मक) तो उसे पूर्ण सह-सम्बन्ध कहते हैं। इसमें सभी बिन्दु एक सरल रेखा पर स्थित होते हैं। जब सरल रेखा प्रकीर्ण आरेख के निचले बाएँ किनारे से ऊपरी दाएँ भाग की ओर जाती है, तो पूर्ण धनात्मक सह - सम्बन्ध (+1.00) कहलाता है। इसके विपरीत जब सरल रेखा प्रकीर्ण आरेख के ऊपरी बाएँ भाग से निचले दाएँ भाग की ओर जाती है तो पूर्ण ऋणात्मक सह - सम्बन्ध (-1.00) कहलाता है।

(vi) सह-सम्बन्ध की अधिकतम सीमाएँ क्या हैं?
उत्तर:
सह-सम्बन्ध की अधिकतम सीमा 1 होती है। सह-सम्बन्ध का विस्तार -1 से शून्य की ओर होते हुए +1 तक होता है। इसका मान किसी भी परिस्थिति में एक (1) से अधिक नहीं हो सकता।

प्रश्न 3. 
निम्नलिखित प्रश्नों के उत्तर लगभग 125 शब्दों में दीजिए।
(i) आरेखों की सहायता से सामान्य तथा विषम वितरणों में माध्य, माध्यिका तथा बहुलक की सापेक्षिक स्थितियों की व्याख्या कीजिए। 
उत्तर:
सामान्य वितरण वक्र के माध्यम से केन्द्रीय प्रवृत्ति के तीनों मापों माध्य, माध्यिका तथा बहुलक की व्याख्या की जा सकती है। सामान्य वक्र आवृत्तियों का ऐसा वितरण होता है जिसका रेखा चित्र घंटाकार वक्र कहलाता है।


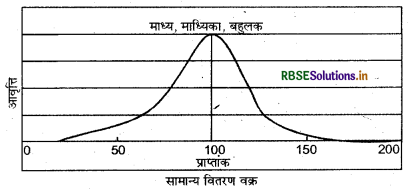
बौद्धिकता, व्यक्तित्व तथा विद्यार्थियों की उपलब्धि के समंक जैसी अनेक मानवीय विशेषताओं का सामान्य वितरण होता है। सामान्य वितरण वक्र सममित होता है। दूसरे शब्दों में, इसमें अधिकांश प्रेक्षण श्रेणी के मध्यमान पर अथवा आस-पास एकत्रित होते हैं। जैसे-जैसे दूरस्थ मान की ओर बढ़ते हैं, पर्यवेक्षित प्रेक्षणों की संख्या सममित रूप से घटती जाती है। सामान्य वितरण को वक्र के माध्यम से दर्शाया गया है।

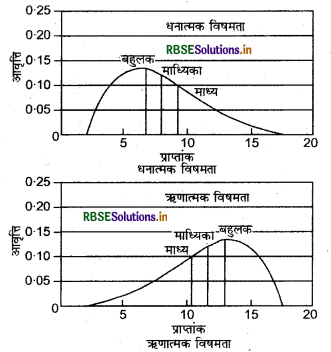
सामान्य वितरण में माध्य: माध्यिका तथा बहुलक का मान समान होता है क्योंकि सामान्य वितरण सममित होता है। अधिकतर इकाइयाँ वितरण के मध्य में अथवा माध्य के निकट होती हैं। इस प्रकार यदि आँकड़े किसी प्रकार विषम स्थिति में हो तो माध्य, माध्यिका तथा बहुलक समान नहीं होंगे। विषम आँकड़ों के वितरण का प्रभाव धनात्मक तथा ऋणात्मक दोनों होता है, जिसे निम्न चित्र के द्वारा दर्शाया जा सकता है।

प्रश्न 2.
माध्य, माध्यिका तथा बहुलक की उपयोगिता पर टिप्पणी कीजिए (संकेत : उनके गुण तथा दोषों से)।
उत्तर:
माध्य की उपयोगिता: किसी सांख्यिकीय विधि की उपयोगिता उसके गुण तथा दोषों के तुलनात्मक महत्व पर निर्भर करती है। माध्य में अनेक गुण होते हैं।

1. इसकी गणना विधि सरल है तथा सामान्य व्यक्ति भी आसानी से समझ सकता है। 
2. इसके परिकलन में श्रेणी के समस्त पदों का प्रयोग किया जाता है। 
3. इसके परिकलन में किसी प्रकार के अनुमान का प्रयोग नहीं होता अर्थात् यह निश्चयात्मक होता है। 
4. किसी निश्चित श्रेणी का माध्य सर्वथा एक ही होता है। 
5. सांख्यिकीय विश्लेषण की अन्य विधियों; जैसे-अपकिरण, विषमता व सह-सम्बन्ध में इसका बहुत अधिक प्रयोग होता।
6. इसके आधार पर समूह की तुलना आसानी से की जा सकती है।

 
माध्य के दोष: इसकी गणना में श्रेणी के समस्त पदों का उपयोग किया जाता है, जो कभी-कभी त्रुटिपूर्ण सिद्ध होता है, क्योंकि माध्य पर आँकड़ों के उच्चतम एवं न्यूनतम मानों का प्रभाव पड़ता है, जिससे कभी-कभी यह श्रेणी के समस्त पदों का प्रतिनिधित्व नहीं कर पाता है। माध्य केवल निरपेक्ष मूल्यों का औसत निकालने में उपयोगी है। अनुपात व प्रतिशत के अध्ययन में माध्य सर्वथा अनुपयुक्त होता है।
माध्यिका की उपयोगिता-माध्यिका में अनेक गुण होते हैं।

1. माध्यिका सुपरिभाषित होती है तथा इस पर चरम मानों (उच्चतम एवं निम्नतम) का प्रभाव नहीं पड़ता है। 
2. इसको सरलतापूर्वक ज्ञात किया जा सकता है। 
3. इसका प्रयोग नाभिक क्रमसूचक, अन्तराल एवं आनुपातिक सभी प्रकार के मापन मापक पर कर सकते हैं। 
4. इसे बारम्बारता वक्र पर प्रदर्शित कर सकते हैं।

माध्यिका के दोष: माध्यिका की गणना में श्रेणी के समस्त पदों के संख्यात्मक मान का योगदान सम्भव नहीं होता है जिससे माध्यिका से श्रेणी के अन्य मानों का कोई अनुमान नहीं लगा सकते हैं। अतः माध्यिका श्रेणी के समस्त पदों का पूर्णतया प्रतिनिधित्व नहीं कर पाती है।
बहुलक की उपयोगिता: बहुलक के अनेक गुण हैं। 

1. यह सबसे सरल माध्य है, जिससे 'अक्सर', 'प्रायः' या 'अधिकतर' आदि का बोध होता है। 
2. इस पर श्रेणी के उच्चतम एवं निम्नतम् मानों का प्रभाव नगण्य होता है। 
3. इसे बारम्बारता वक्र के माध्यम से भी ज्ञात किया जा सकता है। 
4. हवाओं की दिशा, आँधी, तूफान आदि भौगोलिक तथ्यों के विश्लेषण में यह परम उपयोगी सिद्ध होता है।

बहुलक के दोष-बहुलक का सबसे बड़ा दोष यह है कि यह समंक श्रेणी के सभी मूल्यों का प्रतिनिधित्व नहीं करता। अतः कभी - कभी बहुलक के आधार पर निकाला गया कोई निष्कर्ष भ्रामक हो सकता है। सम्पूर्ण समंक श्रेणी पर आधारित न होने के कारण इस माध्य का सांख्यिकीय विश्लेषण की अन्य विधियों में बहुत कम प्रयोग होता है।

प्रश्न 3.
एक काल्पनिक उदाहरण की सहायता से मानक विचलन के गणना की प्रक्रिया समझाइए।
उत्तर:
मानक विचलन: प्रकीर्णन के माप के रूप में मानक विचलन (S.D.) सबसे अधिक प्रचलित माप है। यह श्रेणी के समस्त माध्य से निकाले गये विचलनों के मध्य का धनात्मक वर्गमूल होता है। मानक विचलन प्रकीर्णन का सर्वाधिक स्थिर माप है।
मानक विचलन की गणना निम्न प्रकार से की जाती है अवर्गीकृत आँकड़ों के लिए मानक विचलन की गणना-इसके लिए निम्न सूत्र का प्रयोग होता है।
\(\sigma=\sqrt{\frac{\Sigma d^{2}}{\mathrm{~N}}}\)
जहाँ, = मानक विचलन
σ  = किसी श्रेणी के माध्य का प्रत्येक मूल्य से अन्तर अर्थात् (X - X) विचलन
∑d² = विचलनों के वर्गों का योग
N = पदों की संख्या
उदाहरण: निम्नांकित मूल्यों के लिए मानक विचलन की गणना कीजिए।
03, 05, 07, 09, 11
तालिका : मानक विचलन की गणना
हल x̅  \(=\frac{\Sigma x}{N}\)
 = 35/5 = 7
\(\begin{aligned} \sigma &=\sqrt{\frac{\Sigma d^{2}}{\mathrm{~N}}} \\ &=\sqrt{\frac{40}{5}} \end{aligned}\)
= \(\sqrt{8}\) = 2.83
σ   = 2.83
वर्गीकृत आँकड़ों के लिए मानक विचलन की गणना-इसके लिए निम्नांकित सूत्र का प्रयोग किया जाता है
\(\sigma=i \times \sqrt{\frac{\Sigma f x^{\prime 2}}{\mathrm{~N}}-\left(\frac{\Sigma f x^{\prime}}{\mathrm{N}}\right)^{2}}\)
जहाँ,  σ  = मानक विचलन
X = कल्पित माध्य से पद विचलन
f = आवृत्ति 
i = वर्ग विस्तार
N = आवृत्ति का कुल योग अर्थात् ∑f
उदाहरण: निम्नलिखित आँकड़ों के लिए मानक विचलन की गणना कीजिए
\(\begin{aligned} &\sigma=i \times \sqrt{\frac{\Sigma f x^{\prime 2}}{N}-\left(\frac{\Sigma f x^{\prime}}{N}\right)^{2}} \\ &\sigma=10 \times \sqrt{\frac{142}{50}-\left(\frac{6}{50}\right)^{2}} \end{aligned}\)
\(\sigma=10 \times \sqrt{2 \cdot 84-(0 \cdot 12)^{2}}\)
\(\begin{aligned} &=10 \times \sqrt{2 \cdot 84-0 \cdot 0144} \\ &=10 \times \sqrt{2 \cdot 8256} \end{aligned}\)
10 x 6.81 = 1.681
σ = 16.81

प्रश्न 4.
प्रकीर्णन का कौन-सा माप सबसे अधिक अस्थिर है तथा क्यों?
उत्तर:
केवल केन्द्रीय प्रवृत्ति के माप ही वितरण को उचित रूप से वर्णित नहीं करते क्योंकि वे केवल वितरण का केन्द्र ही चिर्चा त करते हैं। इससे यह मालूम नहीं हो पाता है कि विभिन्न मूल्य या माप केन्द्र के परिप्रेक्ष्य में किसी प्रकार प्रकीर्णित है। इसलिए वितरण का श्रेष्ठतर प्रतिरूप प्राप्त करने के लिए प्रकीर्णन या बिखराव के माप की आवश्यकता होती है। प्रकीर्णन से तात्पर्य केन्द्रीय प्रवृत्ति के माप से इकाइयों के बिखराव से लगाया जाता है। यह माप औसत मूल्य से किसी इकाई अथवा संख्यात्मक मान की विषमता या बिखराव की प्रवृत्ति का मापन करता है।

प्रकीर्णन के मापन की कई विधियाँ हैं; जैसे-विस्तार, चतुर्थक विचलन, माध्य विचलन, मानक विचलन तथा विचरण गुणांक एवं लारेंज वक्र आदि। लेकिन इसमें विस्तार, मानक विचलन तथा विचरण गुणांक प्रकीर्णन के सर्वाधिक प्रचलित माप हैं। प्रकीर्णन के माप के रूप में सर्वाधिक अस्थिर माप विस्तार है, जबकि अन्य माप में इतनी अस्थिरता नहीं दिखाई देती है। अतः विस्तार (Range) को इस प्रकार समझा जा सकता है।

विस्तार-किसी श्रेणी में अधिकतम व न्यूनतम मूल्य के बीच के अन्तर को विस्तार (Range) कहते हैं। यह किसी श्रेणी में सबसे छोटे माप और सबसे बड़े माप के बीच का अन्तर होता है। इस प्रकार विस्तार केवल चरम मानों (अधिकतम एवं न्यूनतम मूल्य) पर ही आधारित होता है। अधिकतम मूल्य अथवा न्यूनतम मूल्य में जैसे ही कोई परिवर्तन होता है, उसके साथ-साथ विस्तार मूल्य भी परिवर्तित हो जाता है। इसी कारण विस्तार किसी भी श्रेणी के विचरण का स्थायी मापन नहीं होता है अर्थात् यह अस्थिर माप होती है। इसे निम्न उदाहरण के द्वारा स्पष्ट किया जा सकता है।

उदाहरण: निम्नलिखित दैनिक मजदूरी के वितरण के लिए विस्तार की गणना कीजिए।
40, 42, 44, 46, 50, 54, 56,58, 60, 100
हल - विस्तार (Range) = Largest (अधिकतम) - Smallest (न्यूनतम)
R = L - S
अतः
R = 100 - 40 = 60
यदि उपरोक्त वितरण में से 10वें मूल्य को हटा दें तो R का मान 20 (60 - 40) हो जायेगा। श्रेणी से केवल एक मूल्य हटाने पर R का मान मात्र एक तिहाई रह गया है। अतः स्पष्ट है कि प्रकीर्णन के माप के रूप विस्तार (R) का मान दो चरम मूल्यों पर आधारित है, जो अत्यधिक अस्थिर है।

प्रश्न 5.
सह - सम्बन्ध की गहनता पर एक विस्तृत टिप्पणी लिखिए।
उत्तर:
सह - सम्बन्ध की गहनता: सह - सम्बन्ध से तात्पर्य दो चरों के मध्य अनुरूपता अथवा साहचर्य की प्रकृति एवं गहनता से है। प्रकृति तथा गहनता का आशय दिशा एवं मात्रा से है, जिसके अनुरूप दो चर परस्पर विचरण करते हैं। सह-सम्बन्ध की दिशा ऋणात्मक या धनात्मक हो सकती है। दोनों चरों में साहचर्य की गहनता अधिकतम् 1 (एक) तक होती है। इसका अधिकतम विस्तार -1 से शून्य होते हुए +1 तक होता है। किसी भी स्थिति में सह-सम्बन्ध का मान एक से अधिक नहीं हो सकता। सह-सम्बन्ध पूरा + 1 (एक) होने पर (ऋणात्मक या धनात्मक) इसे पूर्ण सह-सम्बन्ध कहते हैं। गहनतम सह-सम्बन्ध के दो विपरीत सिरों के ठीक मध्य में शून्य (0) सह-सम्बन्ध स्थित होता है, जिस बिन्दु पर चरों के मध्य सह-सम्बन्ध का अभाव होता है। सह-सम्बन्ध की दिशा व गहनता को निम्न रेखा चित्र के माध्यम से समझा जा सकता है


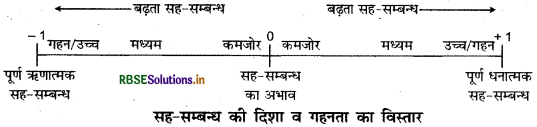
पूर्ण धनात्मक सह: सम्बन्ध का अभाव सह - सम्बन्ध चित्र - सह - सम्बन्ध की दिशा व गहनता का विस्तार पूर्ण धनात्मक सह-सम्बन्ध-उपर्युक्त रेखा चित्र से स्पष्ट है कि जब इस प्रकार के युग्म के मानों को अंकित किया जाता है तो सभी बिंदु एक सरल रेखा पर स्थित होते हैं । जब यह सरल रेखा प्रकीर्ण आरेख के निचले बाएँ से ऊपरी दाएँ भाग की ओर जाती है तो उसे पूर्ण धनात्मक सह-सम्बन्ध कहते हैं।

पूर्ण ऋणात्मक सह: सम्बन्ध - जब एक सरल रेखा पर स्थित सभी बिन्दु प्रकीर्ण आरेख के ऊपरी बाएँ से निचले दाएँ भाग की ओर जाते हैं तो उसे पूर्ण ऋणात्मक सह - सम्बन्ध कहते हैं।

शून्य सह - सम्बन्ध: जब दोनों चरों के मध्य परिवर्तन का कोई प्रभाव नहीं होता है, तो उसे शून्य सह-सम्बन्ध या सह-सम्बन्ध का अभाव कहा जाता है। अन्य सह-सम्बन्ध-पूर्ण सह-सम्बन्ध (+ 1) व शून्य सह-सम्बन्ध के मध्य में साहचर्य की सामान्य परिस्थितियाँ पायी जाती हैं, जिन्हें कमजोर मध्यम तथा गहन सह-सम्बन्ध कहा जाता है। प्रकीर्णन या बिखराव अधिक होने पर सह-सम्बन्ध कमजोर तथा प्रकीर्णन कम होने पर सह-सम्बन्ध गहन होता है।

प्रश्न 6.
कोटि सह-सम्बन्ध की गणना के विभिन्न चरण कौन - कौन से हैं?
उत्तर:
कोटि सह - सम्बन्ध की गणना: कोटियों के आधार पर सहसम्बन्ध की गणना विधि का प्रतिपादन स्पीयरमैन द्वारा किया गया था। इसी कारण इसे स्पीयरमैन के कोटि सह-सम्बन्ध के नाम से भी जाना जाता है। इसे ग्रीक अक्षर p से लिखते हैं, जिसका उच्चारण, रो rho है। कोटि सह-सम्बन्ध की गणना के विभिन्न चरण होते हैं।
कोटि सह: सम्बन्ध की गणना के विभिन्न चरण:

1. दिए गये X तथा Y चरों के आँकड़ों को तालिका के प्रथम व द्वितीय स्तम्भों में उतार लिया जाता है।
2. दोनों चरों की अलग - अलग कोटियाँ निर्धारित की जाती हैं। X - चर की कोटियों को XR शीर्षक से तृतीय स्तम्भ में तथा y - चर की कोटियों को YR शीर्षक से चतुर्थ स्तम्भ में अंकित किया जाता है। आँकड़ों में उच्चतम मान को कोटि एक तथा न्यूनतम मान को अन्तिम कोटि (कुल इकाइयों की संख्या के बराबर) आवंटित किया जाता है।
3. XR तथा YR के निर्धारण के पश्चात् दोनों कोटियों में अंतर निकाला जाता है। इसका उल्लेख पाँचवें स्तम्भ में करते हैं। इसमें धनात्मक और ऋणात्मक चि का प्रयोग नहीं करते हैं, क्योंकि अगले चरण में अन्तरों का वर्ग निकालने के कारण धनात्मक अथवा ऋणात्मक चिों का महत्व समाप्त हो जाता है।
4. प्रत्येक अन्तर का वर्ग ज्ञात करके उनका योग किया जाता है। इसे छठे स्तम्भ में लिखा जाता है। 
5. कोटि सह - सम्बन्ध की गणना निम्नांकित सूत्र के आधार पर की जाती है

\(\rho=1-\frac{6\left[\Sigma D^{2}\right]}{N^{3}-N}\)

जहाँ, p = कोटि सह-सम्बन्ध, 
D = X तथा Y की कोटियों का अन्तर
∑D² == दोनों कोटियों के अन्तर के वर्ग का योग
N = X, Y चरों की संख्या 
उदाहरण:
निम्नलिखित आँकड़ों के द्वारा स्पीयरमैन के कोटि सह-सम्बन्ध की गणना कीजिए

गणित में प्राप्तांक (X)	02	08	0	20	12	16	06	18	09	10
विज्ञान में प्राप्तांक (Y)	04	12	6	24	16	18	08	20	09	1

तालिका - स्पीयरमैन के कोटि सह-सम्बन्ध की गणना:

1 X	2 Y	3 XR	4 YR	5 D	6 D2
2 8 0 12 20 16 78 9 10	4 12 6 24 16 18 8 20 9	9 7 10 1 4 3 8 2 6	10 5 9 1 4 3 8 2 7	1 2 1 0 0 0 0 1 1	1 4 1 0 0 0 0 1 1
N = 10					D2 = 8

∑ D² = 8

N = 10
\(\rho=1-\frac{6 \Sigma D^{2}}{N\left(N^{2}-1\right)}\)

\(=1-\frac{6 \times 8}{10\left(10^{2}-1\right)}=1-\frac{48}{10(99)}\)

\(=1-\frac{48}{990}\) = 1 - 0.05 = 0.95

सह - सम्बन्ध (p) = 0.957 
इस प्रकार कोटि सह-सम्बन्ध की गणना के आधार पर दोनों चरों के मध्य गहन धनात्मक सह-सम्बन्ध है।

क्रियाकलाप:

प्रश्न 1.
भौगोलिक विश्लेषण के लिए प्रयुक्त कोई काल्पनिक उदाहरण लीजिए तथा अवर्गीकृत आँकड़ों की माध्य गणना करने की प्रत्यक्ष व अप्रत्यक्ष विधियों को समझाइये।
उत्तर:
उदाहरण: निम्नलिखित सारणी में दौसा जिले के मासिक तापमान के आँकड़े दिये गये हैं। इससे दौसा जिले का औसत तापमान ज्ञात कीजिए।

माह	जनवरी	फरवरी	मार्च	अप्रैल	मई	जून	जुलाई	अगस्त	सितम्बर	अक्टूबर	नवम्बर	दिसम्बर
तापमान	13	16	21	27	32	34	31	30	28	27	20	14

 

माह	तापमान तापमान (डिग्री सेल्सियस में)	अप्रत्यक्ष विधि d = 0 - 8
जनवरी फरवरी मई जून जुलाई अगस्त सितम्बर अक्टूबर नवम्बर दिसम्बर	13 16 21 27 31 32 34 31 30 28 27 20 14	3 6 11 17 22 24 21 20 18 17 10 4 12
∑X ∑d	293	173
\(\frac{\Sigma x}{N}\) व \(\frac{\Sigma d}{\mathrm{~N}}\)	\(\frac{293}{12} \) = 14.12	173/12 = 14.41

जहाँ 10 कल्पित माध्य है। d कल्पित माध्य से विचलन है।
प्रत्यक्ष विधि से माध्य की गणना-प्रत्यक्ष विधि द्वारा माध्य की गणना करने के लिए पर्यवेक्षण के सभी मूल्यों को जोड़कर पदों की कुल संख्याओं से भाग दे दिया जाता है। अवर्गीकृत आँकड़ों से माध्य की गणना के लिए निम्नांकित सूत्र का प्रयोग किया जाता है।
x̅ = \(\frac{\Sigma x}{\mathrm{~N}}\)
x̅ = 293/12
= 24.41
जहाँ, x̅ = माध्य
∑x̅ = सभी मूल्यों का कुल योग 
N = श्रेणी में कुल पदों की संख्या
अप्रत्यक्ष विधि से माध्य की गणना: श्रेणी में प्रेक्षणों की संख्या अधिक होने से अप्रत्यक्ष विधि से माध्य की गणना की जाती है। इस विधि में एक कल्पित माध्य मानकर संख्याओं के विस्तार को कम कर देते हैं। इस प्रकार घटाए गये मूल्यों के आधार पर माध्य को गणना की जाती है। अप्रत्यक्ष विधि से माध्य की गणना के लिए निम्नांकित सूत्र का प्रयोग किया जाता है।

\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma d}{\mathrm{~N}}\)
जहाँ, A = घटाया हुआ स्थिरांक या कल्पित माध्य
∑d = स्थिरांक घटाए हुए मूल्यों का कुल योग या कल्पित माध्य से विचलन का कुल योग
N = कुल पदों की संख्या . इस प्रकार,
x̅ = 10 + 173/12
= 10 + 14.41
माध्य (x̅) =24:41 

प्रश्न 2.
विभिन्न प्रकार के पूर्ण सह-सम्बन्ध दर्शाने के लिए प्रकीर्ण।
उत्तर:
पूर्ण धनात्मक सह: सम्बन्ध-जब सरल रेखा प्रकीर्ण आरेख के निचले बायें से ऊपरी दायें भाग की ओर जाती है, तो यह पूर्ण धनात्मक सह - सम्बन्ध कहलाता है। इसमें X - अक्ष पर प्रत्येक एक इकाई की वृद्धि के साथ-साथ Y - अक्ष पर भी दो इकाइयों की वृद्धि हो जाती है। पूर्ण धनात्मक सह - सम्बन्ध का मान +1.00 होता है।

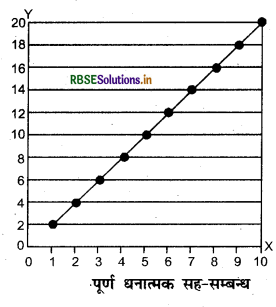
पूर्ण ऋणात्मक सह: सम्बन्ध - जब सरल रेखा प्रकीर्ण आरेख के ऊपरी बाएँ भाग से निचले दाएँ भाग की ओर जाती है, तो यह पूर्ण ऋणात्मक सह-सम्बन्ध कहलाता है, जिसका मान -1.00 होता है। इसमें X -अक्ष पर प्रत्येक एक इकाई वृद्धि के साथ-साथ Y -अक्ष पर दो इकाइयों की कमी हो जाती है। इसका आशय यह है कि दोनों चरों में एक - दूसरे के विपरीत गति करने की प्रवृत्ति है, अर्थात् एक चर में वृद्धि होने से दूसरे चर में कमी होती है।

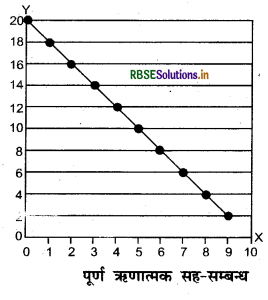
शून्य सह-सम्बन्ध: जब युग्म के दोनों चर एक-दूसरे में परिवर्तन का कोई प्रत्युत्तर नहीं देते, तो ऐसी स्थिति में दोनों चरों के मध्य कोई सह-सम्बन्ध नहीं होता है। इसे शून्य सह-सम्बन्ध अथवा सह-सम्बन्ध का अभाव कहते हैं। X -चर में परिवर्तन का Y-चर द्वारा प्रत्युत्तर नहीं दिये जाने के कारण शून्य सह-सम्बन्ध को प्रकीर्ण अंकन-A द्वारा प्रदर्शित किया गया है। इसी तरह Y-चर में परिवर्तन का X -चर द्वारा कोई प्रत्युत्तर नहीं दिये जाने के कारण प्रकीर्ण अंकन-B में भी शून्य सह-सम्बन्ध की स्थिति उत्पन्न हुई है।

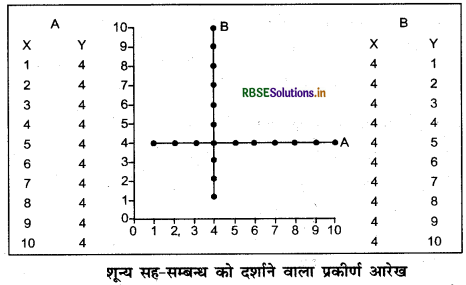
कमजोर, मध्यम तथा गहन सह-सम्बन्ध-पूर्ण सह-सम्बन्ध \((\pm 1)\) व शून्य सह-सम्बन्ध के बीच साहचर्य की सामान्य प्रवृत्ति पायी जाती है, जिन्हें कमजोर, मध्यम व गहन सह-सम्बन्ध कहा जाता है। इन तीनों स्थितियों को निम्न चित्र द्वारा दर्शाया गया है। इनमें अंकित बिन्दुओं को देखकर कहा जा सकता है कि प्रकीर्णन या बिखराव जितना अधिक होगा, सह-सम्बन्ध उतना ही कमजोर होगा तथा प्रकीर्णन कम होने से सह-सम्बन्ध गहन होगा।