RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 9 Algebraic Expressions and Identities Intext Questions

(Try These Page No: 138)

Question 1.
Give five examples of expressions containing one variable and five examples of expressions containing two variables.
Answer:
Five examples of expressions containing one variable may be x + 7, x - 7, 6 + y, 8 - y and 5 + 4x.
Five examples of expressions containing two variables may be x + 5y, x - 5y, 6x + y, 8x - y and 4x + 5y.

Question 2.
Show on the number line x, x - 4, 2x + 1, 3x - 2.
Answer:
Representation of expression x

Representation of expression x - 4

Representation of expression 2x + 1

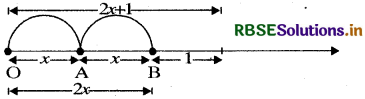
Representation of expression 3x - 2

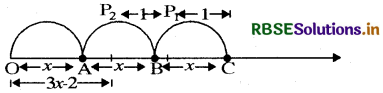
(Page No: 138)

Question 1.
Identify the coefficient of each term in the expression x²y² - 10x²y + 5xy² - 20.
Answer:
Here,
The coefficient of x²y² = 1
The coefficient of x²y = - 10
The coefficient of xy² = 5

(Page No: 138)

Question 1.
Classify the following polynomials as monomials, binomials, trinomials. - z + 5, x + y + z, y + z + 100, ab - ac, 17
Answer:
The given polynomials are classified as under-
Monomials : 17
Binomials : - z + 5, ab - ac
Trinomials : x + y + z, y + z + 100

Question 2.
Construct
(a) 3 binomials with only x as a variable;
Answer:
3 binomials with only x as a variable may be 5x + 3, 9x + 8, 6 - x

(b) 3 binomials with x and y as variables;
Answer:
3 binomials with x and y as variable may be 3x + 4y, xy - 7, 5x - y.

(c) 3 monomials with x and y as variables;
Answer:
3 monomials with x and y as variables may be xy, 6x²y, - 3xy²

(d) 2 polynomials with 4 or more terms.
Answer:
2 polynomials with 4 or more terms may be 3x³ - x² + 7x + 3, 8 - 5x.

(Try These - Page No: 139)

Question 1.
Write two terms which are like—
(i) 7xy
(ii) 4mn²
(iii) 2l
Answer:
(i) Two terms which are like 7xy may be 5xy, - 3xy.
(ii) Two terms which are like 4mn² may be 3mn², - 4n²m.
(iii) Two terms which are like 2l may be 3l, - 4l.

(Try These Page No: 142)

Question 1.
Can you think of two more such situations, where we may need to multiply algebraic expression.
[Hint : % Think of speed and time;
Think of interest to be paid, the principal and the rate of simple interest; etc.]
Answer:
(i) Distance = Speed × Time
(ii) Simple interest
= \(\frac{\text { Principal } \times \text { Rate } \times \text { Time }(y r s)}{100}\)
= \(\frac{P \times R \times T}{100}\)

(Try These Page No: 143)

Question 1.
Find 4x × 5y × 7z
First find 4x × 5y and multiply it by 7z; or
first find 5y × 7z and multiply it by 4x.
Is the result the same? What do you observe?
Does the order in which you carry out the multiplication matter?
Answer:
We have
4x × 5y × 7z = (4x × 5y) × 7z
= 20xy × 7z = 140xyz
and 4x × 5y × 7z = 4x × (5y × 7z)
= 4x × 35yz = 140xyz
∴ (4x × 5y) × 7z = 4x × (5y × 7z) i.e. the results remain same.
∴ The multiplication of monomials is associative, i.e. the order in which we carry out the multiplication does not matter.

(Try These Page No: 144)

Question 1.
Find the product
(i) 2x(3x + 5xy)
(ii) a²(2ab - 5c)
Answer:
(i) 2x(3x + 5xy) = 2x × 3x + 2x × 5xy
= 6x² + 10x²y

(ii) a²(2ab - 5c) = q² × 2ab - a² × 5c
= 2a³b - 5a²c

(Page No: 145)

Question 1.
Find the product—
(4p² + 5p + 7) × 3p
Answer:
(4p² + 5p + 7) × 3p = 4p² × 3p + 5p × 3p + 7 × 3p
= 12p³ + 15p² + 21p

(Try These Page No: 149)

Question 1.
Put - b in place of b in identity (I). Do you get identity (II)?
Answer:
Putting b = - b in (a + b)² = a² + 2ab + b², we get
{a + (- b)}² = a² + 2a(- b) + (- b)²
⇒ (a - b)² = a² - 2 ab + b²
Thus we obtain the identity II from identity I on putting b = - b.

(Page No: 149)

Question 1.
Verify identity IV, for a = 2, b = 3, x = 5 {IV : (x + a) (x + b) = x² + (a + b) x + ab]
Answer:
for a = 2, b = 3, x = 5 we have
LHS = (5 + 2) (5 + 3) = (7) (8) = 56
RHS = (5)² + (2 + 3) (5) + (2) (3)
= 25 + 25 + 6 = 56
Thus, the values of the two sides of the equality are equal for a = 2, b = 3, x = 5.

Question 2.
Consider the special case of identity (IV) with a = b, what do you get? Is it related to Identity (I)?
Answer:
When a = b the identity (IV) becomes
(x + a) (x + a) = x² + (a + a)x + aa
⇒ (x + a)² = x² + 2 ax + a²
Yes, it is related to identity I.

Question 3.
Consider the special case of identity (IV) with a = - c and b = - c. What do you get? Is it related to identity (II)?
Answer:
When a = - c and b = - c, then identity (IV) becomes
{x + (- c)} {x + (- c)} = x² + (- c - c)x + (- c) (- c)
⇒ (x - c) (x - c) = x² + (- 2c)x + c²
⇒ (x - c)² = x² - 2cx + c²
Yes, it is related to identity II.

Question 4.
Consider the special case of identity (IV) with b = - a. What do you get? Is it related to identity (III)?
Answer:
When b = - a, the identity (IV) becomes
(x + a) {x + (- a)} = x² + (a - a)x + (a)(- a)
⇒ (x + a) (x - a) = x² - a²
Yes, it is related to identity (III).