RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 Textbook Exercise Questions and Answers.

Rajasthan Board RBSE Solutions for Class 8 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 8. Students can also read RBSE Class 8 Maths Important Questions for exam preparation. Students can also go through RBSE Class 8 Maths Notes to understand and remember the concepts easily. Practicing the class 8 maths chapter 6 try these solutions will help students analyse their level of preparation.

RBSE Class 8 Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.5

Question 1.
Use a suitable identity to get each of the following products—
(i) (x + 3) (x + 3)
Answer:
(x + 3) (x + 3) = x2 + (3 + 3)x + (3) (3)
[Using (x + a) (x + b) = x2 + (a + b)x + ab]
= x2 + 6x + 9
or (x + 3) (x + 3) = (x + 3)2
= x2 + 2(3)x + (3)2
[Using (a + b)2 = a2 + 2ab + b2]
= x2 + 6x + 9

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(ii) (2y + 5) (2y + 5)
Answer:
(2y + 5) (2y + 5)= (2y)2 + (5 + 5) (2y) + (5)(5)
[Using (x + a) (x + b) = x2 + (a + b)x + ab]
= 4y2 + 20y + 25 or (2y + 5) (2y + 5)
= (2y + 5)2
= (2y)2 + 2(2y) (5) + (5)2
[Using (a + b)2 = a2 + 2ab + b2]
= 4y2 + 20y + 25

(iii) (2a - 7) (2a- 7)
Answer:
(2a - 7) (2a - 7) = (2a - 7)2
= (2a)2 - 2(2a) (7) + (7)2.
[Using (a - b)2 = a2 - 2ab + b2]
= 4a2 - 28a + 49

(iv) (3a - \(\frac{1}{2}\)) (3a - \(\frac{1}{2}\))
Answer:
(3a - \(\frac{1}{2}\)) (3a - \(\frac{1}{2}\)) = (3a - \(\frac{1}{2}\))2
= (3a)2 - 2(3a)(\(\frac{1}{2}\)) + (\(\frac{1}{2}\))2
[Using (a - b)2 = a2 - 2ab + b2]
= 9a2 - 3a + \(\frac{1}{4}\)

(v) (1.1 m - 0.4) (1.1m + 0.4)
Answer:
(1.1m.- 0.4) (1.1m + 0.4)
= (1.1m)2 - (0.4)2
[Using (a - b) (a + b) = a2 - b2]
= 1.21m2 - 0.16

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(vi) (a2 + b2) (- a2 + b2)
Answer:
(a2 + b2) (- a2 + b2) = (b2 + a2) (b2 - a2)
= (b2)2 - (a2)2
[Using (a + b) (a - b) = a2 - b2]
= b4 - a4

(vii) (6x - 7) (6x + 7)
Answer:
(6x - 7) (6x + 7) = (6x)2 - (7)2
= 36x2 - 49
[Using (a + b) (a - b) = a2 - b2]

(viii) (- a + c) (- a + c)
Answer:
(- a + c) (- a + c) = (- a + c)2
= (- a)2 + 2(- a) (c) + (c)2
[Using (a + b)2 = a2 - 2ab - b2]
= a2 - 2ab + b2
= a2 - 2ac + c2

(ix) \(\left(\frac{x}{2}+\frac{3 y}{4}\right)\left(\frac{x}{2}+\frac{3 y}{4}\right)\)
Answer:
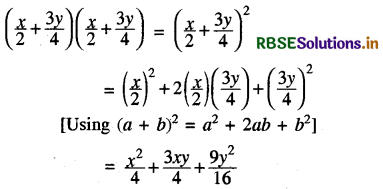
RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 1

(x) (7a - 9b) (7a - 9b)
Answer:
(7a - 9b) (7a - 9b) = (7a - 9b)2
= (7a)2 - 2(7a) (9b) + (9b)2
[Using (a - b)2 = a2 - 2ab + b2]
= 49a2 - 126ab + 81b2

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

Question 2.
Use the identity (x + a) (x + b) = x2 + (a + b) x + ab to find the following products
(i) (x + 3) (x + 7)
Answer:
(x + 3) (x + 7) = x2 + (3 + 7)x + 3 × 7
= x2 + 10x + 21

(ii) (4x + 5) (4x + 1)
Answer:
(4x + 5) (4x + 1) = (4x)2 + (5 + 1)(4x) + 5 × 1
= 16x2 + 24x + 5

(iii) (4x - 5) (4x - 1)
Answer:
(4x - 5) (4x - 1)= [4x + (-5)] [4x + (- 1)]
= (4x)2 + (- 5 - 1) (4x) + (- 5) (- 1)
= 16x2 - 24x + 5

(iv)(4x + 5) (4x - 1)
Answer:
(4x + 5) (4x - 1) = (4x + 5) [4x + (- 1)]
= (4x)2 + [5 + (- 1)] (4x) + (5) (-1)
= 16x2 + 16x - 5

(v) (2x + 5y) (2x + 3y)
Answer:
(2x + 5y) (2r + 3y) = (2x)2 + (5y + 3y)(2x) + (5y) (3y)
= 4x2 + 16xy + 15y2

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(vi) (2a2 + 9) (2a2 + 5)
Answer:
(2a2 + 9) (2a2 + 5)
= (2a2)2 + (9 + 5) (2a2) + (9) (5)
= 4a4 + 28a2 + 45

(vii) (xyz - 4) (xyz - 2)
Answer:
(xyz - 4) (xyz - 2)
= (xyz)2 + (- 4 - 2) (xyz) + (-4) (-2)
= x2y2z2 - 6xyz + 8

Question 3.
Find the following squares by using the identities—
(i) (b - 7)2
Answer:
(b - 7)2 = b2 - 2(b) (7) + (7)2
= b2 - 14b + 49

(ii) (xy + 3z)2
Answer:
(xy + 3z)2 = (xy)2 + 2(xy) (3z) + (3z)2
= x2y2 + 6xyz + 9z2

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(iii) (6x2 - 5y)2
Answer:
(6x2 - 5y)2 = (6x2)2 - 2(6x2) (5y) + (5y)2
= 36x4 - 60x2y + 25y2

(iv) \((\frac{2}{3}m + \frac{3}{2}n)\)
Answer:
(\(\frac{2}{3}\)m + \(\frac{3}{2}\)n)2 = (\(\frac{2}{3}\)m)2 + 2(\(\frac{2}{3}\)m)(\(\frac{3}{2}\)n) + (\(\frac{3}{2}\)n)2
= \(\frac{4}{9}\)m2 + 2mn + \(\frac{9}{4}\)n2

(v) (0.4p - 0.5q)2
Answer:
(0.4p - 0.5q)2
= (0.4p)2 - 2(0.4p) (0.5q) + (0.5q)2
= 0.16p2 - 0.4pq + 0.25q2

(vi) (2xy + 5y)2
Answer:
(2xy + 5y)2 = (2xy)2 + 2(2xy) (5y) + (5y)2
= 4x2y2 + 20xy2 + 25y2

Question 4.
Simplify
(i) (a2 - b2)2
(ii) (2x + 5)2 - (2x - 5)2
(iii) (7m - 8n)2 + (7m + 8n)2
(iv) (4m + 5n)2 + (5m + 4n)2
(v) (2.5p - 1.5q)2 - (1.5p - 2.5q)2
(vi) (ab + bc)2 - 2ab2c
(vii) (m2 - n2m)2 + 2m3n2
Answer:
(i) (a2 - b2)2 = (a2)2 - 2(a2) (b2) + (b2)2
[Using (a - b)2 = a2 - 2ab + b2]
= a4 - 2a2b2 + b4

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(ii) (2x + 5)2 - (2x - 5)2
= (4x2 + 20x + 25) - (4x2 - 20x + 25)
= 4x2 + 20x + 25 - 4x2 + 20x - 25
= 40x

(iii) (7m - 8n)2 + (7m + 8n)2
= (49m2 - 112mn + 64n2) + (49m2 + 112mn + 64n2)
= 49m2 - 112mn + 64n2 + 49m2 + 112m + 64n2
= 98m2 + 128n2

(iv) (4m + 5n)2 + (5m + 4n)2
= (16m2 + 40mn + 25n2) + (25 m2 + 40mn + 16n2)
= (16 + 25 )m2 + (40 + 40)mn + (25 + 16)n2
= 41m2 + 80mn + 41 n2

(v) (2.5p - 1.5q)2 - (1.5p - 2.5q)2
= (6.25p2 - 7.5pq + 2.25q2) - (2.25p2 - 7.5pq + 6.25 q2)
= (6.25 - 2.25)p2 + (- 7.5 + 7.5) pq + (2.25 - 6.25)q2
= 4p2 + (0)pq - 4q2
= 4p2 - 4q2

(vi) (ab + bc)2 - 2ab2c
= (ab)2 + 2 (ab) (bc) + (bc)2 - 2ab2c
= a2b2 + 2ab2c + b2c2 - 2ab2c
= a2b2 + b2c2

(vii) (m2 - n2m)2 + 2m3n2
= m4 - 2(m2)(n2m) + (n2m)2 + 2m3n2
= m4 - 2m3n2 + n4m2 + 2m3n2 = m4 + n4m2

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

Question 5.
Show that
(i) (3x + 7)2 - 84x = (3x - 7)2
(ii) (9p - 5q)2 + 180pq = (9p + 5q)2
(iii) (\(\frac{4}{3}\)m - \(\frac{3}{4}\)n)2 + 2mn = \(\frac{16}{9}\)m2 + \(\frac{9}{16}\)n2
(iv) (4pq + 3q)2 - (4pq - 3q)2 = 48pq2
(v) (a - b) (a +b) + (b - c) (b +c) + (c - a) (c + a) = 0
Answer:
(i) LHS = (3x + 7)2 - 84x
= (9x2 + 42x + 49) - 84x
= 9x2 - 42x + 49
= (3x)2 - 2(3x)(7) + (7)2
= (3x - 7)2 = RHS

(ii) LHS = (9p - 5q)2 + 180pq
= 81p2 - 90pq + 25q2 + 180pq
= 81 p2 + 90 pq + 25 q2
= (9p)2 + 2(9p)(5q) + (5 q)2
= (9p + 5 q)2
= RHS

(iii)
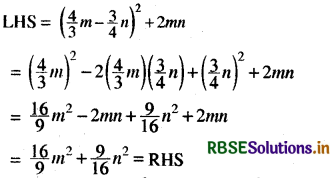
RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 2

(iv) LHS = (4pq + 3q)2 - (4pq - 3q)2
= (16p2q2 + 24pq2 + 9q2) - (16p2q2 - 24pq2 + 9q2)
= 48pq2 = RHS

(v ) LHS = (a - b) (a + b) + (b - c) (b + c) + (c - a) (c + a)
= a2 - b2 + b2 - c2 + c2 - a2
= (a2 - a2) + (-b2 + b2) + (- c2 + c2)
= 0 + 0 + 0 = 0 = RHS

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

Question 6.
Using identities, evaluate :
(i) 712
Answer:
We have
712 = (70 + 1)2
= (70)2 + 2 × 70 × 1 + (1)2
[Using (a + b)2 = a2 + 2ab + b2]
= 4900 + 140 + 1 = 5041

(ii) 992
Answer:
992 = (100 - 1)2
= (100)2 - 2 × 100 × 1 + (1)2
[Using (a - b)2 = a2 - 2ab + b2]
= 10000 - 200 + 1 = 9801

(iii) 1022
Answer:
1022 = (100 + 2)2
= (100)2 + 2 × 100 × 2 + (2)2
[Using (a + b)2 = a2 + 2ab + b2]
= 10000 + 400 + 4
= 10404

(iv) 9982
Answer:
9982 = (1000 - 2)2
= (10002) - 2 × 1000 × 2 + (2)2
[Using (a - b)2 = a2 - 2ab + b2]
= 1000000 - 4000 + 4
= 996004

(v) 5.22
Answer:
5.22 = (5 + 0.2)2
= (5)2 + 2 × 5 × 0.2 + (0.2)2
[using (a + b)2 = a2 + 2ab + b2]
= 25 + 2 + 0.04 = 27.04

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(vi) 297 × 303
Answer:
297 × 303 = (300 - 3) × (300 + 3)
= (300)2 - (3)2
[Using (a - b) (a + b) = a2 - b2]
= 90000 - 9 = 89991

(vii) 78 × 82
Answer:
78 × 82 = (80 - 2) × (80 + 2)
= (80)2 - (2)2
[Using (a - b) (a + b) = a2b2]
= 6400 - 4 = 6396

(viii) 8.92
Answer:
8.92 = (9 - 0.1)2
= (9)2 - 2(9)(0.1) + (0.1)2
[Using (a - b)2 = a2 - 2ab + b2]
= 81 - 1.8 + 0.01=79.21

(ix) 1.05 × 9.5
Answer:
1.05 × 9.5 = (1 + .05) 9.5
= 1 × 9.5 + 0.05 × 9.5
= 9.5 + 0.475 = 9.975

Question 7.
Using a2 - b2 = (a + b) (a - b), find
(i) 512 - 492
Answer:
512 - 492 = (51 + 49) (51 - 49)
= (100) (2) = 200

(ii) (1.02)2 - (0.98)2
Answer:
(1.02)2 - (0.98)2
= (1.02 + 0.98) (1.02 - 0.98) = (2) (0.04) = 0.08

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(iii) 1532 - 1472
Answer:
(153)2 - (147)2
= (153 + 147) (153 - 147)
= (300) (6) = 1800

(iv) 12.12 - 1.92
Answer:
12.12 - 7.92
= (12.1 + 7.9) (12.1 - 7.9)
= (20) (4.2) = 84

Question 8.
Using (x + a) (x + b) = x2 + (a + b) x + ab find
(i) 103 × 104
Answer:
103 × 104 = (100 + 3) (100 + 4)
= (100)2 + (3 + 4) (100) + (3) (4)
= 10000 + 700 + 12
= 10712

(ii) 5.1 × 5.2
Answer:
5.1 × 5.2= (5 + .1) (5 + .2)
= (5)2 + (.1 + .2 )(5) + (.1)(.2)
= 25 + 1.5 + 0.02
= 26.52

(iii) 103 × 98
Answer:
103 × 98= (100 + 3) [100 + (- 2)|
= (100)2 + [3 + (-2)] (100) + (3)(- 2)
= 10000 + 100 - 6
= 10094

RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

(iv) 9.7 × 9.8
Answer:
9.7 × 9.8 = (9 + .7)(9 + .8)
= (9)2 + (.7 + .8)(9) + (.7)(.8)
= 81 + 13.5 + 0.56
= 95.06  

Bhagya
Last Updated on May 19, 2022, 2:57 p.m.
Published May 19, 2022