RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.3

Question 1.
Carry out the multiplication of the expressions in each of the following pairs : '
(i) 4p, q + r
Answer:
4p × (q + r) = 4p × q + 4p × r
= 4pq + 4pr

(ii) ab, a - b
Answer:
ab × (a - b) = ab × a - ab × b
= a²b - ab²

(iii) a + b, 7a²b²
Answer:
(a + b) × 7a²b² = a × 7a²b² + b × 7a²b²
= 7a³b² + 7a²b³

(iv) a² - 9, 4a
Answer:
(a² - 9) × 4a = a² × 4a - 9 × 4a
= 4a³ - 36a

(v) pq + qr + rp, 0
Answer:
(pq + qr + rp) × 0 = 0

Question 2.
Complete the table.

Answer:
Completed table is as under:

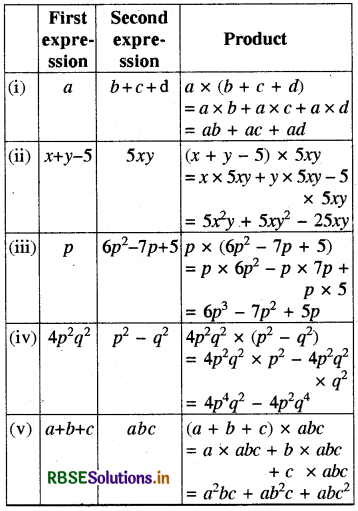
Question 3.
Find the product,
(i) (a²) × (2a²²) × (4a²⁶)
(ii) (\(\frac{2}{3}\)xy) × (\(\frac{-9}{10}\)x²y²)
(iii) (-\(\frac{10}{3}\)pq³) × (\(\frac{6}{5}\)P³q)
(iv) x × x² × x³ × x⁴
Answer:
(i) (a²) × (2a²²) × (4a²⁶)
= (1 × 2 × 4) × (a² × a²² × a²⁶)
= 8a^{2 + 22 + 26}
= 8a⁵⁰

(ii) (\(\frac{2}{3}\)xy) × (\(\frac{-9}{10}\)x²y²)
= \(\left(\frac{2}{3} \times \frac{-9}{10}\right)\) × (x × x² × y × y²)
= -\(\frac{3}{5}\) × x¹⁺² × y¹⁺²
= -\(\frac{3}{5}\) × x³ × y³

(iii) \(\left(-\frac{10}{3} p q^{3}\right) \times\left(\frac{6}{5} p^{3} q\right)\)
= \(\left(-\frac{10}{3} \times \frac{6}{5}\right)\) × (p × p³ × q³ × q)
= - 4 × p^{1 + 3} × q^{3 + 1}
= - 4p⁴q⁴

(iv) x × x² × x³ × x⁴
= x^{1 + 2 + 3 + 4}
= x¹⁰

Question 4.
(a) Simplify 3x (4x - 5) + 3 and find its values for (i) x = 3 (ii) x = \(\frac{1}{2}\).
(b) Simplify a (a² + a + 1) + 5 and find its value for (i) a = 0, (ii) a = 1 (iii) a = - 1.
Answer:
(a) We have
3x (4x - 5) + 3 = 3x × 4x - 3x × 5 + 3
= 12x² - 15x + 3

(i) If x = 3, then
3x(4x - 5) + 3 = 3 × 3(4 × 3 - 5) + 3
= 9(12 - 5) + 3 = 9 × 7 + 3
= 63 + 3
= 66

(ii) If x = \(\frac{1}{2}\), then
3x(4x - 5) + 3 = 3 × \(\frac{1}{2}\)(4 × \(\frac{1}{2}\) - 5) + 3
= \(\frac{3}{2}\)(2 - 5) + 3 = \(\frac{3}{2}\) × - 3 + 3
= \(\frac{-9+6}{2}\) = \(\frac{-3}{2}\)

(b) a(a² + a + 1) + 5 = a³ + a² + a + 5
(i) If a = 0, then
a(a² + a + 1) + 5 = 0 (0 + 0 + 1) + 5 = 0 + 5 = 5

(ii) If a = 1, then
a(a² + a + 1) + 5 = 1 (1 + 1 + 1) + 5 = 3 + 5 = 8

(iii) If a = - 1, then
a(a² + a + 1) + 5 = - 1(1 - 1 + 1) + 5 = - 1 + 5 = 4

Question 5.
(a) Add :
p (p - q), q (q - r) and r (r - p)
Answer:
p (p - q) + q (q - r) + r (r - p)
= p × p - p × q + q × q - q × r + r × r - r × p
= p² - pq + q² - qr + r² - pr
= p² + q² + r² - pq - qr - pr

(b) Add : 2x (z - x - y) and 2y (z - y - x)
Answer:
2x (z - x - y) + 2y (z - y - x)
= 2xz - 2x² - 2xy + 2yz - 2y² - 2xy
= - 2x² - 2y² + 2xz + 2yz + (- 2 - 2) xy
= - 2x² - 2y² + 2xz + 2yz - 4xy

(c) Subtract : 3l (l - 4m + 5n) from 4l (10n - 3m + 2l)
Answer:
4l (10n - 3m + 2l) - 3l (l - 4m + 5n)
= 40ln - 12lm + 8l² - 3l² + 12lm - 15ln
= (40 - 15)ln + (- 12 + 12)lm + (8 - 3)l²
= 25ln + 5l²

(d) Subtract: 3a (a + b + c) - 2b (a - b + c) from 4c (- a + b + c)
Answer:
4c (- d + b + c) - [3a (a + b + c) - 2b (a - b + c)]
= 4c (- a + b + c) - 3d(d + b + c) + 2b(a - b + c)
= - 4ca + 4bc + 4c² - 3a² - 3ab - 3ca + 2 ab - 2 b² + 2 bc
= - 3a² - 2b² + 4c² + (- 3 + 2) db + (4 + 2)bc + (- 4 - 3)ca
= - 3a² - 2b² + 4c² - ab + 6bc - 7ca