RBSE Solutions for Class 8 Maths Chapter 8 राशियों की तुलना Ex 8.3

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 8 राशियों की तुलना Ex 8.3 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 8 राशियों की तुलना Ex 8.3

Class 8 Maths Ex 8.3 Solutions In Hindi प्रश्न 1.
निम्नलिखित के लिए कुल राशि एवं चक्रवृद्धि ब्याज ज्ञात कीजिए
(a) 10,800 रुपए पर 3 वर्ष के लिए 121% वार्षिक दर से वार्षिक रूप से संयोजित करने पर।
हल:
दिया है, P = 10,800 रुपए 
R = 12\(\frac{1}{2}\)% वार्षिक = \(\left(\frac{25}{2}\right)\) प्रति वर्ष और n = 3 वर्ष
∴ 3 वर्ष बाद मिश्रधन = [10800 × \(\left(1+\frac{25}{2 \times 100}\right)^{3}\)] रुपए
= (108000 × \(\frac{9}{8} \times \frac{9}{8} \times \frac{9}{8}\)) रुपए
= 15377.34 रुपए 

चक्रवृद्धि ब्याज = (15377.34 - 10800) रुपए
= 4577.34 रुपए 

(b) 18,000 रुपए पर 21 वर्ष के लिए 10% वार्षिक दर से वार्षिक रूप से संयोजित करने पर।
हल:
यहाँ P= 18000 रुपए, R= 10% वार्षिक और T= 2\(\frac{1}{2}\) वर्ष
2\(\frac{1}{2}\) वर्ष के बाद मिश्रधन
= [18000 × \(\left(1+\frac{10}{100}\right)^{2} \times\left(1+\frac{\frac{1}{2} \times 10}{100}\right)\)] रुपए
= (18000 × \(\frac{110}{100} \times \frac{110}{100} \times \frac{105}{100}\)) रुपए
= 22869 रुपए 

∴ चक्रवृद्धि ब्याज = (22869 - 18000) रुपए
= 4869 रुपए 

(c) 62,500 रुपए पर 11 वर्ष के लिए 8% वार्षिक दर से अर्धवार्षिक रूप से संयोजित करने पर।
हल:
यहाँ मूलधन = 62500 रुपए दर = 8% वार्षिक = 4% छमाही समय = 1\(\frac{1}{2}\), वर्ष = 3 छमाही
∴ मिश्रधन = [62500 × \(\left(1+\frac{4}{100}\right)^{3}\)] रुपए
= (62500 × \(\frac{104}{100} \times \frac{104}{100} \times \frac{104}{100}\)) रुपए
= 70304 रुपए 

चक्रवृद्धि ब्याज = (70304 - 62500) रुपए
= 7804 रुपए 

(d) 8,000 रुपए पर 1 वर्ष के लिए 9% वार्षिक दर से अर्धवार्षिक रूप से संयोजित करने पर।
हल:
यहाँ मूलधन = 8000 रुपए, समय = 1 वर्ष = 2 छमाही, दर = 9% वार्षिक = \(\left(\frac{9}{2}\right)\)% छमाही 
∴ मिश्रधन = [8000 × \(\left(1+\frac{9}{2 \times 100}\right)^{2}\)] रुपए
= (8000 × \(\frac{209}{200} \times \frac{209}{200}\)) रुपए
- = 8736.20 रुपए
∴ चक्रवृद्धि ब्याज = (8736.20 - 8000) रुपए
= 736.20 रुपए

(e) 10,000 रुपए पर 1 वर्ष के लिए 8% वार्षिक दर से अर्धवार्षिक रूप से संयोजित करने पर।
हल:
दिया है, P = 10000 रुपए, R = 8% वार्षिक = 4% छमाही और i = 1 वर्ष = 2 छमाही
1 वर्ष के बाद मिश्रधन = 10000 × \(\left(1+\frac{4}{100}\right)^{2}\) रुपए
= (10000 × \(\frac{104}{100} \times \frac{104}{100}\)) रुपए
= (10000 × \(\frac{26}{25} \times \frac{26}{25}\)) रुपए
= 10816 रुपए 

चक्रवृद्धि ब्याज = (10816 - 10000) रुपए
= 816 रुपए 

Class 8 Maths 8.3 In Hindi प्रश्न 2.
कमला ने एक स्कूटर खरीदने के लिए किसी बैंक से 26400 रुपए 15% वार्षिक दर से उधार लिए जबकि ब्याज वार्षिक संयोजित होना है। 2 वर्ष और 4 महीने के अन्त में उधार चुकता करने के लिए उसे कितनी राशि का भुगतान करना पड़ेगा?
हल:
यहाँ, P = 26400 रुपए, R = 15% वार्षिक और n = 2 वर्ष 4 महीने = 2\(\frac{1}{3}\) वर्ष
2\(\frac{1}{3}\) वर्ष बाद मिश्रधन
= [26400 × \(\left(1+\frac{15}{100}\right)^{2} \times\left(1+\frac{\frac{1}{3} \times 15}{100}\right)\)]
= (26400 × \(\frac{115}{100} \times \frac{115}{100} \times \frac{105}{100}\)) रुपए 
= (26400 × \(\frac{23}{20} \times \frac{23}{20} \times \frac{21}{20}\)) रुपए
= 36659.70 रुपए
अतः कमला को 36659.70 रुपए बैंक को अदा करने पड़ेंगे। 

Class 8 Math 8.3 Solution In Hindi प्रश्न 3.
फैबिना ने 12,500 रुपए 3 वर्ष के लिए 12% वार्षिक दर से साधारण ब्याज पर उधार लिए और राधा ने उतनी ही राशि उतने ही समय के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज पर उधार ली जबकि ब्याज वार्षिक रूप से संयोजित होना है। किसे अधिक ब्याज का भुगतान करना है और कितना अधिक करना है?
हल:
फैबिना के लिए P = 12500 रुपए, R = 12% वार्षिक और T = 3 वर्ष, तो 
साधारण ब्याज = \(\frac{P \times R \times T}{100}\)
= \(\left(\frac{12500 \times 12 \times 3}{100}\right)\) रुपए
= 4500 रुपए

राधा के लिए P = 12500 रुपए, R = 10% वार्षिक और n = 3 वर्ष, तो 
मिश्रधन = 12500 × \(\left(1+\frac{10}{100}\right)^{3}\) रुपए
= (12500 × \(\frac{110}{100} \times \frac{110}{100} \times \frac{110}{100}\)) रुपए
= 16637.50 रुपए 
∴ चक्रवृद्धि ब्याज = (16637.50 - 12500) रुपए
= 4137.50 रुपए
दोनों ब्याजों में अन्तर = (4500 - 4137.50) रुपए
= 362.50 रुपए
अतः, फैबिना 362.50 रुपए अधिक अदा करेगी।

8.3 Class 8 In Hindi प्रश्न 4.
मैंने जमशेद से 12,000 रुपए 2 वर्ष के लिए 6% वार्षिक दर से साधारण ब्याज पर उधार लिए। यदि मैंने यह राशि 6% वार्षिक दर से चक्रवृद्धि ब्याज पर उधार ली हुई होती तो मुझे कितनी अतिरिक्त राशि का भुगतान करना पड़ता?
हल:
यहाँ, P = 12000 रुपए, R = 6% वार्षिक और T = 2 वर्ष
साधारण ब्याज = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\left(\frac{12000 \times 6 \times 2}{100}\right)\) रुपए
= 1440 रुपए

चक्रवृद्धि ब्याज के लिए
मिश्रधन = [12000 × \(\left(1+\frac{6}{100}\right)^{2}\)] रुपए
= (12000 + \(\frac{106}{100} \times \frac{106}{100}\)) रुपए
= 13483.20 रुपए 
∴ चक्रवृद्धि ब्याज = (13483.20 - 12000) रुपए
= 1483.20 रुपए
अतः मुझे (1483.20 - 1440) रुपए = 43.20 रुपए अतिरिक्त राशि का भुगतान करना पड़ता। 

Class 8 Maths Chapter 8 Exercise 8.3 In Hindi Medium प्रश्न 5.
वासुदेवन ने 12% वार्षिक दर पर 60,000 रुपए का निवेश किया। यदि ब्याज अर्धवार्षिक संयोजित होता है तो ज्ञात कीजिए कि वह
(i) 6 महीने के अन्त में
(ii) एक वर्ष के अन्त में, कुल कितनी राशि प्राप्त करेगा?
हल:
यहाँ, मूलधन = 60000 रुपए, दर = 12% वार्षिक = 6% छमाही 
(i) समय = 6 महीने = 1 छमाही 
∴ 6 महीने बाद मिश्रधन
= [60000 × \(\left(1+\frac{6}{100}\right)^{1}\)] रुपए
= (60000 × \(\frac{106}{100}\)) रुपए
= 63600 रुपए उत्तर

(ii) समय = 1 वर्ष = 2 छमाही ।
∴ 1 वर्ष बाद मिश्रधन = 60000 × \(\left(1+\frac{6}{100}\right)^{2}\) रुपए
= (60000 × \(\frac{106}{100} \times \frac{106}{100}\)) रुपए
= 67416 रुपए

Class 8th Maths Chapter 8 Exercise 8.3 In Hindi प्रश्न 6.
आरिफ ने एक बैंक से 80,000 रुपए का कर्ज लिया। यदि ब्याज की दर 10% वार्षिक है तो 11 वर्ष पश्चात् उसके द्वारा भुगतान की जाने वाली राशियों में अन्तर ज्ञात कीजिए। यदि ब्याज
(i) वार्षिक संयोजित होता है
(ii) अर्धवार्षिक संयोजित होता है।
हल:
यहाँ, P = 80000 रुपए, दर = 10% वार्षिक = 5% प्रति छमाही, समय = 1\(\frac{1}{2}\) वर्ष = 3 छमाही
(i) जब चक्रवृद्धि ब्याज वार्षिक संयोजित होता है 1\(\frac{1}{2}\) वर्ष बाद मिश्रधन

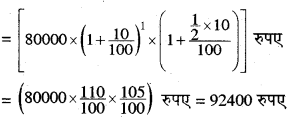
(ii) जब चक्रवृद्धि ब्याज अर्धवार्षिक संयोजित होता
1\(\frac{1}{2}\) वर्ष बाद 
मिश्रधन = [80000 + \(\left(1+\frac{5}{100}\right)^{3}\)] रुपए
= (80000 × \(\frac{105}{100} \times \frac{105}{100} \times \frac{105}{100}\)) रु.
= 92610 रुपए 

∴ मिश्रधनों का अन्तर = (92610 - 92400) रुपए
= 210 रुपए

Class 8 Math Chapter 8.3 In Hindi प्रश्न 7.
मारिया ने किसी व्यापार में 8000 रुपए का निवेश किया। उसे 5% वार्षिक दर से चक्रवृद्धि ब्याज का भुगतान किया जाएगा। यदि ब्याज वार्षिक रूप से संयोजित होता है तो
(i) दो वर्ष के अन्त में उसके नाम से जमा की गई राशि ज्ञात कीजिए।
(ii) तीसरे वर्ष का ब्याज ज्ञात कीजिए।
हल:
(i) यहाँ, P = 8000 रुपए, R = 5% वार्षिक और n = 2 वर्ष
∴ 2 वर्ष बाद मिश्रधन = P\(\left(1+\frac{\mathrm{R}}{100}\right)^{n}\)
= [8000 × \(\left(1+\frac{5}{100}\right)^{2}\)] रुपए
= (8000 × \(\frac{105}{100} \times \frac{105}{100}\)) रुपए
= 8820 रुपए 

(ii) तीसरे वर्ष के लिए मूलधन = 8820 रुपए
∴ तीसरे वर्ष का ब्याज = \(\left(\frac{8820 \times 5 \times 1}{100}\right)\) रुपए
= 441 रुपए 

Class 8 Maths Chapter 8.3 In Hindi प्रश्न 8.
10,000 रुपए पर 1\(\frac{1}{2}\) वर्ष के लिए 10% वार्षिक दर से चक्रवृद्धि ब्याज और कुल राशि ज्ञात कीजिए जबकि ब्याज अर्धवार्षिक संयोजित होना है। क्या यह ब्याज उस ब्याज से अधिक होगा जो उसे वार्षिक रूप से संयोजित करने पर प्राप्त होगा?
हल:
यहाँ, मूलधन = 10000 रुपए, समय = 1\(\frac{1}{2}\) वर्ष = 3 छमाही, दर = 10% वार्षिक = 5% प्रति छमाही
∴ 1\(\frac{1}{2}\) वर्ष बाद मिश्रधन
= [10000 × \(\left(1+\frac{5}{100}\right)^{3}\)] रुपए
= (10000 × \(\frac{105}{100} \times \frac{105}{100} \times \frac{105}{100}\)) रुपए
= (10000 × \(\frac{21}{20} \times \frac{21}{20} \times \frac{21}{20}\)) रुपए
= 11576.25 रुपए
और चक्रवृद्धि ब्याज = (11576.25 - 10000) रुपए
= 1576.25 रुपए
हाँ, यह ब्याज वार्षिक संयोजित होने वाले ब्याज से अधिक : है। यह अग्र प्रकार स्पष्ट है-
वार्षिक रूप से संयोजित करने पर प्राप्त मिश्रधन
= 10000 × \(\left(1+\frac{10}{100}\right) \times\left(1+\frac{\frac{1}{2} \times 10}{100}\right)\)
= 10000 × \(\frac{110}{100} \times \frac{105}{100}\)
= 11550 रुपए

तथा इस प्रकार प्राप्त चक्रवृद्धि ब्याज
= 11550 रु. - 10000 रु. = 1550 रु. 
अतः अर्धवार्षिक रूप से संयोजित ब्याज वार्षिक संयोजित ब्याज से अधिक होगा। 

Class 8 Maths 8.3 Hindi Medium प्रश्न 9.
यदि राम 4096 रुपए 18 महीने के लिए 12\(\frac{1}{2}\)% वार्षिक दर पर उधार देता है और ब्याज अर्धवार्षिक संयोजित होता है तो ज्ञात कीजिए कि राम कल कितनी राशि प्राप्त करेगा?
हल:
यहाँ, मूलधन = 4096 रुपए, समय = 18 महीने 1 = 3 छमाही, दर = 12\(\frac{1}{2}\)%
वार्षिक = \(\left(\frac{25}{2} \times \frac{1}{2}\right)% = \frac{25}{4}\) प्रति छमाही 

मिश्रधन = [ 4096 × \(\left(1+\frac{25}{4 \times 100}\right)^{3}\)] रुपए
= (4096 × \(\frac{425}{400} \times \frac{425}{400} \times \frac{425}{400}\)) रुपए
= (4096 × \(\frac{17}{16} \times \frac{17}{16} \times \frac{17}{16}\)) रुपए
= 4913 रुपए

8th Class Math 8.3 In Hindi प्रश्न 10.
5% वार्षिक दर से बढ़ते हुए वर्ष 2003 के अन्त में एक स्थान की जनसंख्या 54000 हो गई। निम्नलिखित को ज्ञात कीजिए
(i) वर्ष 2001 में जनसंख्या
हल:
माना 2001 में जनसंख्या P थी, 
अतः वर्तमान जनसंख्या = P × \(\left(1+\frac{5}{100}\right)^{2}\)
या 54000 = P × \(\frac{105}{100} \times \frac{105}{100}\)
P = \(\frac{54000 \times 100 \times 100}{105 \times 105}\)
= 48979.59
अतः. 2001 में जनसंख्या 48980 (लगभग) 

(ii) वर्ष 2005 में कितनी जनसंख्या होगी?
हल:
2003 में जनसंख्या (P) = 54000
∴ 2 वर्ष बाद अर्थात् 2005 में जनसंख्या
= P\(\left(1+\frac{\mathrm{R}}{100}\right)^{n}\)
= 54000 × \(\left(1+\frac{5}{100}\right)^{2}\)
= 54000 × \(\frac{105}{100} \times \frac{105}{100}\)
= 59535

Class 8 Maths Exercise 8.3 Solutions In Hindi प्रश्न 11.
एक प्रयोगशाला में, किसी निश्चित प्रयोग में बैक्टीरिया की संख्या 2.5% प्रति घण्टे की दर से बढ़ रही है। यदि प्रयोग के शुरू में बैक्टीरिया की संख्या 5,06,000 थी तो 2 घण्टे के अन्त में बैक्टीरिया की संख्या ज्ञात कीजिए।
हल:
दिया हैं, P = बैक्टीरिया की वास्तविक संख्या = 506000, वृद्धि दर,(R) = 2.5% प्रति घण्टा, समय = 2 घण्टे
∴ 2 घण्टे बाद बैक्टीरिया की संख्या
= 506000 × \(\left(1+\frac{2.5}{100}\right)^{2}\)
= 506000 × \(\frac{102.5}{100} \times \frac{102.5}{100}\)
= 531616.25
= 531616 (लगभग)

8th Class Math Exercise 8.3 In Hindi प्रश्न 12.
एक स्कूटर 42,000 रुपए में खरीदा गया। 8% वार्षिक दर से इसके मूल्य का अवमूल्यन हो गया। 1 वर्ष के बाद स्कूटर का मूल्य ज्ञात कीजिए।
हल:
दिया है, मूल्य (P) = 42000 रुपए - अवमूल्यन दर (R) = 8% वार्षिक 
∴ 1 वर्ष बाद मूल्य = P\(\left(1-\frac{R}{100}\right)\)
= [42000 × \(\left(1-\frac{8}{100}\right)\)] रुपए 
= (42000 × \(\frac{92}{100}\)) रुपए
= 38640 रुपए