RBSE Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 8 Comparing Quantities Ex 8.2

Question 1.
A man got a 10% increase in his salary. If his new salary is ₹ 1,54,000, find his original salary.
Answer:
10% increase in salary means If previous salary ₹ 100, increased salary = ₹ 110
If new salary is ₹ 110, original salary is ₹ 100
New salary is ₹ 1,54,000, original salary is = \(\frac{100}{110}\) × 1.54,000 = 1,40,000
Original salary = ₹ 1,40,000

Question 2.
On Sunday 845 people went to the Zoo. On Monday only 169 people went. What is the percent decrease in the people visiting the Zoo on Monday?
Answer:
On Sunday the number of people went to Zoo = 845
On Monday, the number of people went to Zoo = 169
Decrease in the people visiting the Zoo = (845 - 169) = 676
∴ Percentage decrease
= \(\left(\frac{\text { Decrease in people }}{\text { Original People }} \times 100\right)\)
= (\(\frac{676}{845}\) × 100)% = 80%

Question 3.
A shopkeeper buys 80 articles for ₹ 2,400 and sells them for a profit of 16%. Find the selling price of one article.
Answer:
C.P. of 80 articles = ₹ 2400
Profit = 16%
S.P. of 80 articles = \(\left(\frac{100+\text { Profit } \%}{100}\right)\) × C.P.
= ₹ (\(\frac{100+16}{100}\) × 2400)
= ₹ (116 × 24) = ₹ 2784
S.P. of one article = ?
= ₹ 34.80

Question 4.
The cost of an article was ₹ 15,500. ₹ 450 were spent on its repairs. If it is sold for a profit of 15%, find the selling price of the article.
Answer:
The cost price of the article is equal to the price at which it was bought plus the repair cost.
∴ C.P. of the given article = ₹ (15,500 + 450)
= ₹ 15,950
∵ Profit = 15%
∴ Profit = 15% of? 15,950
= ₹ (\(\frac{15}{100}\) × 15,950)
= ₹ 2392.50
∴ S.P. = C.P. + Profit
= ₹ (15,950 + 2392.50)
= ₹ 18,342.50

Question 5. 
A VCR and TV were bought for ₹ 8,000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss percent on the whole transaction.
Answer:
For VCR, we have
C.P. = ₹ 8000 and loss = 4%
S.P = \(\left(\frac{100-\operatorname{loss} \%}{100}\right)\) × C.P
= ₹ (\(\frac{100-4}{100}\) × 8000)
= ₹ (96 × 80) 
= ₹ 7680

For TV, we have
C.P. = ₹ 8000 and
profit = 89%
S.P = \(\left(\frac{100+\text { Profit } \%}{100}\right)\) × C.P
= (\(\frac{100+8}{100}\) × 8000)
= ₹ (108 x 80) = ₹ 8640 
Total S.P. = ₹ (7680 + 8640)
= ₹ 16,320

Total C.P. = ₹ (8000 + 8000)
= ₹ 16,000 S.P. > C.P.
So, there is profit.

∴ Total Profit = S.P. -C.P.
= ₹ (16,320 - 16,000) = ₹ 320
Hence, profit percent
= (\(\frac{\text { Profit }}{\text { C.P. }}\) × 100)%
= (\(\frac{320}{16,000}\) × 100)%
= 2%

Question 6.
During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair, of jeans marked at ₹ 1450 and two shirts marked at ₹ 850 each?
Answer:
For a pair of jeans, we have
M.P. = ₹ 1450, Discount = 10%
∴ Discount = 10% of ₹ 1450
= ₹ (\(\frac{10}{100}\) × 1450) = ₹ 145
∴ S.P. = ₹ (1450 - 145)
= ₹ 1305
For two shirts, we have
M.P. = ₹ (850 × 2)
= ₹ 1700

Discount = 10%
∴ Discount = 10% of 1700
= ₹(\(\frac{10}{100}\) × 1700)
= ₹ 170
S.P = ₹ (1700 - 170)
= ₹ 1530
Hence, the customer has to pay ₹ (1305 + 1530), i.e., ₹ 2835. 

Question 7.
A milkman sold two of his buffaloes for ₹ 20,000 each. On one he made a gain of 5% and on the other a loss of 10%. Find his overall gain or loss. (Hint: Find CP of each)
Answer:
For the first buffalo, we have
S.P. = ₹ 20,000 and gain = 5% 

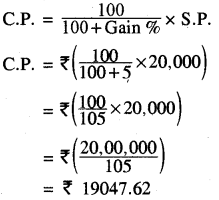
For the second buffalo, we have
S.P. = ₹ 20,000 and Loss = 10%

Total S.P. = ₹ (20,000 + 20,000)
= ₹ 40,000
∴ S.P. < C.P.

So, there is a loss.
∴ Total loss = C.P. - S.P.
= ₹ (41,269.84 - 40,000)
= ₹ 1269.84

Question 8.
The price of a TV is ₹ 13,000. The sales tax charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.
Answer:
Price of TV= ₹ 13,000
Sales tax charges = 12%
∴ Sales tax on TV = 12% of 13,000
= ₹ \(\frac{12}{100}\) × 13,000
= ₹ 1560
∴ Amount paid by Vinod for TV
= ₹ 13,000 + ₹ 1560 = ₹ 14,560

Question 9.
Arun bought a pair of skates at a sale where the discount given was 20%. If the amount he pays is ₹ 1,600, find the marked price.
Answer:
20% discount means for M.P. of ₹ 100, S.P.= ₹ (100 - 20) = ₹ 80
So, if S.P. = ₹ 80, M.P. is ₹ 100
If S.P. = ₹ 1600,

M.P. will be
= ₹ \(\frac{100}{80}\) × 1600 = 2000
M.P. of skates ₹ 2000

Question 10.
I purchased a hair-dryer for X 5,400 including 8% VAT, Find the price before VAT was added.
Answer:
Let the price of hair-dryer before VAT be ₹ x.
Then, VAT ₹ 8% on ₹ x = ₹ (\(\frac{8}{100}\) × x)
= ₹ \(\frac{8x}{100}\)

Thus, the sale price of hair-dryer
= ₹ (x + \(\frac{8x}{100}\))
= ₹ \(\frac{108 x}{100}\)

It is given that the sale price is ₹ 5400 
∴ \(\frac{108 x}{100}\) = 5400
⇒ x = \(\frac{5400 \times 100}{108}\)
or x = 5000
Hence, the price of hair-dryer before VAT was ₹ 5000. 

Question 11.
An article was purchased for 1239 including GST of 18%. Find the price of the article before GST was added?
Answer:
Price of article before GST was added = ₹ x
GST = 18% of x
= \(\frac{18}{100}\) × x
= \(\frac{18x}{100}\)

Price after GST added = x + \(\frac{18x}{100}\)
= \(\frac{100 x+18 x}{100}\)
= \(\frac{118 x}{100}\)
\(\frac{118 x}{100}\) = 1239
x = \(\frac{1239 \times 100}{118}\)
x = 1,050
The price before GST was added is ₹ 1,050.