RBSE Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 8 Comparing Quantities Ex 8.1

Question 1.
Find the ratio of the following.
(a) Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
Answer:
Speed of cycle which is 15 km/ hr to the speed of scooter which is 30 km/hr = 15 km : 30 km = \(\frac{1}{2}\) = 1:2

(b) 5 m to 10 km
Answer:
5 m to 10 km = 5 m : 10 km = 5 m : 10,000 m [∵ 1 km = 1000 m]
= 1 : 2000
[Dividing the first and second terms by their HCF = 5]

(c) 50 paise to ₹ 5
Answer:
50 paise to ₹ 5 [₹ 1 = 100 paise]
= 50 paise : ₹ 5 = 50 paise : 500 paise = 1 : 10
[Dividing the 1st and 2nd terms by their HCF = 50]

Question 2.
Convert the following ratios to percentages.
(a) 3 : 4
(b) 2 : 3
Answer:

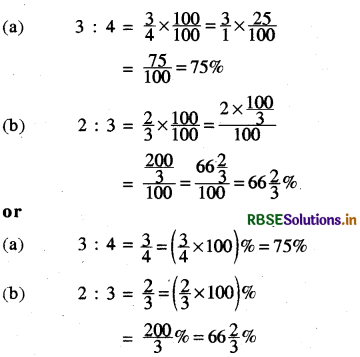
Question 3.
72% of 25 students are interested in mathematics. How many are not interested in mathematics?
Answer:
72% of 25 students are good in mathematics.
∴ (100 - 72)% i.e. 28% of 25 students are not good in mathematics.
Thus, their number = 28% of 25 = \(\frac{28}{100}\) × 25 = 7 students

Question 4.
A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?
Answer:
Let x games be played in all . Since 40% of die total games is given as 10
∴ 40% of x = 10
or \(\frac{40}{100}\) × x = 10
or x = \(\frac{10 \times 100}{40}\) = 25
Hence, the total games played were 25

Question 5.
If Chameli had ₹ 600 left after spending 75% of her money, how much did she have in the beginning?
Answer:
Let the total money she have in the beginning = ₹ x
Percentage of money spent by Chameli = 75%
∴ She is left with (100 - 75)% = 25%
But the money left = ? 600 (Given)
So, 25% of x= 600
or \(\frac{25}{100}\) × x =  600
or x = \(\frac{600 \times 100}{25}\) = ₹ 2400
Thus, she had ₹ 2400 in the beginning.

Question 6.
If 60% people in a city like cricket, 30% like football and the remaining like other games, then what per cent of the people like other games? If the total number of people are 50 lakh, find the exact number who like each type of game.
Answer:
∵ People who like cricket = 60%
People who like football = 30%
∴ People who like other games
= [100 - (60 + 30)]%
= (100 - 90)% = 10% 

Now, total number of people = 50 Lakh
∴ Cricket = 60% of 50
= \(\frac{60}{100}\) × 50 Lakh = 6 × 5 = 30 Lakh

Football = 30% of 50 = \(\frac{30}{100}\) × 50
= 15 Lakh
Other games = 10% of 50 lakh
= \(\frac{10}{100}\) × 50
= 5 Lakh