RBSE Solutions for Class 8 Maths Chapter 7 घन और घनमूल Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 7 घन और घनमूल Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 7 घन और घनमूल Intext Questions

(प्रयास कीजिए - पृष्ठ 119-I)

प्रश्न-निम्नलिखित संख्याओं में से प्रत्येक के घन के इकाई का अंक ज्ञात कीजिए
(i) 3331
(ii) 8888
(iii) 149
(iv) 1005
(v) 1024
(vi) 77
(vii) 5022
(viii) 53
हल:

(पृष्ठ 119-II)

प्रश्न 1.
निम्न प्रतिरूप का प्रयोग करते हुए, निम्नलिखित संख्याओं को विषम संख्याओं के योग के रूप में व्यक्त कीजिए
(a) 6³
(b) 8³
(c) 7³
हल:
प्रतिरूप
1 = 1 = 1³
3 + 5 = 8 = 2³
7 + 9 + 11 = 27 = 3³
13 + 15 + 17 + 19 = 64 = 4³
21 + 23 + 25 + 27 + 29 = 125 = 5³
उपरोक्त प्रतिरूप के प्रयोग से
(a) 6³ = 31 + 33 + 35 + 37 + 39 + 41 = 216
(b) 8³ = 57 + 59 + 61 + 63 + 65 + 67+ 69 + 71 = 512
(c) 7³ = 43 + 45 + 47 + 49 + 51 + 53 + 55 = 343

प्रश्न 2.
निम्नलिखित प्रतिरूप को देखिए
2³ - 1³ = 1 + 2 × 1 × 3
3³ - 2³ = 1 + 3 × 2 × 3
4³ - 3³ = 1 + 4 × 3 × 3
उपरोक्त प्रतिरूप का प्रयोग करते हुए निम्नलिखित के मान ज्ञात कीजिए
(i) 7³ - 6³
(ii) 12³ - 11³
(iii) 20³ - 19³
(iv) 51³ - 50³
हल:
दिए गए प्रतिरूप का प्रयोग करके
(i) 7³ - 6³ = 1 + 7 × 6 × 3 = 1 + 126 = 127
(ii) 12³ - 11³ = 1 + 12 × 11 × 3 = 1 + 396 = 397.
(iii) 20³ - 19³ = 1 + 20 × 19 × 3 = 1 + 1140 = 1141
(iv) 51³ - 50³ = 1 + 51 × 50 × 3 = 1 + 7650 = 7651

(प्रयास कीजिए - पृष्ठ 120)

प्रश्न-निम्नलिखित में से कौनसी संख्याएँ पूर्ण घन हैं?
(i) 400
(ii) 3375
(iii) 8000
(iv) 15625
(v) 9000
(vi) 6859
(vii) 2025
(viii) 10648
हल:
(i) 400 का अभाज्य गुणनखंड करने पर
400 = 2 × 2 × 2 × 2 × 5 × 5
समान गुणनखंडों को त्रिक बनाने पर 2 × 5 × 5 शेष बचते हैं।
∴ 400 एक पूर्ण घन नहीं है।

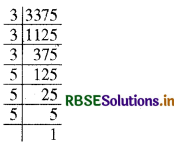
(ii) 3375 का अभाज्य गुणनखंड करने पर
3375 = 3 × 3 × 3 × 5 × 5 × 5
स्पष्ट है कि 3375 के समान गुणनखंडों के त्रिक बनाने के बाद कोई गुणनखंड नहीं बचता।
∴ 3375 पूर्ण घन है।

(iii) 8000 का अभाज्य गुणनखण्ड करने पर
8000 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5 स्पष्ट है कि 8000 के अभाज्य गुणनखंडों के त्रिक बनाने के बाद कोई गुणनखंड शेष नहीं बचता है।
∴ 8000 एक पूर्ण घन है।

(iv) 15625 का अभाज्य गुणनखंड करने पर
15625 = 5 × 5 × 5 × 5 × 5 × 5 स्पष्ट है कि 15625 के अभाज्य गुणनखंडों के त्रिक बनाने के बाद कोई भी गुणनखंड शेष नहीं बचता है।
∴ 15625 एक पूर्ण घन है।

(v) 9000 का अभाज्य गुणनखंड करने पर 9000 = 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5 अभाज्य गुणनखंडों के त्रिक बनाने पर 3 × 3 शेष बचते हैं।
∴ 9000 एक पूर्ण घन नहीं है।

(vi) 6859 का अभाज्य गुणनखंड करने पर
6859 = 19 × 19 × 19
स्पष्ट है कि 6859 के अभाज्य गुणनखंडों के त्रिक बनाने के बाद कोई गुणनखंड शेष नहीं बचता है।
∴ 6859 एक पूर्ण घन है।

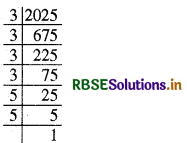
(vii) 2025 का अभाज्य गुणनखंड करने पर
2025 = 3 × 3 × 3 × 3 × 5 × 5.
अभाज्य गुणनखंडों के त्रिक बनाने पर
3 × 5 × 5 शेष बचते हैं।
∴ 2025 एक पूर्ण घन नहीं है।

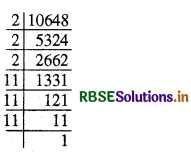
(viii) 10648 का अभाज्य गुणनखंड करने पर
10648 = 2 × 2 × 2 × 11 × 11 × 112
स्पष्ट है कि गुणनखंडों के त्रिक बनाने के बाद कोई गुणनखंड शेष नहीं बचता है।
∴ 10648 एक पूर्ण घन है।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 121)

प्रश्न-जाँच कीजिए कि निम्नलिखित में से कौनसी संख्याएँ पूर्ण घन हैं
(i) 2700
(ii) 16000
(iii) 64000
(iv) 900
(v) 125000
(vi) 36000
(vii) 21600
(viii) 10000
(ix) 27000000
(x) 1000
इन पूर्ण घनों में आप क्या प्रतिरूप देखते हैं?
हल:
(i) 2700 का अभाज्य गुणनखंड करने पर
2700 = 2 × 2 × 3 × 3 × 3 × 5 × 5
अभाज्य गुणनखंडों के त्रिक् बनाने पर चार गुणनखंड अर्थात् 2 × 2 × 5 × 5 शेष बचते हैं|
∴ 2700 एक पूर्ण घन नहीं है।

(ii) 16000 का अभाज्य गुणनखंड करने पर
16000 = 16 × 1000
= 2 × 2 × 2 × 2 × 10 × 10 × 10
= 2 × 2 × 2 × 2 × 2 × 5 × 2 × 5 × 2 × 5
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5
अब यदि हम अभाज्य गुणनखंडों के त्रिक बनाने का प्रयास करते हैं, तो एक गुणनखंड अर्थात् 2 शेष बचता है।
∴ 16000 एक पूर्ण घन नहीं है।

(iii) 64000 का अभाज्य गुणनखंड करने पर
64000 = 64 × 1000
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 2 × 5 × 2 × 5
= 2 × 2 × 2× 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5 स्पष्ट है कि 64000 के अभाज्य गुणनखंडों के त्रिक बनाने पर कोई भी गुणनखंड शेष नहीं बचता है।
∴ 64000 एक पूर्ण घन है।

(iv) 900 का अभाज्य गुणनखंड करने पर
900 = 9 × 100 = 3 × 3 × 10 × 10
= 3 × 3 × 2 × 5 × 2 × 5
= 2 × 2 × 3 × 3 × 5 × 5
अब यदि हम अभाज्य गुणनखंडों के त्रिक बनाने का प्रयास करते हैं, तो त्रिक नहीं बनता है।
∴ 900 एक पूर्ण घन नहीं है।

(v) 125000 का अभाज्य गुणनखंड करने पर
125000 = 125 × 1000
= 5 × 5 × 5 × 2 × 5 × 2 × 5 × 2 × 5
= 2 × 2 × 2 × 5 × 5 × 5 × 5 × 5 × 5
स्पष्ट है कि 125000 के अभाज्य गुणनखंडों के त्रिक बनाने पर कोई गुणनखंड शेष नहीं बचता है।
∴ 125000 एक पूर्ण घन है।

(vi) 36000 का अभाज्य गुणनखंड करने पर
36000 = 36 × 1000 = 6 × 6 × 10 × 10 × 10
= 2 × 3 × 2 × 3 × 2 × 5 × 2 × 5 × 2 × 5
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5
अब यदि हम अभाज्य गुणनखंडों के त्रिक बनाने का प्रयास करते हैं, तो चार गुणनखंड अर्थात् 2 × 2 × 3 × 3 शेष बचते हैं।
∴ 36000 पूर्ण घन नहीं है।

(vii) 21600 का अभाज्य गुणनखंड करने पर
21600 = 216 × 100 = 6 × 6 × 6 × 10 × 10
= 2 × 3 × 2 × 3 × 2 × 3 × 2 × 5 × 2 × 5
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5
अब यदि हम अभाज्य गुणनखंडों के त्रिक बनाने का प्रयास करते हैं, तो चार गुणनखंड अर्थात् 2 × 2 × 5 × 5 शेष बचते हैं।
∴ 21600 एक पूर्ण घन नहीं है।

(viii) 10000 का अभाज्य गुणनखंड करने पर
10000 = 10 × 10 × 10 × 10
= 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5
= 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5
अब यदि हम अभाज्य गुणनखंडों के त्रिक बनाने का प्रयास करते हैं, तो दो गुणनखंड अर्थात् 2 × 5 शेष बचते हैं।
∴ 10000 एक पूर्ण घन नहीं है।

(ix) 27000000 का अभाज्य गुणनखंड करने पर
27000000 = 27 × 10 × 10 × 10 × 10 × 10 × 10
= 3 × 3 × 3 × 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5
= 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5 × 5 × 5 × 5
स्पष्ट है 27000000 के अभाज्य गुणनखण्ड के पूर्ण त्रिक बन जाते हैं।
∴ 27000000 एक पूर्ण घन है।

(x) 1000 का अभाज्य गुणनखंड करने पर
1000 = 10 × 10 × 10 = 2 × 5 × 2 × 5 × 2 × 5
= 2 × 2 × 2 × 5 × 5 × 5.
स्पष्ट है कि 1000 के अभाज्य गुणनखंडों के पूर्ण त्रिक बन जाते हैं।
∴ 1000 एक. पूर्ण घन है।
उक्त में से पूर्ण घनों यथा 64000, 125000, 27000000
तथा 1000 में हमें यह प्रतिरूप देखने को मिलता है कि इनके अन्त में तीन अथवा छः शून्य हैं।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 123)

प्रश्न-बताइए कि सत्य है या असत्य-किसी पूर्णांक m के लिए m² < m³ होता है। क्यों?
हल:
m = 2, 3, 4, 5, आदि लेने पर हम देखते हैं।
जब m = 2:
m² = 2² = 2 × 2 = 4 और m³ = 2³ = 2 × 2 × 2 = 8
स्पष्ट है, 4 < 8 अर्थात् m² < m³

जब m = 3:
m² = 3² = 3 × 3 = 9 और m³ = 3³ = 3 × 3 × 3 = 27
स्पष्ट है, 9 < 27, अर्थात् m² < m³

जब m = 4:
m² = 4² = 4 × 4 = 16 और m³ = 4³ = 4 × 4 × 4 × 4 × 4 = 64
स्पष्ट है, 16 < 64, अर्थात् m² < m³

जब m = 5:
m² = 5² = 5 × 5 = 25 और m = 5³ = 5³ = 5 × 5 × 5 = 125
स्पष्ट है, 25 < 125, अर्थात् m² < m³
लेकिन जब m = 1,
m² = 1² = 1 × 1 = 1 और m³ = 1³ = 1 × 1 × 1 = 1
तो m² < m³
अतः, हम कह सकते हैं कि धन पूर्णांक (प्राकृत संख्या)
के लिए m > 1, m² > m³ सत्य है।
अब, माना m = - 1, -2, -3 आदि

जब m = -1:
m² = (-1)² = - 1 × - 1 = 1
और m³ = (-1)³ = - 1 × - 1 × - 1 = - 1
स्पष्ट है, 1 > - 1, अर्थात् m² > m³

जब m = - 2:
m² = (-2)² = - 2 × - 2 = 4 और
m³ = (-2)³ = - 2 × - 2 × - 2 = - 8
स्पष्ट है, 4 > - 8, अर्थात् m² > m³

जब m = -3:
m² = (-3)² = - 3 × - 3 = 9
और m³ = (-3)³ = - 3 × - 3 × - 3 = - 27
स्पष्ट है, 9 > - 27, अर्थात् m² > m³
लेकिन जब m = 0, तो m² = 0 और m³ = 0
∴ m² = m³
अतः हम कह सकते हैं कि किसी ऋण पूर्णांक m के लिए m² < m³ असत्य है।