RBSE Solutions for Class 8 Maths Chapter 7 Cube and Cube Roots Ex 7.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 7 Cube and Cube Roots Ex 7.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 7 Cube and Cube Roots Ex 7.2

Question 1.
Find the cube root of each of the following numbers by prime factorisation method.
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Answer:
(i) Resolving 64 into prime factors, we have
64 = 2 × 2 × 2 × 2 × 2 × 2
∴ \(\sqrt[3]{64}\) = (2 × 2) = 4

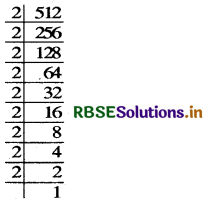
(ii) Resolving 512 into prime factors, we have
512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ \(\sqrt[3]{512}\) = (2 × 2 × 2) = 8

(iii) Resolving 10648 into prime factors, we have
10648 = 2 × 2 × 2 × 11 × 11 × 11
∴ \(\sqrt[3]{10648}\) = (2 × 11) = 22

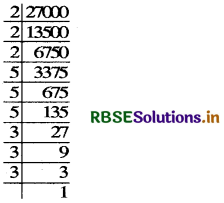
(iv) Resolving 27000 into prime factors, we have
27000 = 1000 × 27
= 10 × 10 × 10 × 3 × 3 × 3
= 2 × 5 × 2 × 5 × 2 × 5 × 3 × 3 × 3
= 2 × 2 × 2 × 5 × 5 × 5 × 3 × 3 × 3
∴ \(\sqrt[3]{27000}\) = 2 × 5 × 3 = 30

(v) Resolving 15625 into prime factors, we have
15625 = 5 × 5 × 5 × 5 × 5 × 5
∴ \(\sqrt[3]{15625}\) = 5 × 5 = 25

(vi) Resolving 13824 into prime factors, we get
13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
∴ \(\sqrt[3]{13824}\) = (2 × 2 × 2 × 3) = 24

(vii) Resolving 110592 into prime factors, we get
110592 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
∴ \(\sqrt[3]{110592}\) = (2 × 2 × 2 × 2 × 3)
= 48

(viii) Resolving 46656 into prime factors, we get
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
∴ \(\sqrt[3]{46656}\) = (2 × 2 × 3 × 3)
= 36

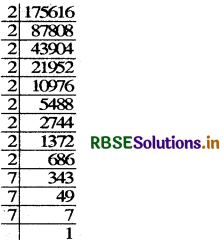
(ix) Resolving 175616 into prime factors, we get
175616 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7 × 7
∴ \(\sqrt[3]{175616}\) = (2×2×2×7) = 56

(x) Resolving 91125 into prime factors, we get
91125 = 3 × 3 × 3 × 3 × 3 × 3 × 5 × 5 × 5
∴ \(\sqrt[3]{91125}\) = (3 × 3 × 5)
= 45

Question 2.
State true or false.
(i) Cube of any odd number is even.
Answer:
False

(ii) A perfect cube does not end with two zeros.
Answer:
True

(iii) If square of a number ends with 5, then its cube ends with 25.
Answer:
False

(iv) There is no perfect cube which ends with 8.
Answer:
False

(v) The cube of a two digit number may be a three digit number.
Answer:
False

(vi) The cube of a two digit number may have seven or more digits.
Answer:
False

(vii) The cube of a single digit number may be a single digit number.
Answer:
True

Question 3.
You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Answer:
(a) 1331, yes; we can guess without prime factorisation. First of all we separate 1331 into two groups i.e. (one’s ten and hundreds place digit and remaining digit). So, 1331 → 331 and 1
∵ 331 ends in 1
∴ Unit’s digit of cube root = 1
1³ = 1 ⇒  \(\sqrt[3]{1}\) = 1
∴ Ten’s digit of cube root = 1
\(\sqrt[3]{1331}\) = 1

(b) We have 4913
4913 → 913 and 4
∵ 913 ends with 3
∴ Unit’s digit of cube root = 7
For ten’s digit of the cube root [∵ 73 = 343]
∵ 1³ = 1, 2³ = 8
and 1 < 4 < 8
∴ Ten’s digit of the cube root = 1
∴ \(\sqrt[3]{4913}\) = 17

(c) Let us separate 12167 in two groups :
12167 → 12 and 167
For unit’s digit
∵ 167 is ending in 7 and cube of a number ending in 3 ends in 7
∴ The unit’s digit of the cube root of 12167 = 3
For Ten’s digit
∵ 2³ = 8 and 3³ = 27
Thus 8 < 12 < 27
or 2³ < 12 < 3³
∴ The ten’s digit of the cube root will be 2.
Thus, \(\sqrt[3]{12167}\) = 23

(d) Let us separate 32768 in two groups : 32768 → 32 and 768
∵ 768 ends in 8.
∴ Unit’s digit in cube root of 32768 = 2
and 3³ = 27 , 4³ = 64
Thus 27 < 32 < 64
or 3³ < 32 < 4³
The ten’s digit of the cube root of 32768 = 3
Hence, \(\sqrt[3]{32768}\) = 32