RBSE Solutions for Class 8 Maths Chapter 6 वर्ग और वर्गमूल Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 6 वर्ग और वर्गमूल Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 6 वर्ग और वर्गमूल Intext Questions

(प्रयास कीजिए - पृष्ठ 96)

प्रश्न 1.
दी गई संख्याओं के बीच की पूर्ण वर्ग संख्याएँ ज्ञात कीजिए
(i) 30 और 40
हल:
5 × 5 = 25, 6 × 6 = 36 और 7 × 7 = 49 तीन पूर्ण वर्ग संख्याएँ हैं।
∴ 30 और 40 के बीच की पूर्ण संख्या 36 है।

(ii) 50 और 60
हल:
7 × 7 = 49 और 8 × 8 = 64 दो पूर्ण संख्याएँ हैं।
∴ 50 और 60 के बीच कोई भी पूर्ण वर्ग संख्या नहीं है।

(प्रयास कीजिए - पृष्ठ 97-I)

प्रश्न 1.
क्या हम कह सकते हैं कि निम्न संख्याएँ पूर्ण वर्ग संख्याएँ हैं? हम कैसे जानते हैं?
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 1069
(vi) 2061
पाँच ऐसी संख्याएँ लिखिए जिनके इकाई स्थान को देखकर आप बता सकें कि ये संख्याएँ वर्ग संख्याएँ नहीं हैं।
हल:
(i) 1057 - संख्या 1057 का इकाई स्थान का अंक 0, 1, 4, 5, 6 या 9 नहीं है। अतः यह पूर्ण वर्ग संख्या नहीं है।

(ii) 23453 - संख्या 23453 के इकाई स्थान पर 0, 1, 4, 5, 6 या 9 नहीं है। अतः यह पूर्ण वर्ग संख्या नहीं है।

(iii) 7928 - संख्या 7928 के इकाई स्थान पर 0, 1, 4, 5, 6 या 9 नहीं है। अतः यह पूर्ण वर्ग संख्या नहीं हो सकती है।

(iv) 222222 - संख्या 222222 के इकाई के स्थान पर 0, 1, 4, 5, 6 या 9 नहीं है। अतः यह पूर्ण वर्ग संख्या नहीं हो सकती है।

(v) 1069 - संख्या 1069 के इकाई स्थान पर 9 है। अतः यह पूर्ण वर्ग संख्या हो सकती है और नहीं भी हो सकती है।
लेकिन 3² = 32 × 32 = 1024
और 33² = 33 × 33 = 1089
∴ 1069 एक पूर्ण वर्ग संख्या नहीं है।

(vi) 2061 - संख्या 2061 के इकाई स्थान पर 1 है। अतः यह पूर्ण वर्ग संख्या भी हो सकती है और नहीं भी हो सकती है। लेकिन 452 = 45 × 45 = 2025
और 462 = 46 × 46 = 2116
∴ 2061 एक पूर्ण वर्ग संख्या नहीं है।
पाँच संख्याएँ जिनके इकाई स्थान को देखकर हम पता कर सकते हैं कि ये वर्ग संख्याएँ नहीं हैं, वे हैं 22, 43, 57, 268 और 193.

प्रश्न 2.
पाँच ऐसी संख्याएँ लिखिए जिनके इकाई स्थान को देखकर आप नहीं बता सकते कि वे वर्ग संख्याएँ हैं या नहीं?
हल:
ऐसी पाँच संख्याएँ जिनके इकाई स्थान को देखकर हम नहीं बता सकते कि ये वर्ग संख्याएँ हैं या नहीं, वे हैं 1331, 2744, 3375, 17576 और 24389

(पृष्ठ 97-II)

प्रश्न 1.
123²,77²,82², 161², 109² में से कौनसी संख्या अंक 1 पर समाप्त होगी?
हल:
हम जानते हैं कि यदि संख्या के इकाई स्थान का अंक 1 अथवा 9 है, तो इनके वर्ग 1 पर समाप्त होते हैं। अतः 161² और 109² के अंक एक पर समाप्त होंगे।

(प्रयास कीजिए - पृष्ठ 98-I)

प्रश्न 1.
निम्नलिखित में से कौनसी संख्याओं के इकाई स्थान पर 6 अंक होगा
(i) 19²
(ii) 24²
(iii) 26²
(iv) 36²
(v) 34²
हल:
जिस संख्या का इकाई अंक 4 या 6 होता है, उसकी वर्ग संख्या के इकाई स्थान पर 6 अंक होता है। इस आधार पर हम उक्त संख्याओं की जाँच करेंगे।
(i) क्योंकि 19, 4 या 6 पर समाप्त नहीं होता है। अतः 192 के इकाई स्थान पर 6 अंक नहीं होगा।
(ii) क्योंकि 24,4 पर समाप्त होता है। अतः 242 के इकाई स्थान पर 6 होगा।
(iii) क्योंकि 26, 6 पर समाप्त होता है। अतः 262 के इकाई स्थान पर 6 होगा।
(iv) क्योंकि 36, 6 पर समाप्त होता है। अतः 362 के इकाई स्थान पर 6 होगा।
(v) क्योंकि 34, 4 पर समाप्त होता है। अत: 34 के इकाई स्थान पर 6 होगा।

(पृष्ठ 98-II)

प्रश्न 1.
निम्नलिखित संख्याओं के वर्ग करने पर उनके इकाई स्थान पर क्या होगा?
(i) 1234
(ii) 26387
(iii) 52698
(iv) 99880
(v) 21222
(vi) 9106
हल:

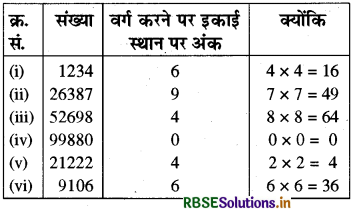
(पृष्ठ 98-III)

प्रश्न 1.
निम्नलिखित में से किन संख्याओं के वर्ग विषम संख्या/सम संख्या होंगे? क्यों?
(i) 727
हल:
क्योंकि 727 एक विषम संख्या है। अतः इसका वर्ग भी विषम संख्या होगी।

(ii) 158
हल:
क्योंकि 158 एक सम संख्या है। अतः इसका वर्ग भी सम संख्या होगी।

(iii) 269
हल:
क्योंकि 269 एक विषम संख्या है। अतः इसका वर्ग भी विषम संख्या होगी।

(iv) 1980
हल:
क्योंकि 1980 एक सम संख्या है। अतः इसका वर्ग भी सम संख्या होगी।

प्रश्न 2.
निम्नलिखित संख्याओं के वर्ग में शून्यों की संख्या क्या होगी?
(i) 60
हल:
60² में दो शून्य होंगे।

(ii) 400
हल:
400² में चार शून्य होंगे।

(प्रयास कीजिए - पृष्ठ 100)

प्रश्न 1.
9² और 10² के बीच कितनी प्राकृत संख्याएँ हैं? 11² और 12² के बीच भी प्राकृत संख्याओं की संख्या बताइए।
हल:
9² और 10² के बीच 2n अर्थात् 2 × 9 = 18 प्राकृत संख्याएँ हैं।
11² और 12² के बीच 2 × 11 = 22 प्राकृत संख्याएँ हैं।

प्रश्न 2.
निम्नलिखित संख्याओं के यग्मों के बीच की संख्या बताइए जो वर्ग संख्याएँ नहीं हैं।
(i) 100² और 101²
हल:
100² और 101² के बीच 2n अर्थात् 2 × 100 = 200 संख्याएँ हैं, जो वर्ग संख्याएँ नहीं हैं।

(ii) 90² और 91²
हल:
90² और 91² के बीच 2n अर्थात् 2 × 90 = 180 संख्याएँ हैं, जो वर्ग संख्याएँ नहीं हैं।

(iii) 1000² और 1001²
हल:
1000² और 1001² के बीच 2n अर्थात् 2 × 1000 = 2000 संख्याएँ हैं, जो वर्ग संख्याएँ नहीं हैं।

(प्रयास कीजिए - पृष्ठ 101-I)

प्रश्न 1.
निम्नलिखित संख्याओं में प्रत्येक पूर्ण वर्ग संख्याएँ हैं अथवा नहीं?
(i) 121
(ii) 55
(iii) 81
(iv) 49
(v) 69
हल:
हम जानते हैं कि पहली n विषम प्राकृत संख्याओं का योग n होता है। अतः उक्त संख्याओं में से 1, 3, 5, 7... को क्रम से घटाएंगे।
(i) दी गई संख्या 121 में से क्रमशः 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 घटाएंगे।
121 - 1 = 120, 120 - 3 = 117, 117 - 5 = 112, 112 - 7 = 105, 105 - 93 = 96, 96 - 11 = 85, 85 - 13 = 72, 72 - 15 = 57, 57 - 17 = 40, 40 --19 = 21, 21 - 21 = 0
इसका अर्थ है 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
∴ 121 एक पूर्ण वर्ग संख्या है।

(ii) दी गई संख्या 55 में से क्रमशः 1, 3, 5, 7, 9, 11, 13, 15 घटाएँगे।
55 - 1 = 54, 54 - 3 = 51, 51 - 5 = 46, 46 - 7 = 39, 39 - 9 = 30,30/- 11 = 19, 19 - 13 = 6, 6- 15 = -9 यह दर्शाता है कि 55 को 1 से प्रारम्भ होने वाली विषम संख्याओं के योग के रूप में व्यक्त नहीं कर सकते हैं।
∴ 55 एक पूर्ण वर्ग संख्या नहीं है।।

(iii) दी गई संख्या 81 में से क्रमशः 1, 3, 5, 7, 9, 11, 13, 15, 17 घटाएँगे। 81 - 1 = 80, 80 - 3 = 77, 77 - 5 = 72, 72 - 7 = 65, 65 - 9 = 56, 56 - 11 = 45, 45 - 13 = 32, 32 - 15 = 17, 17 - 17 = 0
इसका अर्थ हैं 81 = 1+ 3 +5 +7+9+ 11+ 13 + 15 + 17
∴ 81 एक पूर्ण वर्ग संख्या है।

(iv) दी गई संख्या 49 में से क्रमशः 1, 3, 5, 7, 9, 11, 13 घटाएंगे।
49 - 1 = 48, 48 - 3 = 45, 45 - 5 = 40, 40 - 7 = 33, 33 - 9 = 24, 24 - 11 = 13, 13 - 13 = 0
इसका अर्थ है 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13
∴ 49 एक पूर्ण वर्ग संख्या है।

(v) दी गई संख्या 69 में से क्रमशः 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 घटाइए।
69 - 1 = 68, 68 - 3 = 65, 65 - 5 = 60, 60 - 7 = 53, 53 - 9 = 44, 44 - 11 = 33, 33 - 13 = 20, 20 - 17 = 3, 3 - 19 = -16 यह दर्शाता है कि 69 को 1 से आरम्भ होने वाली विषम संख्याओं के योग के रूप में व्यक्त नहीं कर सकते हैं।
∴ 69 एक पूर्ण वर्ग संख्या नहीं है।

(पृष्ठ 101-II)

प्रश्न 1.
निम्नलिखित संख्याओं को दो क्रमागत पूर्णांकों के योग के रूप में लिखिए
(i) 212
हल:
21² = 441 = 220 + 221, जो दो क्रमागत पूर्णांकों के योग को दर्शाता है।
[∵ \(\frac{21^{2}-1}{2}\) = 220 और \(\frac{21^{2}+1}{2}\) = 221]

(ii) 132
हल:
13² = 169 = 84 + 85 जो, दो क्रमागत पूर्णांकों के योग को दर्शाता है।
[∵ \(\frac{13^{2}-1}{2}\) = 84 और \(\frac{13^{2}+1}{2}\) = 85]

(iii) 112
हल:
112 = 121 = 60 + 61, जो दो क्रमागत पूर्णांकों के योग को दर्शाता है।
[∵ \(\frac{11^{2}-1}{2}\) = 60 और \(\frac{11^{2}+1}{2}\) = 61]

(iv) 192
हल:
192 = 361 = 180 + 181, जो दो क्रमागत पूर्णांकों के योग को दर्शाता है।
[∵ \(\frac{19^{2}-1}{2}\) = 180 और \(\frac{19^{2}+1}{2}\) = 181]

प्रश्न 2.
क्या आप सोचते हैं कि इसका विलोम सत्य है अर्थात् क्या दो क्रमागत धनात्मक पूर्णांकों का योग एक पूर्ण वर्ग होता है? अपने उत्तर के पक्ष में एक उदाहरण दीजिए।
हल:
नहीं, दो क्रमागत धनात्मक पूर्णांकों का योग सदैव एक पूर्ण वर्ग नहीं होता है। उदाहरण के तौर पर 3 + 4 = 7, 11 + 12 = 23 इत्यादि। यहाँ 3 और 4 तथा 11 और 12 क्रमागत धनात्मक पूर्णांक हैं, परन्तु इनका योग 7 तथा 23 पूर्ण वर्ग संख्याएँ नहीं

[प्रयास कीजिए - पृष्ठ 102-I]

प्रश्न 1.
निम्न प्रतिरूप का उपयोग करते हुए नीचे दी गई संख्याओं की वर्ग संख्याएँ लिखिए

(i) 111111²
(ii) 1111111²
हल:
(i) 111111² = 1 2 3 4 5 6 5 4 3 2 1
(ii) 1111111² = 1 2 3 4 5 6 7 6 5 4 3 2 1

(पृष्ठ 102-II)

प्रश्न 1.
दिए गए प्रतिरूप का उपयोग करते हुए क्या आप निम्नलिखित संख्याओं का वर्ग ज्ञात कर सकते हैं?
(i) 66666672
(ii) 666666672 प्रतिरूप
7² = 49
67² = 4489
667² = 444889
6667² = 44448889
66667² = 4444488889
666667² = 444444888889
हल:
(i) 6666667² = 44444448888889
(ii) 66666667² = 4444444488888889

(प्रयास कीजिए - पृष्ठ 104)

प्रश्न 1.
निम्नलिखित संख्याओं के वर्ग ज्ञात कीजिए जिनके इकाई अंक 5 हैं
(i) 15
हल:
15² = (1 × 2) सौ + 25
= 200 + 25 = 225

(ii) 95
हल:
95² = (9 × 10) सौ + 25
= 9000 + 25 = 9025

(iii) 105
हल:
105² = (10 × 11) सौ + 25.
= 11000 + 25 = 11025

(iv) 205
हल:
205² = (20 × 21) सौ + 25
= 42000 + 25 = 42025

(प्रयास कीजिए - पृष्ठ 106)

प्रश्न 1.
(i) 11² = 121. 121 का वर्गमल क्या है?
हल:
क्योंकि 11² = 121, अतः 121 का वर्गमूल 11

(ii) 14² = 196. 196 का वर्गमूल क्या है?
हल:
क्योंकि 14² = 196, अतः 196 का वर्गमूल 14 है।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 106)

प्रश्न 1.
(-1)² = 1. क्या 1 का वर्गमूल है -1?
हल:
हाँ, -1, 1 का वर्गमूल है।
1 के दो वर्गमूल हैं + 1 तथा -1

प्रश्न 2.
(-2)² = 4, क्या 4 का वर्गमूल है -2?
हल:
हाँ, 4 का वर्गमूल -2 है।

प्रश्न 3.
(-9)² = 81. क्या 81 का वर्गमूल है - 9?
हल:
हाँ, 81 का वर्गमूल -9 है।

(प्रयास कीजिए - पृष्ठ 107)

प्रश्न 1.
से प्रारम्भ होने वाली विषम संख्याओं को बारबार घटाने पर प्राप्त निम्नलिखित संख्याएँ पूर्ण वर्ग हैं या नहीं? यदि यह संख्या पूर्ण वर्ग है तो इसके वर्गमूल ज्ञात कीजिए।
(i) 121
हल:
121 में से हम क्रमशः 1 से प्रारम्भ होने वाली विषम संख्याओं को घटाएँगे।
121 - 1 = 120
120 - 3 = 117
117 - 5 = 112
112 - 7 = 105
105 - 9 = 96
95 - 11 = 85
85 - 13 = 72
72 - 15 = 57
57 - 17 = 40
40 - 19 = 21
21 - 21 = 0
हमें 1 से 21 तक 11 पद प्राप्त होते हैं और 121 को 1 से प्रारम्भ करके क्रमागत विषम संख्याओं के योग के रूप में व्यक्त कर सकते हैं। अतः 121 एक पूर्ण वर्ग है और \(\sqrt{121}\) = 11

(ii) 55
हल:
55 में से 1 से प्रारम्भ करके विषम संख्याओं को घटाएंगे
55 - 1 = 54
54 - 3 = 51
51 - 5 = 46
46 - 7 = 39
39 - 9 = 30
30 - 11 = 19
19 - 13 = 6,
6 - 15 = -9
यह दर्शाता है कि हम 55 को 1 से प्रारम्भ होने वाली क्रमागत संख्याओं को योग के रूप में व्यक्त नहीं कर सकते
∴ 55 एक पूर्ण वर्ग नहीं है।

(iii) 36
हल:
36 में से हम क्रमशः 1 से प्रारम्भ करके विषम संख्याओं को घटाएंगे
36 - 1 = 35
35 - 3 = 32
32 - 5 = 27
27 - 7 = 20
20 - 9 = 11
11 - 11 = 0
हमें 1 से 11 तक 6 पद प्राप्त होते हैं और 36 को क्रमागत विषम संख्याओं के योग के रूप में व्यक्त कर सकते हैं।
अतः 36 पूर्ण वर्ग है और \(\sqrt{36}\) = 6

(iv) 49
हल:
49 में से हम 1 से प्रारम्भ करके क्रमशः विषम संख्याओं को घटाएँगे
49 - 1 = 48
48 - 3 = 45
45 - 5 = 40
40 - 7 = 33
33 - 9 = 24
24 - 11 = 13
13 - 13 = 0
हमें 1 से 13 तक 7 पद प्राप्त होते हैं और 49 को 1 से प्रारम्भ होने वाली क्रमागत विषम संख्याओं के योग के रूप में व्यक्त कर सकते हैं।
अतः 49 एक पूर्ण वर्ग है और \(\sqrt{49}\) = 7.

(v) 90
हल:
90 में से हम 1 से प्रारम्भ करके क्रमशः विषम संख्याओं को घटाएँगे
90 - 1 = 89
89 - 3 = 86
86 - 5 = 81
81 - 7 = 74
74 - 9 = 65
65 - 11 = 54
54 - 13 = 41
41 - 15 = 26
26 - 17 = 9
9 - 19 = -10
यह दर्शाता है कि हम 90 को 1 से प्रारम्भ होने वाली विषम संख्याओं के योग के रूप में व्यक्त नहीं कर सकते हैं।
∴ 90 एक पूर्ण वर्ग नहीं है।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 111)

प्रश्न 1.
क्या हम कह सकते हैं कि एक पूर्ण वर्ग संख्या में यदि अंक है तो उसके वर्गमूल में \(\frac{n}{2}\), अंक होंगे। यदि n सम है या \(\frac{(n+1)}{2}\) होंगे यदि विषम है?
हल:
हाँ, हम कह सकते हैं कि यदि एक पूर्ण वर्ग संख्या में n अंक है, तो इसके वर्गमूल में
(i) \(\frac{n}{2}\) अंक होंगे, यदि n सम है और
(ii) \(\frac{n}{2}\) अंक होंगे, यदि विषम है।
इसे निम्न उदाहरण से स्पष्ट किया जा सकता है
\(\sqrt{361}\) =19, \(\sqrt{1296}\) = 36, \(\sqrt{17161}\) = 131, \(\sqrt{194481}\) = 441 आदि।

(प्रयास कीजिए - पृष्ठ 112)

प्रश्न 1.
निम्नलिखित संख्याओं के वर्गमूल में अंकों की संख्या को गणना के बिना ज्ञात कीजिए
(i) 25600
(ii) 100000000
(iii) 36864
हल:
(i) क्योंकि 25600 में 5 अंक हैं, अतः \(\sqrt{25600}\) में \(\frac{5+1}{2}\) अर्थात् 3 अंक होंगे।
(ii) क्योंकि 100000000 में 9 अंक हैं, अतः इसके - वर्गमूल में \(\frac{9+1}{2} \)अर्थात् 5 अंक होंगे।
(iii) क्योंकि 36864 में 5 अंक हैं, अतः इसके वर्गमूल में \(\frac{5+1}{2}\) अर्थात् 3 अंक होंगे।

(प्रयास कीजिए - पृष्ठ 115)

प्रश्न 1.
निम्नलिखित संख्याओं के निकटतम पूर्ण संख्याओं का अनुमान लगाइए
(i) \(\sqrt{80}\)
हल:
\(\sqrt{80}\) हम जानते हैं 64< 80 < 81
अतः 8 < \(\sqrt{80}\) < 9
∵ 81, 64 की अपेक्षा 80 के अधिक नजदीक है।
∴ \(\sqrt{80}\) लगभग 9 है।

(ii) \(\sqrt{1000}\)
हल:
\(\sqrt{1000}\) हम जानते हैं
31² = 961 और 32² = 1024
अतः 31 < \(\sqrt{1000}\) < 32
∵ 1000, 961 की अपेक्षा 1024 के अधिक नजदीक है।
∴ \(\sqrt{1000}\) लगभग 32 है।

(iii) \(\sqrt{350}\)
हल:
\(\sqrt{350}\) हम जानते हैं 18² = 324 और 19² = 361
अतः 18 < \(\sqrt{350}\) < 19
∵ 350, 324 की अपेक्षा 361 के अधिक नजदीक है।
∴ \(\sqrt{350}\) लगभग 19 है।

(iv) \(\sqrt{500}\)
हल:
\(\sqrt{500}\) हम जानते हैं 22² = 484 और 23² = 529
22 < \(\sqrt{500}\) < 23
∵ 500, 529 की अपेक्षा 484 के अधिक नजदीक है।
∴ \(\sqrt{500}\) लगभग 22 है।