RBSE Solutions for Class 8 Maths Chapter 6 Square and Square Roots Ex 6.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 6 Square and Square Roots Ex 6.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 6 Square and Square Roots Ex 6.1

Question 1.
What will be the unit digit of the squares of the following numbers?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 26387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
Answer:
The unit digit of the squares of the given numbers is shown in the table :

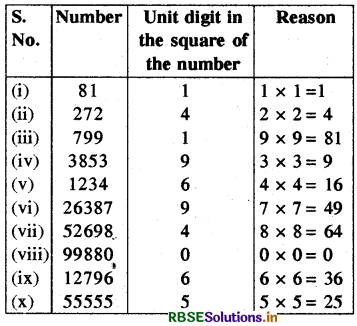
Question 2.
The following numbers are obviously not perfect squares. Give reason,
(i) 1057
Answer:
A number that ends either with 2, 3, 7 or 8 cannot be a perfect square. Also, a number that ends with odd number of zero(s) cannot be a perfect square.
∵ The given number 1057 ends with 7, so it cannot be a perfect square.

(ii) 23453
Answer:
∵ 23453 ends with 3, so it cannot be a perfect square.

(iii) 7928
Answer:
∵ 7928 ends with 8, so it cannot be a perfect square.

(iv) 222222
Answer:
∵ 222222 ends with 2, so it cannot be a perfect square.

(v) 64000
Answer:
∵ 64000 ends with an odd number of zeros, so it cannot be a perfect square.

(vi) 89722
Answer:
∵ 89722 ends with 2, so it cannot be a perfect square.

(vii) 222000
Answer:
∵ 222000 ends with an odd number of zeros, so it cannot be a perfect square.

(viii) 505050
Answer:
∵ 505050 ends with an odd number of zeros, so it cannot be a perfect square.

Question 3.
The squares of which of the following would be odd numbers?
(i) 431
Answer:
431 is an odd, so its square must be odd.

(ii) 2826
Answer:
2826 in an even, so its square must be even.

(iii) 7779
Answer:
7779 is an odd, so its square must be odd.

(iv) 82004
Answer:
82004 is an even, so its square must be even.

Question 4.
Observe the following pattern and find the missing digits.
11² = 121
101² = 10201
1001² = 1002001
100001² = 1 ............... 2 ................... 1
10000001² = .............................
Answer:
100001² = 10000200001
10000001²= 100000020000001

Question 5.
Observe the following pattern and supply the missing numbers.
112² = 121
101² = 10201
10101² = 102030201
1010101² = _________
__________² = 10203040504030201
Answer:
The missing numbers are
1010101² = 1020304030201
101010101² = 10203040504030201

Question 6.
Using the given pattern, find the missing numbers.
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + ....² = 21²
5² + ....² + 30² = 31²
6² + 7² + .........² = ......²
Answer:
The missing numbers are:
4² + 5² + 20² = 21²
5² + 6² + 30² = 31²
6² + 7² + 42² = 43²

Question 7.
Without adding, find the sum.
(i) 1+ 3 + 5 + 7 + 9
Answer:
1 + 3 + 5+ 7 + 9
= Sum of first 5 odd numbers = 5² = 25

(ii) 1 + 3 + 5+ 7 + 9 + 11 + 13 + 15 + 17 + 19
Answer:
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
= Sum of first 10 odd numbers = 10² = 100

(iii) 1+3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Answer:
1 + 3 + 5 + 7 + 9+11 + 13 + 15 + 17 + 19 + 21 + 23
= Sum of first 12 odd numbers = 12² = 144

Question 8.
(i) Express 49 as the sum of 7 odd numbers.
Answer:
49 = 7² = 1 + 3 + 5 + 7 + 9 + 11 + 13

(ii) Express 121 as the sum of 11 odd numbers.
Answer:
121 = 11²
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21

Question 9.
How many numbers lie between squares of the following numbers?
(i) 12 and 13
Answer:
There are 24 (i.e. 2 × 12) numbers lie between 12² and 13².

(ii) 25 and 26
Answer:
There are 50 (i.e. 2 × 25) numbers lie between 25² and 26².

(iii) 99 and 100
Answer:
There are 198 (i.e. 2 × 99) numbers lie between 99² and 100².