RBSE Solutions for Class 8 Maths Chapter 5 आँकड़ो का प्रबंधन Ex 5.3

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 5 आँकड़ो का प्रबंधन Ex 5.3 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 5 आँकड़ो का प्रबंधन Ex 5.3

प्रश्न 1.
इन प्रयोगों में आप जो परिणाम देख सकते हैं, उन्हें लिखिए-
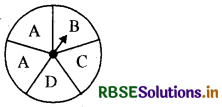
(a) पहिए को घुमाना।
(b) दो सिक्कों को एक साथ उछालना।

हल:
(a) पहिए को घुमाने से प्राप्त परिणाम होंगे A, B, C और D
(b) जब दो सिक्के उछालते हैं तो प्राप्त परिणाम होंगे HH, HT, TH और TT (संकेतः H = Head, T = Tail)

प्रश्न 2.
जब एक पासे को फेंका जाता है, तब निम्नलिखित प्रत्येक घटना से प्राप्त होने वाले परिणामों को लिखिए
(i) (a) एक अभाज्य संख्या
(b) एक अभाज्य संख्या नहीं
हल:
एक पासे को एक बार फेंकने पर प्राप्त परिणाम
(a) एक अभाज्य संख्या 2, 3 और 5
(b) एक अभाज्य संख्या नहीं 1, 4 और 6

(ii) (a) 5 से बड़ी एक संख्या
(b) 5 से बड़ी संख्या नहीं।
हल:
(a) 5 से बड़ी एक संख्या 6 है।
(b) 5 से बड़ी संख्या नहीं 1, 2, 3, 4 और 5

प्रश्न 3.
ज्ञात कीजिए| (a) (प्रश्न 1 (a) में) सूचक के D पर रुकने की प्रायिकता।
(b) अच्छी प्रकार से फेंटी हई 52 ताशों की एक गड्डी में से 1 इक्का प्राप्त करने की प्रायिकता।
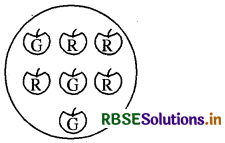
(c) एक लाल सेब प्राप्त करने की प्रायिकता (दी आकृति से देखिए।)

हल:
(a) 5 त्रिज्य खंडों में से सूचक के किसी एक खण्ड में रुकने की पाँच विधियाँ हैं।
∴ कुल परिणाम = 5, घुमाने वाले पहिए में एक 'D' है।
∴ संभावित परिणाम = 1
∴ वांछित प्रायिकता = 1

(b) 52 पत्तों में से एक पत्ता 52 विधियों से प्राप्त करते हैं।
∴ कुल परिणाम = 52
52 पत्तों की गड्डी में 4 इक्के उनमें से एक इक्के को 4 विधियों से खींच सकते हैं।
∴ संभावित परिणाम = 4
अत: वांछित प्रायिकता = \(\frac{4}{52}\) = \(\frac{1}{13}\) उत्तर

(c) 7 सेबों में से एक लाल सेब 7 विधियों से खींच सकते
∴ कुल परिणाम = 7
कुल 4 लाल सेब हैं। इनमें से कोई एक लाल सेब 4 विधियों से खींच सकते हैं।
∴ संभावित परिणाम = 4
अतः वांछित प्रायिकता = \(\frac{4}{7}\)

प्रश्न 4.
10 पृथक् पर्चियों पर 1 से 10 तक संख्याएँ लिखी हुई हैं (एक पर्ची पर एक संख्या), उन्हें एक बक्स में रखकर अच्छी प्रकार से मिला दिया जाता है। बक्स के अन्दर से बिना देखे एक पर्ची निकाली जाती है। निम्नलिखित की प्रायिकता क्या है?
(i) संख्या 6 प्राप्त करना।
(ii) 6 से छोटी एक संख्या प्राप्त करना।
(iii) 6 से बड़ी एक संख्या प्राप्त करना।
(iv) 1 अंक की एक संख्या प्राप्त करना।
हल:
10 पर्चियों में से 1 पर्ची 10 विधियों से खींच सकते हैं। अतः कुल परिणाम = 10
(i) 6 प्राप्त करने की घटना अर्थात् यदि हम 6 संख्या वाली पर्ची प्राप्त करेंगे।
अतः अनुकूल परिणाम = 1
∴ वांछित प्रायिकता = \(\frac{1}{10}\)

(ii) 6 से छोटी एक संख्या प्राप्त करने की घटना अर्थात् यदि हमें परिणाम में 1, 2, 3, 4, 5 वाली पर्ची प्राप्त हो।
अतः अनुकूल परिणाम = 5
∴ वांछित प्रायिकता = \(\frac{5}{10}\) = \(\frac{1}{2}\)

(iii) 6 से बड़ी एक संख्या प्राप्त करने की घटना अर्थात् जब पर्ची पर 7, 8, 9, 10 लिखा हो।
अतः अनुकूल परिणाम = 4
∴ वांछित प्रायिकता = \(\frac{4}{10}\) = \(\frac{1}{2}\)

(iv) एक अंक वाली एक संख्या प्राप्त करने की घटना अर्थात् यदि हमें पर्ची पर 1, 2, 3, 4, 5, 6, 7, 8, 9 लिखा प्राप्त हो।
अतः अनुकूल परिणाम = 9
∴ वांछित प्रायिकता = \(\frac{9}{10}\)

प्रश्न 5.
यदि आपके पास 3 हरे त्रिज्यखण्ड, 1 नीला त्रिज्यखण्ड और 1 लाल त्रिज्यखण्ड वाला एक घूमने वाला पहिया है, तो एक हरा त्रिज्यखण्ड प्राप्त करने की प्रायिकता क्या है? ऐसा त्रिज्यखण्ड प्राप्त करने की प्रायिकता क्या है, जो नीला न हो?
हल:
5 त्रिज्यखण्डों में से सूचक किसी एक खण्ड पर पाँच विधियों से रुकेगा।
∴ कुल परिणाम = 5
इनमें 3 हरे रंग के त्रिज्यखण्डों में से एक 3 विधियों से प्राप्त होगा।
∴ अनुकूल परिणाम = 3
अत: वांछित प्रायिकता = 3
आगे घुमाने वाले पहिए पर 4 त्रिज्यखण्ड नीले नहीं हैं जो 4 विधियों से प्राप्त होंगे।
अतः वांछित प्रायिकता = \(\frac{4}{5}\) उत्तर

प्रश्न 6.
प्रश्न 2 में दी हुई घटनाओं की प्रायिकताएँ ज्ञात कीजिए।
हल:
पासे को एक बार फेंकने पर इसकी सतह पर 1, 2, 3, 4, 5, 6 तक लिखी संख्याओं में से कोई एक संख्या प्राप्त होगी।
अतः कुल परिणाम = 6
(i) माना A अभाज्य संख्याओं को दर्शाता है। स्पष्ट है कि A तब ही आएगा जब हमें 2, 3, 5 प्राप्त हों।
∴ अनुकूल परिणाम = 3
अतः, P(A) = \(\frac{3}{6}\) = \(\frac{1}{2}\) उत्तर

(ii) माना A अभाज्य संख्या प्राप्त नहीं करने को दर्शाता है। स्पष्ट है A घटना होगी जब हमें 1, 4, 6 प्राप्त हों।
∴ अनुकूल परिणाम = 3
अतः, P(A) = \(\frac{3}{6}\) = \(\frac{1}{2}\) उत्तर

(iii) 5 से बड़ी संख्या प्राप्त करने की घटना जब हमें 6 प्राप्त होगा तब ही होगी।
∴ अनुकूल परिणाम = 1
अतः, वांछित प्रायिकता = \(\frac{1}{6}\) उत्तर

(iv) 5 से बड़े अंक प्राप्त नहीं करने की घटना तब होगी जब हमें 1, 2, 3, 4, 5 प्राप्त होंगे।
∴ अनुकूल प्रायिकता = 5
अतः वांछित प्रायिकता = \(\frac{5}{6}\) उत्तर