RBSE Solutions for Class 8 Maths Chapter 4 प्रायोगिक ज्यामिती Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 4 प्रायोगिक ज्यामिती Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 4 प्रायोगिक ज्यामिती Intext Questions

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 64)

प्रश्न 1.
अरशद के पास एक चतुर्भुज ABCD की पाँच माप हैं। ये माप AB = 5 cm, ZA = 50°, AC = 4 cm, BD = 5 cm और AD = 6 cm हैं। क्या वह इन मापों से एक अद्वितीय चतुर्भुज बना सकता है? अपने उत्तर के कारण दीजिए।
उत्तर:
दिए गए आँकड़ों से वह चतुर्भुज ABCD नहीं बना सकता है जिसके निम्नलिखित कारण हैं

• यदि वह पहले विकर्ण BD लेता है तो पहला ΔABD बना लेता है परन्तु दूसरा ΔBCD नहीं बना सकता क्योंकि इसकी केवल .एक भुजा दी गई है।
• यदि वह पहले विकर्ण AC लेता है तो ΔACD और ΔABC को बनाने के लिए पर्याप्त आँकड़े नहीं हैं।

[पृष्ठ 66]

प्रश्न 1.
(i) हमने देखा कि एक चतुर्भुज की पाँच मायों से एक अद्वितीय चतुर्भुज की रचना की जा सकती है। क्या आप सोचते हैं कि चतुर्भुज की किन्हीं पाँच मापों से ऐसी रचना की जा सकती है?
उत्तर:
एक चतुर्भुज के बनाने के लिए निम्नलिखित पाँच मापों का होना आवश्यक है|

• जब चार भुजाएँ और एक विकर्ण दिया हो।
• जब दो विकर्ण और तीन भुजाएँ दी गई हों।
• दो आसन्न भुजाएँ तथा तीन कोण दिए गए हों।
• जब तीन भुजाएँ तथा इनके बीच दो कोण दिए गए हों।
• जब चार भुजाएँ तथा एक कोण दिया गया हो।

(ii) क्या आप एक समान्तर चतुर्भुज BATS की रचना कर सकते हैं जिसमें BA = 5 cm, AT = 6 cm और AS = 6.5 cm हो? क्यों?
उत्तर:
हाँ, समान्तर चतुर्भुज BATS को दिए गए आँकड़ों के साथ बना सकते हैं क्योंकि इनसे दो ABAS और ASAT बना सकते हैं।

(iii) क्या आप एक सम चतुर्भुज (Rhombus) ZEAL की रचना कर सकते हैं जिसमें ZE = 3.5 cm, विकर्ण EL = 5 cm है? क्यों?
उत्तर:
हाँ, दिए गए आँकड़ों द्वारा सम चतुर्भुज ZEAL खींच सकते हैं क्योंकि इनसे बनने वाले दो ΔZEL और ΔLEA बना सकते हैं।

(iv) एक विद्यार्थी एक चतुर्भुज PLAY की रचना करने का प्रयास करता है जिसमें PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm और LY = 6 cm है, परन्तु वह इसकी रचना नहीं कर सका। कारण बताइए। [संकेत-एक कच्ची आकृति की सहायता से चर्चा कीजिए।
उत्तर:
यहाँ दिए गए आँकडों द्वारा खींची गई रफ आकृति दी 14.5 cm गई है।

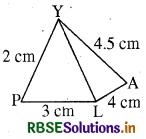
इसके अनुसार-
PY + PL ≯ YL (2 + 3 ≯ 6) 
अतः ΔPLY की रचना संभव नहीं है। अतः वह इसे खींच नहीं पाता।

[पृष्ठ 68]

प्रश्न 1.
पाठ्यपुस्तक में दिए गए उदाहरण 2 में क्या हम पहले ΔABD खींचकर उसके बाद चतुर्थ बिन्दु C को ज्ञात करके चतुर्भुज की रचना कर सकते हैं?
हल:
क्योंकि भुजा AB का परिमाप नहीं दिया गया है।

हम बिन्दु B को अंकित नहीं कर सकते हैं इसलिए सर्वप्रथम ΔABD खींचकर हम समान्तर चतुर्भुज की रचना नहीं कर सकते हैं ।
अतः इस तरह चतुर्थ बिन्दु C ज्ञात नहीं किया जा सकता है।

प्रश्न 2.
क्या आप एक चतुर्भुज PQRS की रचना कर सकते हैं जिसमें PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8cm और SQ = 4 cm है? अपने उत्तर की पुष्टि कीजिए।
हल:
सबसे पहले चतुर्भुज PORS की कच्ची आकृति खींची।

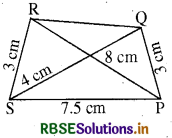
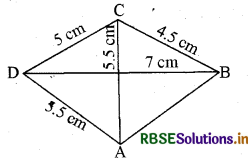
दिए गए आँकड़ों के आधार पर चतुर्भुज PQRS की रचना नहीं कर सकते क्योंकि Δ QSP नहीं बना सकते क्योंकि 
SQ + QP ≯ SP

[पृष्ठ 69]

प्रश्न 1.
यदि हमें M पर 75° माप के स्थान पर 100° की माप दी गई हो, तो क्या आप पाठ्यपुस्तक के उदाहरण 3 में बताए गए चतुर्भुज MIST की रचना कर सकते हैं?
उत्तर:
हाँ, M पर 75° के स्थान पर 100° लेकर चतुर्भुज MIST की रचना कर सकते हैं।

प्रश्न 2.
क्या आप एक चतुर्भुज PLAN की रचना कर सकते हैं, यदि PL = 6 cm, LA = 9.5 cm, ∠P = 75°, ∠L = 150° और ∠A = 140° है?
हल:
क्योंकि ∠P = 75°, ∠L = 150° और ∠A = 140°
∠P + ∠L + ∠A = 75°+ 150° + 140° = 365°.
अतः चतुर्भुज PLAN की रचना संभव नहीं है।

प्रश्न 3.
एक समान्तर चतुर्भुज में दो आसन्न भुजाओं की लम्बाइयाँ दी हुई हैं। क्या हमें रचना करने के लिए अभी भी कोणों की मापों की आवश्यकता है जैसा कि पाठ्यपुस्तक के उदाहरण 3 में दिया है?
हल:
एक अद्वितीय चतुर्भुज प्राप्त करने के लिए पाँच मापों की आवश्यकता होती है, लेकिन इस प्रश्न के अनुसार एक समान्तर चतुर्भुज की केवल दो आसन्न भुजाओं की लम्बाइयाँ दी गई हैं, अतः इस समान्तर चतुर्भुज की रचना करने के लिए अभी भी कोणों की मापों की आवश्यकता होगी। केवल प्रश्न में दी गई मापों से समान्तर चतुर्भुज की रचना असंभव है।

[पृष्ठ 71]

प्रश्न 1.
पाठ्य पुस्तक में दिए उदाहरण 4 में हमने सर्वप्रथम BC खींची। इसके स्थान पर दूसरे अन्य प्रारम्भ बिन्दु और कौनसे हो सकते हैं?
हल:
हम सर्वप्रथम AB अथवा CD भी खींच सकते थे। प्रश्न 2.हमने अभी तक चतुर्भुजों की रचना के लिए कोई पाँच मापों का प्रयोग किया।क्या एक चतुर्भुज की रचना करने के लिए पाँच मापों को अलग-अलग समुच्चय (अभी तक देखे गए मापों के अतिरिक्त) हो सकते हैं? अग्रलिखित समस्याएँ प्रश्नों के उत्तर देने में आपकी सहायता कर सकती हैं
(i) चतुर्भुज ABCD जिसमें AB =5 cm,B = 5.5 cm, CD = 4 cm, AD = 6 cm और ∠B = 80° है।
(ii) चतुर्भुज PQRS जिसमें PQ = 4.5 cm, ∠P = 70°, ∠Q = 100°, ∠R= 80° और ∠S = 110° है।
आप स्वयं कुछ और उदाहरणों की रचना कीजिए और एक चतुर्भुज की रचना के लिए आँकड़ों की पर्याप्तता/ अपर्याप्तता ज्ञात कीजिए।
हल:
(i) दिए गए आँकड़े चतुर्भुज की रचना के लिए हैं जब चार भुजाएँ और एक कोण दिए हैं।
(ii) इस दशा में चतुर्भुज नहीं खींच सकते हैं। नीचे एक अन्य दशा है जिसमें हम एक चतुर्भुज खींच सकते हैं। चतुर्भुज ABCD की रचना कीजिए जहाँ AB = 8 cm, BC = 4.5 cm, CD = 4 cm, ∠B = 60° और AB ∥ CD 

[पृष्ठ 72]
प्रयास कीजिए

प्रश्न 1.
आप एक आयत PQRS की रचना कैसे करेंगे यदि आप केवल PQ और QR की लम्बाई जानते
हल:
आयत की केवल दो आसन्न भुजाएँ दी गई । हैं। आयत के अन्य गुण निम्नांकित हैं

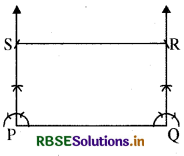
• इसकी सम्मुख भुजाएँ । समान होती हैं।
• प्रत्येक कोण 90° है। अतः पहले हम PQ रेखा खींचेंगे और तब ∠PQR = 90° इस प्रकार बनाएँगे कि QR (= दी गई लम्बाई) और ∠SPQ = 90° इस प्रकार बनाएंगे कि PS = QR | SR को मिलाएँगे और वांछित आयत PQRS प्राप्त हो जाएगा।

प्रश्न 2.
एक पतंग EASY की रचना कीजिए यदि AY = 8 cm, EY =4cm और SY = 6 cm है (आकृति देखें)। रचना के दौरान आपने पतंग के कौन-से गुणों का प्रयोग किया है?

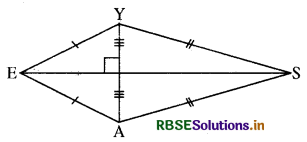
हल:
पतंग की रचना में हम पतंग के गुणों, पतंग की दो आसन्न भुजाएँ समान तथा सम्मुख भुजाएँ असमान होती हैं, का उपयोग करेंगे।
कोई भी उपयुक्त लम्बाई लेकर रेखा PQ खींचिए तथा इस पर कोई बिन्दु L लीजिए। L पर दर्शाए
अनुसार RU ⊥ PQ खींचिए। LR के साथ LU में से LA = LY = 4 cm काटिए। A को केन्द्र मानकर तथा 4 cm त्रिज्या लेकर एक चाप . लगाइए। Y को केन्द्र मानकर तथा 4 cm त्रिज्या लेकर दूसरी चाप लगाइए जो पहली चाप को E पर काटती है । EA और EY को मिलाइए। A को केन्द्र मानकर तथा 6 cm त्रिज्या लेकर F RS के दूसरी ओर एक चाप लगाइए। अब Y को केन्द्र मानकर 6 cm त्रिज्या लेकर चाप लगाइए जो पहली चाप को S पर काटती है। AS और YS को मिलाइए। इस प्रकार EASY वांछित पतंग है।