RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 3 चतुर्भुजों को समझना Intext Questions

(पाठगत प्रश्न - पृष्ठ 41)

प्रश्न 1.
निम्न आकृतियों का सुमेलन कीजिए

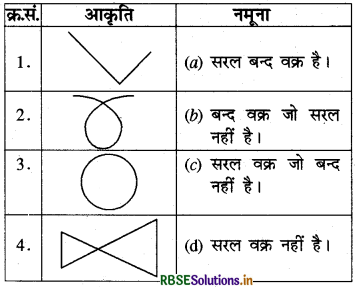
हल:
इनका सुमेलन निम्न प्रकार है

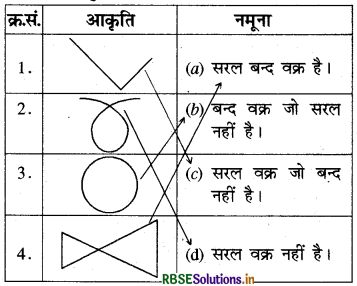
(इन्हें कीजिए। - पृष्ठ 44)

प्रश्न 1.
कोई एक चतुर्भुज, माना ABCD, लीजिए (आकृति के अनुसार)। एक विकर्ण खींचकर, इसे दो त्रिभुजों में बाँटिए। आप छः कोण 1,2,3,4,5 और 6 प्राप्त करते हैं। त्रिभुज के कोण-योग वाले गुणधर्म का उपयोग कीजिए और तर्क कीजिए कि कैसे ∠A, ∠B, ∠C तथा ∠D की मापों का योगफल 180° + 180° = 360° हो जाता है।

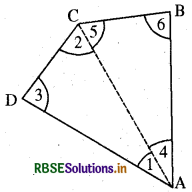
हल:
माना कि ABCD एक चतुर्भज है जिसका एक विकर्ण AC है। अतः
∠1 + ∠4 = ∠A
तथा ∠2 + ∠5 = ∠C 
हम जानते हैं कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है।

इस प्रकार ΔABC में, ∠4 + ∠5 + ∠B = 180° ....(1) 
तथा, ΔACD में, .
∠1 + ∠2 + ∠D = 180° .....(2)
(1) और (2) को जोड़ने पर 
(∠4 + ∠5 + ∠B) + (∠1 + ∠2 + ∠D) = 180° + 180° 
= (∠1 + ∠4) + ∠B + (∠2 + ∠5) + ∠D = 360°
∠A + ∠B + ∠C + ∠D = 360°
[∵ ∠1 + ∠4 = ∠A तथा ∠2 + ∠5 = ∠C] 
अतः, किसी चतुर्भज के चारों कोणों का योग 360° होता है।

प्रश्न 2.
किसी चतुर्भुज ABCD, की गत्ते वाली चार सर्वांगसम प्रतिलिपियाँ लीजिए जिनके कोण दर्शाए गए हैं [आकृति (i)], इन प्रतिलिपियों को इस प्रकार से व्यवस्थित कीजिए जिससे 21, 22, 23, 24 एक ही बिन्दु पर मिलें जैसा कि आकृति में दर्शाया गया है [ आकृति (ii)]

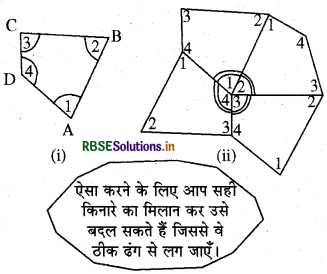
आप ∠1, ∠2, ∠3 तथा ∠4 के योगफल के बारे में क्या कह सकते हैं?
हल:
हम जानते हैं कि एक चतुर्भुज के चारों कोणों की मापों का योगफल 360° होता है। दिए गए चतुर्भुज ABCD 
∠A + ∠B + ∠C + ∠D = 360°
∴ m∠1 + m∠2 + m∠3 + m∠4 = 360°

प्रश्न 3.
चतुर्भुज ABCD पर विचार कीजिए (आकृति के अनुसार)।माना इसके अभ्यंतर में कोई बिन्दु P स्थित है।

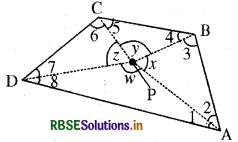
P को शीर्षों A, B, C तथा D से जोडिए।आकृति में, ΔPAB पर विचार कीजिए।हम देखते हैं कि x = 180° - m∠2m∠3; इसी प्रकार APBC, से y = 180° - m∠4 - m∠5, ΔPCD से z = 180° - m∠6 - m∠7 और ΔPDA, w = 180° - m∠8 - m∠1 इसका उपयोग करके कुल माप m∠1 + m∠2 + ... + m∠8, ज्ञात कीजिए। क्या यह आप को परिणाम तक पहुंचाने में सहायता करता है? याद रखिए, 2x + ∠y + 2 + ∠w = 360° है।
हल:
हम जानते हैं कि किसी त्रिभुज के तीनों कोणों का योग 180° होता है।
अतः x = 180° - ∠2 - ∠3 .....(1)
y = 180° - ∠4 - ∠5 .....(2)
z = 180° - ∠6 - ∠7 .....(3) और
w = 180° - ∠8 - ∠1 .....(4)

(1), (2), (3) तथा (4) को जोड़ने पर, 
x + y + z + w = 720° – (∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8)
परन्तु x + y + z + w = 360°
360° = 720° - (∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8) 
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8
= 720° - 360° = 360°
इससे हम यह निष्कर्ष निकाल सकते हैं कि किसी चतुर्भुज के चारों कोणों का योग 360° होता है। 

प्रश्न 4.
ये सभी चतुर्भुज उत्तल (Convex) चतुर्भुज थे। यदि चतुर्भज उत्तल नहीं होते तो क्या होता? चतुर्भुज ABCD पर विचार. कीजिए। इसे दो त्रिभुजों में बाँटिए और अंतःकोणों का योगफल ज्ञात कीजिए। (आकृति देखें।

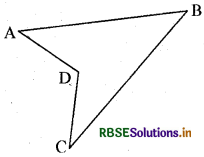
हल:
चतु भुज ABCD में BD को Aरा मिलाया, जैसा कि आकृति में दिखाया गया है। कोणों को चिह्नित कर नाम दिया। त्रिभुज के तीनों कोणों के योग गुणधर्म का प्रयोग करने पर

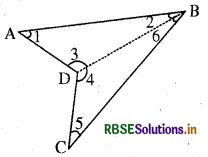
(m∠1 + m∠2 + m∠3) + (m∠4+ m∠5 + m∠6) = 180° + 180°
⇒ m∠1 + (m∠2 + m∠6) + m∠5 + (m∠3 + m∠4) =360°
⇒ m∠A + m∠B + m∠C + m∠D = 360°
अतः अंत:कोणों का योग 360° है।

(प्रयास कीजिए - पृष्ठ 47)

प्रश्न 1.
एक सम षड्भुज लीजिए (आकृति के अनुसार)

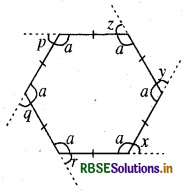
1. बाह्य कोणोंx,y, ,p, q तथा r की मापों का योग क्या है?
2. क्या x = y = z = p = q = r है? क्यों?
3. प्रत्येक की माप क्या है?
(i) बाह्य कोण
(ii) अन्तःकोण
4. इस क्रियाकलाप को निम्नलिखित के लिए दोहराएँ
(i) एक सम अष्टभुज
(ii) एक सम 20 भुज
हल:
1. माना कि सम षड्भुज की भुजाओं को क्रम से बढ़ाया जाता है जैसा कि आकृति में दिखाया गया है। इस प्रकार कोण x, y, z, p, q तथा r बाह्य कोण बनते हैं। क्योंकि बाह्य कोण x तथा अन्त:कोण a रैखिक युग्म बनाता है और रैखिक युग्म के कोणों का योग 180° होता है।
∴ x + ∠a = 180° 
इसी प्रकार, y + ∠a = 180°
z + ∠a = 180° 
p + ∠a = 180° 
q + ∠a= 180°
r + ∠a = 180°
दोनों पक्षों के कोणों को जोड़ने पर, (x + y + z + p + q + r) + (∠a + ∠a + ∠a + ∠a + ∠a + ∠a) = 1080°
⇒ (x + y + z + p + q+ r) + (6 - 2) x 180° = 1080°
∴ (x+ y + z + p + q+ r) + 720° = 1080°
= x + y + z + p + q + r = 1080° - 720°
= 360°
अतः बाह्य कोणों की मापों का योग 360° होता है।

2. हाँ, x = y = z = p = q = r; क्योंकि इनमें से प्रत्येक 180° - a के बराबर है।
3. सम षड्भुज के सन्दर्भ में
(i) प्रत्येक बाह्य कोण = 360° = 60° 
(ii) प्रत्येक अन्तःकोण
= \(\frac{(n-2) \times 180^{\circ}}{n}\), जहाँ n = 6
= \(\frac{(6-2) \times 180^{\circ}}{6}=\frac{4 \times 180^{\circ}}{6}\)
= 4 × 30° = 120°

4. (i) एक सम,अष्टभुज के सन्दर्भ में, n = 8 लेने पर 
प्रत्येक अंत:कोण = \(\frac{(8-2) \times 180^{\circ}}{8}\)
= \(\frac{6 \times 180^{\circ}}{8}\) =135°
और प्रत्येक बाह्य कोण = 180° -135° = 450 

(ii) एक सम 20 भुज के सन्दर्भ में, n = 20 लेने पर
प्रत्येक अंत:कोण = \(\frac{(20-2) \times 180^{\circ}}{20}\)
= 18 × 9° = 162° 
और प्रत्येक बाह्य कोण = 180° - 162° = 18° 

(इन्हें कीजिए - पृष्ठ 49)

प्रश्न 1.
समान सर्वांगसम त्रिभुजों के कटे हुए भाग लीजिए जिनकी भुजाएँ 3 cm, 4 cm, 5 cm हैं। इन्हें व्यवस्थित कीजिए जैसा कि आकृति में दर्शाया गया है-(आकृति के अनुसार)।

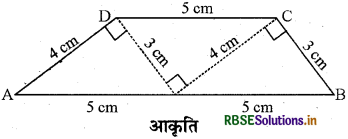
आकृति आपको एक समलम्ब प्राप्त होता है। (निरीक्षण कीजिए). यहाँ पर कौनसी भुजाएँ समान्तर हैं? क्या असमान्तर भुजाएँ बराबर माप की होनी चाहिए?

इन समान त्रिभुजों के समूह का उपयोग कर आप दो और समलम्ब प्राप्त कर सकते हैं। उनको ढूंढ़िए और उनकी आकृतियों की चर्चा कीजिए। हल- दी गई आकृति में,
AD = CE = 4 सेमी.
AE = DC = 5 सेमी.
क्योंकि चतुर्भुज AECD की सम्मुख भुजाएँ बराबर माप की हैं, इसलिए AECD एक समान्तर चतुर्भुज है।
∴ AE ∥ DC = AB ∥ DC 
∴ ABCD एक समलम्ब है जिसमें AB ∥ DC है तथा इसकी सम्मुख भुजाएँ AD और BC बराबर माप की नहीं
इन समान त्रिभुजों के समूह का उपयोग कर प्राप्त और सम्भव समलम्ब इस प्रकार हैं :

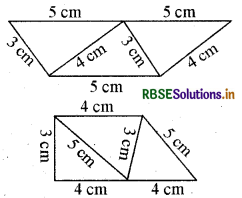
(इन्हें कीजिए - पृष्ठ 52)

प्रश्न 1.
दो समान समान्तर चतुर्भुजों के कटे हुए भाग ABCD तथा ABCD लीजिए (आकृति के अनुसार )।

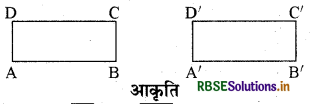
आकृति यहाँ पर भुजा \(\overline{{A B}}\) भुजा \(\overline{{A}^{\prime}{B}^{\prime}}\) के समान है परन्तु इनके नाम अलग-अलग हैं। इसी प्रकार, दूसरी संगत भुजाएँ भी समान हैं।
\(\overline{{A}^{\prime}{B}^{\prime}}\) को \(\overline{{D C}}\) के ऊपर रखिए। क्या वे एकदूसरे को पूर्णतया ढकती हैं?
हल:
हाँ, वे एक दूसरे को पूर्णतया ढकती हैं क्योंकि समान्तर चतुर्भुज ABCD तथा A'B'C'D' समान सर्वांगसम हैं तथा दोनों की सम्मुख भुजाएँ भी बराबर हैं।

प्रश्न 2.
अब आप \(\overline{{A B}}\) तथा \(\overline{{D C}}\) की लम्बाई के बारे में क्या कह सकते हैं?
हल:
समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं | अत: \(\overline{{A B}}\) और \(\overline{{D C}}\) बराबर लम्बाई की हैं।

प्रश्न 3.
इसी प्रकार \(\overline{{A D}}\) तथा \(\overline{{B C}}\) की लम्बाई की जाँच कीजिए। आप क्या पाते हैं?
हल:
\(\overline{{A D}}\) और \(\overline{{B C}}\) बराबर माप की हैं। हम \(\overline{{A B}}\) तथा \(\overline{{D C}}\) को माप कर इस परिणाम पर पहुँच सकते हैं।

(प्रयास कीजिए - पृष्ठ 52)

प्रश्न 1.
30° - 60° - 90° कोणों वाले दो समान सेटस्क्वेयर लीजिए। अब इन्हें आपस में इस प्रकार मिलाकर रखिए जिससे एक समान्तर चतुर्भुज बन जाए ( आकृति के अनुसार )। क्या यह ऊपर बताए गए गुण की पुष्टि करने में आपकी सहायता करता है?

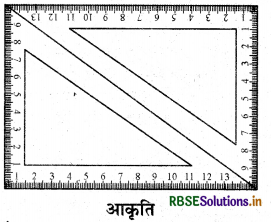
हल:
हाँ, बनाये गये समान्तर चतुर्भुज में सम्मुख भुजाएँ बराबर लम्बाई की हैं।

(इन्हें कीजिए - पृष्ठ 53)

प्रश्न 1.
माना ABCD एक समान्तर चतुर्भुज है ( आकृति के अनुसार) ट्रेसिंग शीट पर इसकी प्रतिलिपि बनाइए। इस प्रतिलिपि को A'B'C'D' से प्रदर्शित कीजिए। A'B'C'D' को ABCD पर आच्छादित कीजिए। दोनों चतुर्भुजों को आपस में मिलाकर उस बिन्दु पर पिन लगाइए जहाँ पर उनके विकर्ण प्रतिच्छेद करते हों, ट्रेसिंग शीट को 180° घुमाइए। समान्तर D चतुर्भुज अभी भी एक दूसरे को । पूर्णतया ढक लेते हैं; परन्तु अब आप देखते हैं कि A पूर्ण रूप से C पर और C पूर्ण रूप से B' पर आ जाता है। इसी प्रकार B' बिन्दु D

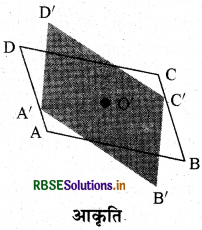
पर जाता है और विलोम रूप से भी सत्य है। क्या यह कोण A तथा कोण C के मापों के बारे में आपको कुछ बताता है? कोण B तथा D के मापों के लिए जाँच कीजिए। अपने निष्कर्ष की चर्चा कीजिए। हल-इसके द्वारा हम देखते हैं कि ∠A = ∠C तथा ∠B = ∠D है। अतः समान्तर चतुर्भुज के सम्मुख कोण. बराबर माप के होते हैं।

(प्रयास कीजिए - पृष्ठ 53)

प्रश्न 1.
30° - 60° - 90° कोणों वाले दो समान सेटस्क्वे यर लेकर पहले की तरह ही एक समान्तर चतुर्भुज बनाइए। क्या प्राप्त आकृति ऊपर बताए गए गुण की पुष्टि करने में आपकी सहायता करती है? 
हल:
हाँ ! प्राप्त आकृति ऊपर बताए गए गुण की पुष्टि करने में सहायता करती है कि समान्तर चतुर्भुज सम्मुख कोण बराबर माप के होते हैं।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 54)

प्रश्न 1.
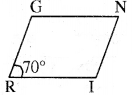
m∠R = m∠N = 70°, दर्शाने के उपरान्त क्या आप किसी अन्य विधि से m और m∠G को ज्ञात कर सकते हैं?
हल:
यह दिया गया है कि एक समान्तर चतुर्भुज RING में, m∠R = 70° चूँकि RG ∥ IN और RI एक प्रतिच्छेदक है जो इनको क्रमशः R और I पर प्रतिच्छेदित करता है इसलिए
∠R + ∠I = 180° 
[अंतःसम्मुख कोण] 
⇒ 70° + ∠I = 180°
⇒ ZI = 180° - 70° 
= 110°

पुनः RI ∥ GN तथा RG प्रतिच्छेदक है जो इनको क्रमश: R और G पर प्रतिच्छेदित करता है, इसलिए
∠R + ∠G = 180° [अंतःसम्मुख कोण] 
70° + ∠G = 180°
∠G = 180° - 70° = 110° 
अतः ∠I = ∠G = 110°

(इन्हें कीजिए - पृष्ठ 55)

प्रश्न 1.
समान्तर चतुर्भुज, (मान लीजिए ABCD) का एक कटा हुआ भाग लीजिए (देखें आकृति)। माना इसके विकर्ण \(\overline{{A C}}\) तथा DB एक-दूसरे को 'O' पर प्रतिच्छेद करते हैं।

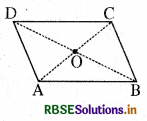
C को A पर रखकर एक तह (Fold) के द्वारा \(\overline{{A C}}\) का मध्य बिन्दु ज्ञात कीजिए।क्या मध्य बिन्दु O ही है? क्या यह दर्शाता है कि विकर्ण DB. विकर्ण \(\overline{{A C}}\) को बिन्द 'O' पर समद्विभाजित करता है? अपने मित्रों के साथ इसकी चर्चा कीजिए। इस क्रियाकलाप को यह ज्ञात करने के लिए दोहराएँ कि DB का मध्य बिन्दु कहाँ पर स्थित होगा?
हल:
एक बार मोड़कर \(\overline{{A C}}\) का मध्य बिन्दु ज्ञात करने तथा C को A पर रखने पर हम पाते हैं कि मध्य बिन्दु, बिन्दु O है जो विकर्ण \(\overline{{A C}}\) तथा BD का प्रतिच्छेदक बिन्दु है। अतः समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।

(पृष्ठ 60 - इन्हें कीजिए)

प्रश्न 1.
एक वर्गाकार शीट, माना PQRS लीजिए (आकृति के अनुसार)।

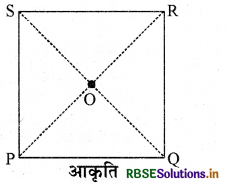
आकृति दोनों विकर्णों के अनुदिश तह (fold) लगाइए। क्या उनके मध्य बिन्दु समान ही हैं। सेट-स्क्वेयर का उपयोग करके जाँच कीजिए, क्या '0' पर बना कोण 90° का है। यह ऊपर बताए गए गुणधर्म को सिद्ध करता है।
हल:
(i) हाँ, दोनों विकर्णों के मध्य बिन्दु समान हैं।
(ii) हाँ, 'O' पर बना कोण 90° का है। अतः वर्ग के विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते हैं । तर्क-वितर्क की सहायता से भी हम इसकी पुष्टि कर सकते हैं।
∴ ABCD एक वर्ग है जिसके विकर्ण एक दूसरे को 'O' पर प्रतिच्छेद करते हैं। 
ΔAOD व ΔCOD में, 
OA = OC (... वर्ग एक समान्तर चतुर्भुज है।) SSS सर्वांगसमता प्रतिबन्ध के अनुसार ।
ΔAOD ≅ ΔCOD
अतः m∠AOD = m∠COD
और, m∠AOD + m∠COD = 180 ° (रैखिक युग्म)
2m∠AOD = 180° m∠AOD = 90°
∴ वर्ग के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 61)

प्रश्न 1.
एक राजमिस्त्री एक पत्थर की पट्टी बनाता है। वह इसे आयताकार बनाना चाहता है। कितने अलगअलग तरीकों से उसे यह विश्वास हो सकता है कि यह आयताकार है?
हल:
राजमिस्त्री को निम्नलिखित अलग-अलग तरीकों से यह विश्वास हो सकता है कि उसने जो पत्थर की पट्टी बनाई है वह आयताकार है
(i) यदि इसकी सम्मुख भुजाएँ बराबर हों।
(ii) यदि इसके विकर्ण बराबर हों।
(iii) यदि इसका प्रत्येक कोण 90° का हो।

प्रश्न 2.
वर्गको आयत के रूप में परिभाषित किया गया था जिसकी सभी भुजाएँ बराबर होती हैं। क्या हम इसे सम चतुर्भुज के रूप में परिभाषित कर सकते हैं जिसके कोण बराबर माप के हों? इस विचार को स्पष्ट कीजिए।
हल:
हाँ, हम सम चतुर्भुज के रूप में वर्ग को परिभाषित कर सकते हैं। एक सम चतुर्भुज जिसके कोण बराबर माप के हों, वर्ग है क्योंकि कोण बराबर माप के होते ही प्रत्येक कोण \(\frac{360^{\circ}}{4}\) = 90° का हो जाता है। इस प्रकार सभी भुजाएँ बराबर लम्बाई की तथा सभी कोण 90° माप की हो जाती हैं। इसलिए यह एक वर्ग है। 

प्रश्न 3.
क्या एक समलम्ब के सभी कोण बराबर माप के हो सकते हैं? क्या इसकी सभी भुजाएँ बराबर हो सकती हैं? वर्णन कीजिए।
हल:
हाँ, जब समलम्ब के सभी कोण बराबर माप के हो जाते हैं, तब वह या तो आयत होता है या वर्ग होता है। हाँ, जब समलम्ब की सभी भुजाएँ बराबर हो जाती हैं तब वह या तो सम चतुर्भुज होता है या वर्ग होता है।