RBSE Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 3 Understanding Quadrilaterals Roots Intext Questions

(Page No: 37)

Question 1.
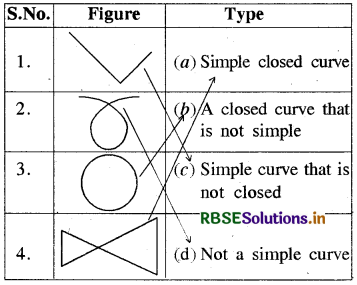
Match the following

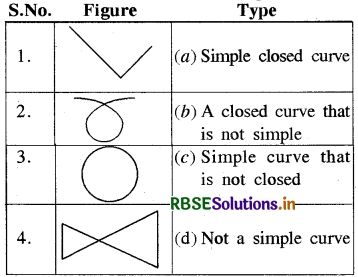
Answer:
It is matched as below:

(Do This Page No: 40)

Question 1.
Take any quadrilateral, say ABCD. Divide it into two triangles, p by drawing a diagonal. You get six angles 1, 2, 3, 4, 5 and 6.

Use the angle-sum property of a triangle and argue how the sum of the measures of ∠A, ∠B, ∠C and ∠D amounts to 180° + 180° = 360°.
Answer:
Let ABCD be a quadrilateral. Here AC is a diagonal.
∴ ∠1 + ∠4 = ∠A
and ∠2 + ∠5 = ∠C
We know that the sum of the angles of a triangle is 180°. Therefore,
In ∆ABC ∠4 + ∠5 + ∠B = 180° ............ (1)
and, In ∆ACD
∠1 + ∠2 + ∠D = 180° .......... (2)
Adding (1) and (2), we get
(∠4 + ∠5 + ∠B) + (∠1 + ∠2 + ∠D) = 180° + 180°
⇒ (∠1 + ∠4) + ∠B + (∠2 + ∠5) +∠D = 360°
⇒ ∠A + ∠B + ∠C + ∠D = 360°
[∵ ∠1 + ∠4 = ∠A and ∠2 + ∠5 = ∠C]
Hence, the sum of the angles of a quadrilateral is 360°.

Question 2.
Take four congruent card-board copies of any quadrilateral ABCD, with angles as shown [Fig (i)]. Arrange the copies as shown in the figure, where angles ∠1, ∠2, ∠3, ∠4 meet at a point [Fig (ii)].

What can you say about the sum of the angles ∠1, ∠2, ∠3 and ∠4?
Answer:
We know that the sum of the angles of a quadrilateral is 360°. In quadrilateral ABCD,
∠A + ∠B + ∠C + ∠D = 360°
∴ m∠1 + m∠2 + m∠3 + m∠4 = 360°

Question 3.
As before consider quadrilateral ABCD. Let P be any point in its interior. Join P to vertices A, B, C and D. In the figure,

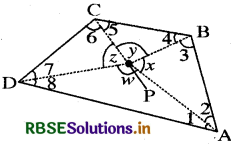
consider APAB. From this we see x = 180° - m∠2 - m∠3; similarly from ∆PBC, y = 180° - m∠4 - m∠5, from ∆PCD, z = 180° - m∠6 - m∠7 and from ∆PDA, w = 180° - m∠8 - m∠1. Use this to find the total measure m∠1 + m∠2 + ... + m∠8, does it help you to arrive at the result? Remember ∠x + ∠y + ∠z + ∠w = 360°.
Answer:
We know that the sum of the angles of a triangle is 180°.
∴ x = 180° - ∠2 - ∠3 ....... (1)
y = 180° - ∠4 - ∠5 ..... (2)
z = 180° - ∠6 - ∠7 ...... (3)
and w = 180° - ∠8 - ∠1 ...... (4)
Adding (1), (2), (3) and (4) we get,
x + y + z + w = 720° - (∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8)
But x + y + z + w= 360°
∴ 360° = 720° - (∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8)
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 720° - 360° = 360°
This help us to arrive at the result that the sum of the angles of a quadrilateral is 360°.

Question 4.
These quadrilaterals were con-vex. What would happen if the quadrilateral is not convex? Consider quadrilateral ABCD. Split it into two triangles and find the sum of the interior angles (see figure).

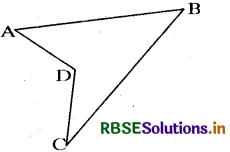
Answer:
In the quadrilateral ABCD, we join BD. We mark the angles as shown in the figure. Using the angle sum property of a triangle, we have
(m∠1 + m∠2 + m∠3) + (m∠4 + m∠5 + m∠6)
= 180°+ 180°

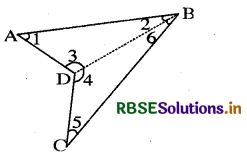
⇒ m∠1 + (m∠2 + m∠6) + m∠5 + (m∠3 + m∠4)
⇒ 360°
⇒ m∠A + m∠B + m∠C + m∠D = 360°
Hence, die sum of its interior angles is 360°.

(Do This Page No: 43)

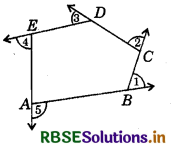
Question 1.
Draw a polygon on the floor, using a piece of chalk. (In the figure, a pentagon ABCDE is shown)
Answer:
We want to know the total measure of angles, i.e. m∠1 + m∠2 + m∠3 + m∠4 + m∠5. Start at A, walk along \(\overline{A B}\). On reaching B, you need to turn through an angle of m∠1, to walk along \(\overline{B C}\). When you reach at C, you need to turn through an angle of m∠2 to walk along \(\overline{C D}\). You continue to move in this manner, until you return to side \(\overline{B C}\). You would have in fact made one complete turn. Therefore, m∠1 + m∠2 + m∠3 + m∠4 + m∠5 = 360°. This is true whatever be die number of sides of the polygon Therefore, the sum of the measures of the exterior angles of any polygon is 360°.

(Try These Page No: 43)

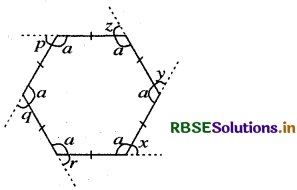
Take a regular hexagon (see figure).
1. What is the sum of the measures of its exterior angles x, y, z, p, q, r?
2. IS x = y = z = p = q = r? Why?
3. What is the measure of each?
(i) exterior angle
(ii) interior angle
4. Repeat this activity for the cases of
(i) a regular octagon
(ii) a regular 20-gon
Answer:
1. Let the sides of a regular hexagon ABCDEF be produced in order as shown in the figure, forming exterior angles x, y, z, p, q and r.
Since the exterior angle ∠x and the interior angle ∠a form a linear pair and we know that the sum of the angles of a linear pair is 180°.
∴ x + ∠a = 180°
Similarly, y + ∠a = 180°
z + ∠a = 180°
p + ∠a = 180°
q + ∠a = 180°
r + ∠a = 180°
Adding the angles of both sides, we get
(x + y + z + p + q + r) + (∠a + ∠a + ∠a + ∠a + ∠a + ∠a) = 1080°
⇒ (x + y + z + p + q + r) + ( 6 - 2) × 180° = 1080°
∴ (x + y + z + p + q + r) + 720° = 1080°
⇒ x + y + z + p + q + r= 1080° - 720°
= 360°
Hence, the sum of the measures of its exterior angles is 360°.

2. Yes, x = y = z = p = q = r, because each of them is equal to 180° - a

3. In case of regular hexagon—
(i) each exterior angle = \(\frac{360^{\circ}}{6}\) = 60°
(ii) each interior angle
= \(\frac{(n-2) \times 180^{\circ}}{n},\) where n = 6
= \(\frac{(6-2) \times 180^{\circ}}{6}\) = \(\frac{4 \times 180^{\circ}}{6}\)
= 4 × 30° = 120°

4. (i) In case of regular octagon, we take n = 8, then each interior angle = \(\frac{(8-2) \times 180^{\circ}}{8}\) = \(\frac{6 \times 180^{\circ}}{8}\) = 135° and, each exterior angle = 180° - 135° = 45°
(ii) In case of regular 20-gon. We take n = 20, then each intenor angle = \(\frac{(20-2) \times 180^{\circ}}{20} \)= 18 × 9 = 162°
and, each exterior angle = 180° - 162° = 18°

(Do This Page No: 44)

Question 1.
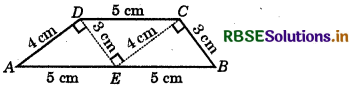
Take identical cut-outs of congruent triangles of sides 3 cm, 4 cm, 5 cm. Arrange them as shown in figure. You get a trapezium. (Check it!) Which are the parallel sides here? Should the non-parallel sides be equal? You can get two more trapeziums using the same set of triangles. Find them out and discuss their shapes.

Answer:
∵ In the given figure,
AD = CE = 4 cm
AE = DC = 5 cm
As the opposite sides of quadrilateral
AECD are equal, therefore, AECD is a parallelogram.
∵ AE || DC ⇒ AB || DC
∴ ABCD is a trapezium with AB || DC, also its opposite sides AD and BC are not equal.
More possible trapeziums using the same set of triangles are as follows:

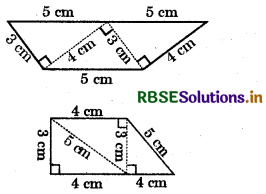
Question 2.
Take four set-squares from your and your friend’s instrument boxes. Use different numbers of them to place side-by-side and obtain different trapeziums. If the non-parallel sides of a trapezium are of equal length, we call it an isosceles trapezium. Did you get an isosceles trapezium in any of your investigations given above?
Answer:
By taking the different number of set-squares and placing them side-by-side, we obtain the following trapeziums:

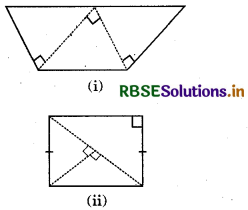
Yes, we get an isosceles trapezium in investigation.

(Do This Page No: 45)

Question 1.
Take a thick white sheet. Fold the paper once. Draw two line segments of different lengths as shown in figure. Cut along the line segments and open up. You have the shape of a kite. Has the kite any line symmetry?

Fold both the diagonals of the kite. Use the set-square to check if they cut at fight angles. Are the diagonals equal in length? Verify (by paper-folding or measurement) if the diagonals bisect each other. By folding an angle of the kite on its opposite, check for angles of equal measure.
Observe the diagonal folds; do they indicate any diagonal being an angle bisector? Share your findings with others and list them. A summary of these results are given elsewhere in the chapter for your reference.
Answer:

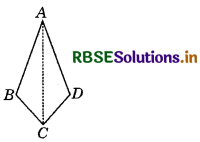
(i) The kite has one line of symmetry and it is diagonal AC, because diagonal AC divides ∠A and ∠C into two equal parts and ∠B = ∠D.
Yes, the diagonals cut at right angles.
(ii) The diagonals are not equal.
(iii) No, the diagonals do not bisect each other.

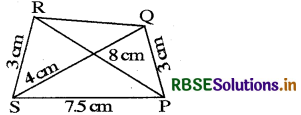
Question 2.
Show that ∆ABC and ∆ADC are congruent. What do we infer from this?
Answer:

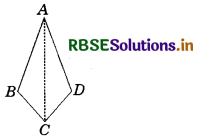
In ∆ABC and ∆ADC, we have
AB = AD
(One pair of consecutive sides)
BC = DC
(One pair of consecutive sides)
Also, AC = AC B<
(Common sides)
∴ By SSS congruence criterion
∆ABC ≅ ∆ADC
∴ ∠BAC = ∠DAC and ∠BCA = ∠DCA [By CPCT]
i.e. diagonal AC bisects ∠A and ∠C each.

(Do This Page No: 46)

Question 1.
Take two different rectangular cardboard strips of different widths:

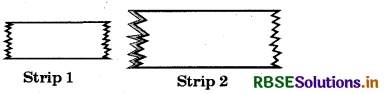
Place one strip horizontally and draw lines along its edge as drawn in the fig. (i).

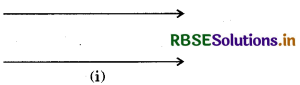
Now place the other strip in a slant position over the lines drawn and use this to draw two more lines as shown in fig. (ii).
These four lines enclose a quadrilateral. This is made up of two pairs of parallel lines [Fig. (iii)].

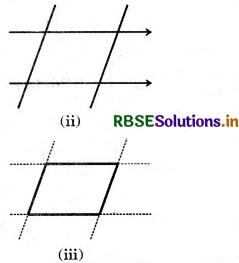
(Try These Page No: 47)

Take cut-outs of two identical parallelograms, say ABCD and A'B'C'D'.

Here, \(\overline{A B}\) is same as \(\overline{A^{\prime} B^{\prime}}\) except for the name. Similarly, the other corresponding sides are equal too.

Question 1.
Place \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\) over \(\overline{D C}\). Do they coincide?
Answer:
Yes, they will coincide as the parallelograms ABCD and A'B'C’D' are identical, also opposite sides of parallelogram are equal.

Question 2.
What can you now say about the lengths \(\overline{A B}\) and \(\overline{D C}\) ?
Answer:
Opposite sides of parallelogram are equal, so \(\overline{A B}\) and \(\overline{D C}\) are equal in length.

Question 3.
Similarly, examine the lengths \(\overline{A D}\) and \(\overline{B C}\). What do you find?
Answer:
\(\overline{A D}\) and \(\overline{B C}\) are equal.
We may also arrive at this result by measuring \(\overline{A D}\) and \(\overline{B C}\).

(Try These Page No: 47)

Question 1.
Take two identical set squares with angles 30° - 60° - 90° and place them adjacently to form a parallelogram as shown in fig. Does this help you to verify the above property?
Answer:
Yes, opposite sides of the formed parallelogram are equal.

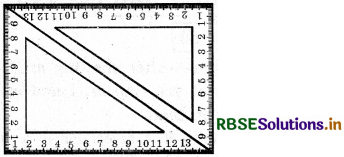
(Do This Page No: 48)

Question 1.
Let ABCD be a parallelogram as shown in fig. Copy it on a tracing sheet. Name this copy as A'B'C'D'. Place A'B'C'D' on ABCD. Pin them together at the point where the diagonals meet. Rotate the transparent sheet by 180°. The parallelograms still genocide; but you now find A' lying exactly on C and vice-versa; similarly B' lies on D and vice-versa.
Does this tell you anything about the measures of the angles A and C? Examine the same for angle B and D. State your findings.
Solution :
By this, we find that ∠A = ∠C and ∠B = ∠D. Therefore, the opposite angles of a parallelogram are of equal measure.

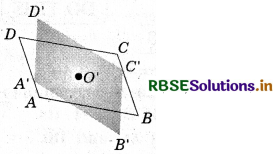
(Try These Page No: 48)

Question 1.
Take two identical 30°, 60°, 90° set- squares and form a parallelogram as before. Does the figure obtained help you to confirm the above property?
Answer:
Yes! The figure obtained helps to confirm the above property that opposite angles of a parallelogram are of equal measure.

(Think, Discuss and Write Page No: 50)

Question 1.
After showing m∠R = m∠N = 70°, can you find m∠I and m∠G by any other method?
Answer:

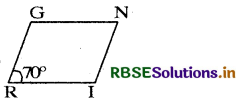
It is given that in a parallelogram RING, m∠R = 70°
Since RG || IN and RI is a transversal intersecting them at R and I respectively, therefore,
∠R + ∠I = 180°
(consecutive interior angles)
⇒ 70° + ∠I = 180°
⇒ ∠I = 180° - 70°
= 110°
Again RI || GN and RG is a transversal intersecting them at R and G respectively, therefore,
∠R + ∠G = 180° .
(consecutive interior angles)
⇒ 70° + ∠G = 180°
⇒ ∠G = 180° - 70° = 110°
Hence, ∠I = ∠G = 110°

(Do This Page No: 50)

Question 1.
Take a cut-out of a parallelogram, say, ABCD. Let its diagonals. \(\overline{\mathbf{A C}}\) and \(\overline{\mathbf{D B}}\) meet at O.

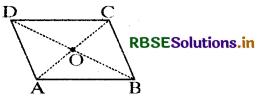
Find the mid point of by a \(\overline{\mathbf{A C}}\) fold, placing C on A. Is the midpoint same as O?
Does this show that diagonal \(\overline{\mathbf{D B}}\) bisects the diagonal \(\overline{\mathbf{A C}}\) at the point O? Discuss it with your friends. Repeat the activity to find where the mid point of \(\overline{\mathbf{D B}}\) could lie.
Answer:
On finding the mid-point of \(\overline{\mathbf{A C}}\) by a fold, placing C on A, we find that it is point O, the intersecting point of diagonals AC and BD. Hence, the diagonals of a parallelogram bisect each other.

(Do This Page No: 55)

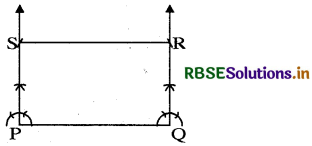
Question 1.
Take a square sheet, say PQRS. Fold along both the diagonals. Are their mid-points the same?
Check if the angle at O is 90° by using a set-square. This verifies the property stated above.

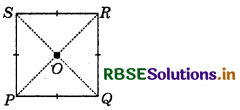
Answer:
(i) Yes, the mid-point of the diagonals are same.
(ii) Yes, the angle at O is 90°.
Hence, the diagonals of square are perpendicular bisector of each other. We can justify this also by arguing logically.
∵ ABCD is a square, whose diagonals meet at point ().
In ∆ AOD and ∆ COD,
OA = OC
(∵ OA = OC square is a parallelogram.)
AD = BC
(∵ All sides of square are equal.)
OD = OD (Common)
By SSS criteria,
∆ AOD = ∆ COD
Therefore, m∠AOD = m∠COD
Also m∠AOD + m∠COD = 180° (Linear pair)
⇒ 2 m∠AOD = 180°
⇒ m∠AOD = 90°
∴ Diagonals of square bisect each other at right angle.

(Think, Discuss And Write Page No: 56)

Question 1.
A mason has made a concrete slab. He needs it to be rectangular. In what different ways can he make sure that it is rectangular?
Answer:
To make a concrete rectangular slab the manson should ensure:

• its opposite sides equal;
• its diagonals equal;
• each angle measure 90°.

Question 2.
A square was defined as a rectangle with all sides equal. Can we define it as rhombus with equal angles? Explore this idea.
Answer:
Square can not be defined as a rhombus with equal angles as its diagonal will not be equal unless its each angle is 90°.

Question 3.
Can a trapezium have ail angles equal? Can it have all sides equal? Explain.
Answer:
A trapezium cannot have all angles equal as its opposite sides become parallel. But trapezium is a quadrilateral with one pair of parallel sides.
A trapezium cannot have all sides equal as again its opposite sides become parallel. But trapezium is a quadrilateral With one pair of parallel sides.