RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Ex 3.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Ex 3.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 3 चतुर्भुजों को समझना Ex 3.2

Class 8 Maths Chapter 3 Exercise 3.2 Solutions In Hindi Medium प्रश्न 1.
निम्नलिखित आकृतियों में x का मान ज्ञात कीजिए-

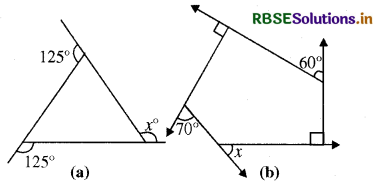
हल:
हम जानते हैं कि उत्तल बहुभुज की भुजाओं को क्रम में एक ओर बढ़ाने पर प्राप्त बाह्य कोणों का योग 360° होता है। इसलिए,
(a) x + 125° + 125° = 360°
या x + 250° = 360°
या x = 360° - 250°
= 110°

(b) x + 90° + 60° + 90° + 70° = 360°
या x + 310° = 360°
या x = 360° - 310°
= 50°

Class 8 Maths Chapter 3 Exercise 3.2 Solutions In Hindi प्रश्न 2.
एक सम बहुभुज के प्रत्येक बाह्य कोण की माप ज्ञात कीजिए जिसकी
(i) 9 भुजाएँ
(ii) 15 भुजाएँ हों।
हल:
(i)9 भुजाओं वाले सम बहुभुज का प्रत्येक बाह्य कोण
= \(\frac{360^{\circ}}{n}\), जहाँ n = 9
= \(\left(\frac{360}{9}\right)^{\circ}\) = 40° उत्तर

(ii) 15 भुजाओं वाले सम बहुभुज का प्रत्येक बाह्य कोण
= \(\frac{360^{\circ}}{n}\) जहाँ n = 15
= \(\left(\frac{360}{9}\right)^{\circ}\) = 24°

Class 8 Maths Chapter 3 Exercise 3.2 Hindi Medium प्रश्न 3.
एक सम बहुभुज की कितनी भुजाएँ होंगी यदि एक बाह्य कोण की माप 24° हो?
हल:
हम जानते हैं कि एक सम बहुभुज की भुजाओं की संख्या

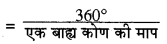
यहाँ एक बाह्य कोण की माप = 24°
अतः दिए गए बहुभुज की भुजाओं की संख्या
= \(\frac{360^{\circ}}{24^{\circ}}\) = 15

Class 8 Maths Chapter 3.2 Hindi Medium प्रश्न 4.
एक सम बहुभुज की भुजाओं की संख्या ज्ञात कीजिए यदि इसका प्रत्येक अंतःकोण 165° का हो?
हल:
माना कि इस बहुभुज की n भुजाएँ हैं। तब, इसका
प्रत्येक अंत:कोण = \(\left[\frac{(n-2) \times 180}{n}\right]\)
अतः \(\frac{n-2}{n}\) × 180 = 165
या 180n - 360 = 165n .
(दोनों पक्षों को n से गुणा करने पर)
या 180n - 165n = 360
या 15n = 360
या n = \(\frac{360}{15}\) = 24
अर्थात् इस बहुभुज की 24 भुजाएँ हैं।

3.2 Class 8 In Hindi प्रश्न 5.
(a) क्या ऐसा सम बहुभुज संभव है जिसके प्रत्येक बाह्य कोण की माप 22° हो?
(b) क्या यह किसी सम बहुभुज का अंतःकोण हो सकता है? क्यों?
हल:
(a) सम बहुभुज के भुजाओं की संख्या

∴ इस सम बहुभुज की भुजाओं की संख्या = \(\frac{360^{\circ}}{22^{\circ}}\)
[∵ बाह्य कोण की माप = 22°, दिया है]
= \(\left(\frac{180}{11}\right)^{\circ}\) = एक अपूर्णांक
चूँकि यह एक पूर्ण संख्या नहीं है। अतः 22° माप का बाह्य कोण वाला कोई सम बहुभुज संभव नहीं है।

(b) यदि अंत:कोण = 22°, तब इसका बाह्य कोण
= 180° - 22° = 158°
चूँकि 158° से 360° पूर्णतः विभाज्य नहीं है। अतः यह बहुभुज संभव नहीं है।

Ex 3.2 Class 8 Hindi Medium प्रश्न 6.
(a) किसी सम बहुभुज में कम से कम कितने अंश का अंतःकोण संभव है? क्यों?
हल:
समबाहु त्रिभुज तीन भुजाओं का एक सम बहुभुज है जिसका कम से कम अंत:कोण 60° का ही संभव है।

(b) किसी सम बहुभुज में अधिक से अधिक कितने अंश का बाह्य कोण संभव है?
हल:
क्योंकि एक सम बहुभुज के एक अंत:कोण का न्यूनतम माप 60° होता है, इस लिए अधिक से अधिक एक बाह्य कोण का सम्भव माप 18° - 60° = 120° है।