RBSE Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 3 Understanding Quadrilaterals Ex 3.2

Question 1.
Find x in the following figures

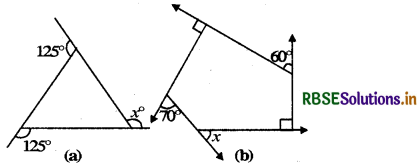
Answer:
We know that the sum of the exterior angles formed by producing the sides of a convex polygon in the same order is 360°. Therefore,
(a) x + 125° + 125° = 360°
or x + 250° = 360°
or x = 360° - 250°
= 110°
(b) x + 90° +. 60° + 90° + 70° = 360°
or x + 310° = 360°
or x = 360° - 310°
= 50°

Question 2.
Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Answer:
(i) Each exterior angle of a regular polygon of 9 sides
= \(\frac{360^{\circ}}{n}\), where n = 9
= \(\left(\frac{360}{9}\right)^{\circ}\) = 40°

(ii) Each exterior angle of a regular polygon of 15 sides
= \(\frac{360^{\circ}}{n}\), where n = 15
= \(\left(\frac{360}{15}\right)^{\circ}\) = 24°

Question 3.
How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Answer:
We know that the number of sides of a regular polygon
= \(\frac{360^{\circ}}{\text { Measure of a exterior angle }}\)
Here, exterior angle = 24°
∴ Number of sides of the give polygon
= \(\frac{360^{\circ}}{24^{\circ}}\) = 15

Question 4.
How many sides does a regular polygon have if each of its interior angles is 165°?
Answer:
Let the number of sides of the polygon be n. Then, its each interior angle
= \(\left[\frac{(n-2) \times 180}{n}\right]\)
∴ \(\frac{n-2}{n}\) × 180 = 165
or 180n - 360= 165n
(Multiplying both sides by n)
or 180n - 165n = 360
or 15n = 360
or n = \(\frac{360}{15}\) = 24
Hence, there are 24 sides of the polygon.

Question 5.
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
(b) Can it be an interior angle of a regular polygon? Why?
Answer:
(a) The number of sides of a regular polygon = \(\frac{360^{\circ}}{\text { Exterior angle }}\)
∴ The number of sides of a regular polygon = \(\frac{360}{22}\)
[∵ Exterior angle = 22°]
= \(\left(\frac{180}{11}\right)\)
which is not a whole number.
∴ It is not possible to have a regular polygon with measure of each exterior angle as 22°.

(b) If interior angle = 22°, then its exterior angle = 180° - 22° = 158°
But 158 does not divide 360 exactly.
Hence, the polygon is not possible.

Question 6.
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Answer:
(a) The equilateral triangle is a regular polygon of 3 sides which has the least measure of an interior angle = 60°
(b) Since the minimum interior angle of a regular polygon is 60°, therefore, the maximum exterior angle possible for a regular polygon = 180° - 60° = 120°.