RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Ex 3.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना Ex 3.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 3 चतुर्भुजों को समझना Ex 3.1

प्रश्न 1.
यहाँ पर कुछ आकृतियाँ दी गई हैं-

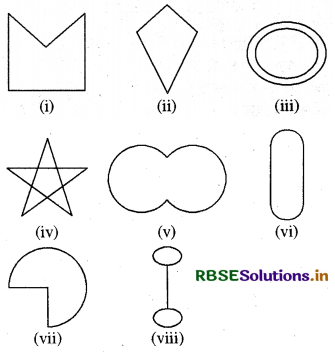
प्रत्येक का वर्गीकरण निम्नलिखित आधार पर कीजिए
(a) साधारण वक्र
(b) साधारण बंद वक्र
(c) बहुभुज
(d) उत्तल बहुभुज
(e) अवतल बहुभुज।
हल:
दी गई आकृतियों का वर्गीकरण निम्नानुसार है
(a) साधारण वक्र- (1), (2), (5), (6) और (7)
(b) साधारण बन्द वक्र- (1), (2), (5), (6) और (7)
(c) बहुभुज- (1), (2) और (4)
(d) उत्तल बहुभुज- (2)
(e) अवतल बहुभुज-(1) और (4)

प्रश्न 2.
निम्नलिखित प्रत्येक में कितने विकर्ण हैं?
(a) एक उत्तल चतुर्भुज
(b) एक सम षड्भुज
(c) एक त्रिभुज
हल:
(a) एक उत्तल चतुर्भुज में दो विकर्ण होते हैं।
(b) एक समषड्भुज में नौ विकर्ण होते हैं।
(c) एक त्रिभुज में कोई विकर्ण नहीं होता है।

प्रश्न 3.
उत्तल चतुर्भुज के कोणों की मापों का योगफल क्या है? यदि चतुर्भुज उत्तल न हो, तो क्या यह गुण लागू होगा? (एक चतुर्भुज बनाइए जो उत्तल न हो और प्रयास कीजिए।)
हल:
हम जानते हैं कि उत्तल चतुर्भुज के कोणों की मापों का योग 360° होता है। हाँ यदि चतुर्भुज उत्तल नहीं हो, तो भी यह गुण लागू होगा।

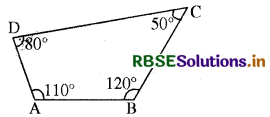
दिए गए चतुर्भुज ABCD में
= ∠A + ∠B + ∠C+ ∠D
= 110° + 120° + 50° + 80°
= 360°

प्रश्न 4.
तालिका की जाँच कीजिए-(प्रत्येक आकृति को त्रिभुजों में बाँटिए और कोणों का योगफल ज्ञात कीजिए।)

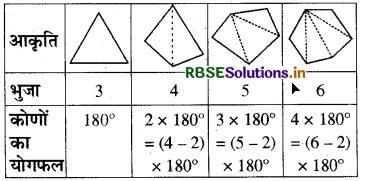
एक बहुभुज के कोणों के योग के बारे में आप क्या कह सकते हैं जिसकी भुजाओं की संख्या निम्नलिखित हो।
(a) 7
(b) 8
(c) 10
(d) n
हल:
दी गई तालिका से यह स्पष्ट होता है कि n भुजाओं वाले बहुभुज के कोणों (अन्तःकोणों) का योग
= (n - 2) × 180°

(a) यहाँ n = 7
∴ 7 भुजाओं वाले बहुभुज के कोणों का योग
= (7 - 2) × 180°
= 5 × 180° = 900°

(b) यहाँ n = 8
∴ 8 भुजाओं वाले बहुभुज के कोणों का योग
= (8 - 2) × 180°
= 6 × 180°
= 1080°

(c) यहाँ n = 10
∴ 10 भुजाओं वाले बहुभुज के कोणों का योग
= (10 - 2) × 180°
= 8 × 180°
= 1440°

(d) दी गई तालिका से स्पष्ट है कि बहुभुज में बने त्रिभुजों की संख्या उसकी भुजाओं की संख्या से दो कम है। अतः यदि बहुभुज में भुजाएँ n हैं तो उस बहुभुज में बने त्रिभुजों . की संख्या (n - 2) × 180° होगी।
एक त्रिभुज के तीनों कोणों का योग = 180°
∴ n भुजाओं बाले बहुभुज के कोणों का योग
= (n - 2) × 180°

प्रश्न 5.
सम बहुभुज क्या है? एक सम बहुभुज का नाम बताइए जिसमें
(i) 3 भुजाएँ
(ii) 4 भुजाएँ
(iii) 6 भुजाएँ हों।
हल:
एक बहुभुज को सम बहुभुज कहते हैं यदि इसके
(a) सभी अंत:कोण बराबर हों;
(b) भुजाएँ बराबर हों और
(c) बाह्य कोण बराबर हों।
सम बहुभुज जिनकी
(i) 3 भुजाएँ हैं, समबाहु त्रिभुज कहलाता है।
(ii) 4 भुजाएँ हैं, वर्ग कहलाता है।
(iii) 6 भुजाएँ हैं, सम षड्भुज कहलाता है।

प्रश्न 6.
निम्नलिखित आकृतियों में x (कोण की माप) ज्ञात कीजिए
(a)

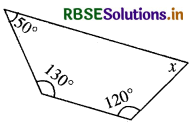
हल:
हम जानते हैं कि चतुर्भुज के चारों कोणों (अंतःकोणों) का योग 360° होता है।
अतः x + 120° + 130° + 50° = 360° .
या x + 300° = 360°
या x = 360° - 300°
= 60°

(b)

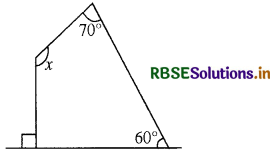
हल:
हम जानते हैं कि चतुर्भुज के चारों कोणों (अंत:कोणों) का योग 360° होता है।
अतः x + 70° + 60° + 90° = 360°
या x + 220° = 360°
या x = 360° - 220°
= 140°

(c)

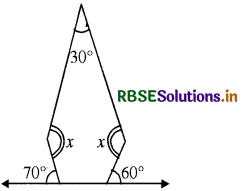
हल:

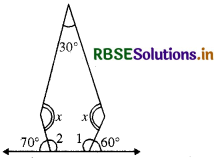
प्रश्नानुसार दी गई आकृति में 5 भुजाएँ हैं अर्थात् n = 5
∴ इस आकृति के सभी कोणों का योग
= (n - 2) × 180°
= (5 - 2) × 180°
= 3 × 180°
= 540°
आकृति से स्पष्ट है कि
m∠1 + 60° = 180° [रैखिक युग्म]
या m∠1 = 180° - 60° = 120°
और m∠2 + 70° = 180° [रैखिक युग्म]
या m∠2 = 180° - 70° = 110°
अतः m∠1 + m∠2 + x + 30° = 540°
या 120° + 110° + 2x + 30° = 540°
या 2x + 260° = 540°
या 2x = 540° - 260° = 280°
या x = \(\frac{280^{\circ}}{2}\) = 140°.

(d)

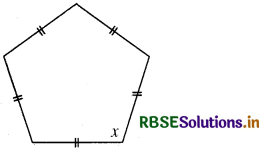
हल:
प्रश्नानुसार दी गई आकृति में 5 भुजाएँ हैं आर्थत्
n = 5
अतः इस आकृति में कोणों का योग
= (n - 2) × 180°
= (5 - 2) × 180°
= 3 × 180° = 540°
∴ x + x + x + x + x = 540°
या 5x = 540°
या x = \(\frac{540^{\circ}}{5}\)
= 108°

प्रश्न 7.

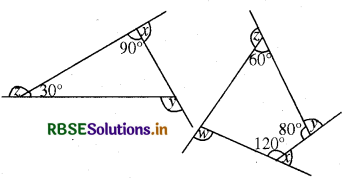
(a) x + y + z ज्ञात कीजिए।
(b) x + y + z + w ज्ञात कीजिए।
हल:
(a) हम जानते हैं कि एक त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।
∴ m∠1 + 30° + 90° = 180°
या m∠1 + 120° = 180°

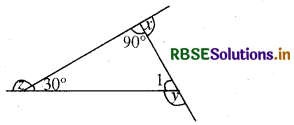
या m∠1 = 180° - 120° = 60°
और x + 90° = 180° [रैखिक युग्म]
या x = 180° - 90° = 90° ......... (1)
y + m∠1 = 180° [रैखिक युग्म]
या y + 60° = 180° [:: m21 = 60°]
या y = 180° - 60° = 120° ......... (2)
और z + 30° = 180° [रैखिक युग्म]
या z = 180° - 30° = 150° ............... (3)
(1), (2) और (3) को जोड़ने पर
x + y + z = 90° + 120° + 150°
= 360°

(b) हम जानते हैं कि चतुर्भुज के चारों कोणों का योग 360° होता है, अतः
m∠1 + 120° + 80° + 60° = 360°
या m∠1 + 260° = 360°
या m∠1 = 360° - 260° = 100°

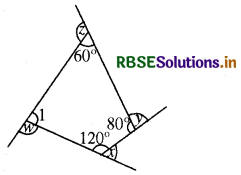
और x + 120° = 180° [रैखिक युग्म]
x = 180° - 120° = 60° ....... (1)
y + 80° = 180° रैखिक युग्म]
या y = 180° - 80°
= 100° ......... (2)
z + 60° = 180° [रैखिक युग्म]
या z = 180° - 60° = 120° .........(3)
और m∠1 + w = 180° [रैखिक युग्म]
या w = 180° - m∠1
= 180° - 100
= 80° ......... (4)
(1), (2), (3) और (4) को जोड़ने पर
x + y + z + w = 360°
60° + 100° + 120° + 80° = 360°