RBSE Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 3 Understanding Quadrilaterals Ex 3.1

Question 1.
Given here are some figures.

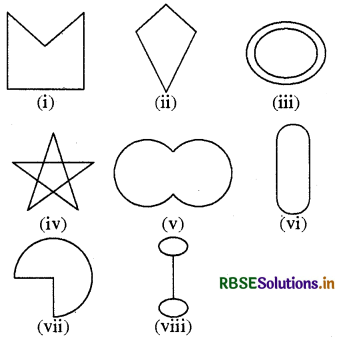
Classify each of them on the basis of the following.
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Answer:
The classification of the given figures is given below :
(a) Simple curve: (i), (ii), (v), (vi) and (vii)
(b) Simple closed curve: (i), (ii), (v), (vi) and (vii)
(c) Polygon: (i), (ii) and (iv)
(d) Convex Polygon: (ii)
(e) Concave Polygon: (i) and (iv)

Question 2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon (C) A triangle
Answer:
(a) A convex quadrilateral has two diagonals.
(b) A regular hexagon has nine diagonals.
(c) A triangle has no diagonal.

Question 3.
What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)
Answer:
We know that the sum of measures of the angles of a convex quadrilateral is 360°.
Yes, this property holds in case of the quadrilateral is not convex.

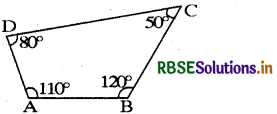
In given quadrilateral ABCD,
= ∠A + ∠B + ∠C + ∠D
= 110° + 120° + 50° + 80°
= 360°

Question 4.
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

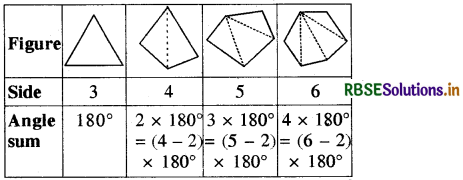
What can you say about the angle sum of a convex polygon with number of sides?
(a) 7
(b) 8
(c) 10
(d) n
Answer:
From the given table, it is clear that the sum of angles (interior angles) of a polygon with n sides = (n - 2) × 180°
(a) Here n = 7
∴ The sum of the angles of a polygon of 7 sides = (7 - 2) × 180°
= 5 × 180° = 900°

(b) Here n = 8
∴ The sum of the angles of a polygon of 8 sides = (8 - 2) × 180°
= 6 × 180°
= 1080°

(c) Here n = 10
∴ The sum of the angles of a polygon of 10 sides = (10 - 2) × 180°
= 8 ×180°
= 1440°

(d) It is clear- from the given table that the number of triangles is two less than the number of sides in the polygon. Therefore if the polygon has n sides, the number of triangles formed will be (n - 2).
The sum of angles of a triangle = 180°
∴ The sum of angles of a polygon of n sides = (n - 2) × 180°

Question 5.
What is a regular polygon? State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides
Answer:
A polygon is said to be a regular polygon, if all its,
(i) interior angles are equal;
(ii) sides are equal; and
(iii) exterior angles are equal.

The name of a regular polygon of
(i) 3 sides is equlateral triangle.
(ii) 4 sides is square
(iii) 6 sides is regular hexagon.

Question 6.
Find the angle measure x in the following figures:
(a)

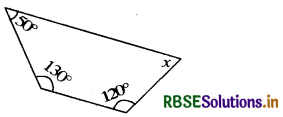
Answer:
We know that the sum of the angles (interior) of a quadrilateral is 360°.
∴ x + 120° + 130° + 50° = 360°
or x + 300° = 360°
or x = 360° - 300°
= 60°

(b)

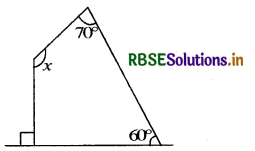
Answer:
We know that the sum of the angles (interior) of a quadrilateral is 360°.
∴ x + 70° + 60° + 90° = 360°
or x + 220° = 360°
or x = 360° - 220°
= 140°

(c)

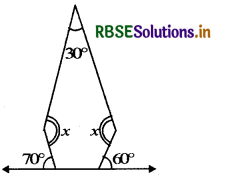
Answer:
According to question, the given figure has = (n - 2) × 180°
= (5 - 2) × 180°
= 3 × 180°
= 540°

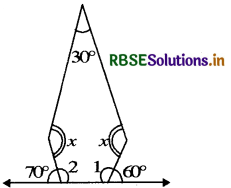
It is clear from the figure that
m∠1 + 60°= 180° [Linear pair]
or m∠1 = 180° - 60° = 120°
and m∠2 + 70°= 180° [Linear pair]
or m∠2 = 180° - 70° = 110°
∴ m∠1 + m∠2 + x + x + 30° = 540°
or 120° + 110° + 2x + 30° = 540°
or 2x + 260° = 540°
or 2x = 540° - 260°
= 280°
or x = \(\frac{540^{\circ}}{5}\) = 140°.

(d)

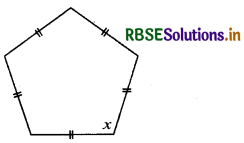
Answer:
According to question, the given figure has 5 sides, i.e. n = 5
∴ The sum of the angles of this figure = (n - 2) × 180°
= (5 - 2) × 180°
= 3 × 180° = 540°
∴ x + x + x + x + x = 540°
or 5x = 540°
or x = \(\frac{540^{\circ}}{5}\)
= 108°

Question 7.

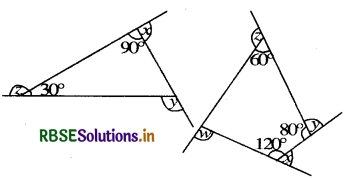
(a) Find x + y + z
(b) Find x + y + z + w
Answer:
(a) We know that the sum of the angles of a triangle is 180°,
∴ m∠ 1 + 30°,+ 90°= 180°
or m∠1 + 120°= 180°

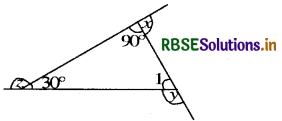
or m∠1 = 180° - 120°
= 60°
and x + 90° = 180° [Linear pair]
or x = 180° - 90°
= 90°
y + m∠1 = 180° [Linear pair]
or y + 60° = 180° [∵ m∠1 = 60°]
or y = 180° - 60° = 120° .......... (2)
and z + 30° = 180° [Linear pair]
or z = 180° - 30° = 150° ........... (3)
Adding (1), (2) and (3), we get
x + y + z = 90° + 120° + 150°
= 360°

(b) We know that the sum of the angles of a quadrilateral is 360°, therefore
m∠1 + 120° + 80° + 60°= 360°
or m∠1 + 260°= 360°
or m∠1 = 360° - 260° = 100°

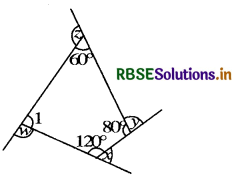
and x + 120°= 180° [Linear pair]
x = 180° - 120°
= 60° .......... (1)
y + 80°= 180° [Linear pair]
y= 180° - 80°
= 100° ........... (2)
z + 60°= 180° [Linear pair]
z = 180° - 60°
= 120° ............. (3)
m∠1 + w = 180° [Linear pair]
w = 180° - m∠1
= 180° - 100
= 80° ............ (4)
Adding (1), (2), (3) and (4)
x + y + z + w = 360°
60° + 100° + 120° + 80° = 360°