RBSE Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.5

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.5 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.5

Question 1.
Solve the following linear equations.
\(\frac{x}{2}-\frac{1}{5}=\frac{x}{3}+\frac{1}{4}\)
Answer:
Given, \(\frac{x}{2}-\frac{1}{5}=\frac{x}{3}+\frac{1}{4}\)
Denominators of both sides are 2, 3, 4 and 5.
LCM of 2, 3, 4 and 5= 60

Multiplying both sides by 60
60 × \(\left(\frac{x}{2}-\frac{1}{5}\right)\) = 60 × \(\left(\frac{x}{3}+\frac{1}{4}\right)\)
60 × \(\frac{x}{2}\) -60 × \(\frac{1}{5}\) = 60 × \(\frac{x}{3}\) + 60 × \(\frac{1}{4}\)
or 30x - 12 = 20x + 15
or 30x - 20x = 15 + 12
or 10x = 27
or x = \(\frac{27}{10}\)

Verification:
Putting x = \(\frac{27}{10}\) in the given equation
LHS = \(\frac{27}{10 \times 2}-\frac{1}{5}=\frac{27-4}{20}=\frac{23}{20}\)
and RHS = \(\frac{27}{10 \times 3}+\frac{1}{4}=\frac{9}{10}+\frac{1}{4}\)
= \(\frac{36+10}{40}=\frac{46}{40}=\frac{23}{20}\)
Hence, LHS = RHS

Question 2.
\(\frac{n}{2}-\frac{3 n}{4}+\frac{5 n}{6}\) = 21
Answer:
Given, \(\frac{n}{2}-\frac{3 n}{4}+\frac{5 n}{6}\) = 21
Denominators of both sides are 2, 4, 6 and 1
LCM of 2, 4, 6 and 1 = 12
Multiplying both sides by 12
12 × \(\left(\frac{n}{2}-\frac{3 n}{4}+\frac{5 n}{6}\right)\)
or 12 × \(\frac{n}{2}\) -12 × \(\frac{3n}{4}\) + 12 × \(\frac{5n}{6}\) = 252
or 6n - 9n + 10n = 252
or 7n = 252
or n = \(\frac{252}{7}\) = 36 

Verification:
Putting n = 36 in the given equation.
LHS = \(\frac{36}{2}-\frac{3 \times 36}{4}+\frac{5 \times 36}{6}\)
= 18 - 27 + 30 = 21 = RHS
Hence, LHS = RHS

Question 3.
x + 7 - \(\frac{8 x}{3}=\frac{17}{6}-\frac{5 x}{2}\)
Answer:
Given, x + 7 - \(\frac{8 x}{3}=\frac{17}{6}-\frac{5 x}{2}\)
Denominators of both sides are 1, 3, 6 and 2.
LCM of 1, 3, 6 and 2 = 6
Multiplying both sides by 6
6 × (x + 7 - \(\frac{8 x}{3}\)) = 6 × \(\left(\frac{17}{6}-\frac{5 x}{2}\right)\)
or 6 × x + 6 × 7 - 6 × \(\frac{8 x}{3}\) = 6 × \(\frac{17}{6}\) - 6 × \(\frac{5 x}{2}\)
or 6x + 42 - 16x = 17 - 15x
or 5x = - 25
or  x = \(\frac{-25}{5}\) = 5

Verification:
Putting x = - 5 in the given equation,

Hence, LHS = RHS

Question 4.
\(\frac{x-5}{3}=\frac{x-3}{5}\)
Answer:
Given \(\frac{x-5}{3}=\frac{x-3}{5}\)
Multiplying both sides by LCM of 3 and 5, i. e. 15
15\(\left(\frac{x-5}{3}\right)\) = 15\(\left(\frac{x-3}{3}\right)\)
or 5(x - 5) = 3(x-3)
or 5x - 25 = 3x - 9
or 5x - 3x = -9 + 25
or 2x = 16
or k = \(\frac{16}{2}\) = 8

Verification:
Putting x = 8 in given equation,
LHS = \(\frac{8-5}{3}=\frac{3}{3}\) = 1
and, RHS = \(\frac{8-5}{3}=\frac{3}{3}\) = 1
Hence, LHS = RHS

Question 5.
\(\frac{3 t-2}{4}-\frac{2 t+3}{3}=\frac{2}{3}\) - t
Answer:
Given, \(\frac{3 t-2}{4}-\frac{2 t+3}{3}=\frac{2}{3}\) - t
Multiplying both sides by LCM of 4 and 3, i.e. 12
12\(\left(\frac{3 t-2}{4}\right)\) - 12\(\left(\frac{2 t+3}{3}\right)\) = 12\( \left(\frac{2}{3}-t\right)\)
or 3(3t - 2) - 4(2t + 3) = 4(2 - 3t)
or 9t - 6 - 8t - 12 = 8 - 12t
t - 18 = 8 - 12t
or t + 12t = 8 + 18
or 13t = 26
or t = \(\frac{26}{13}\) = 2

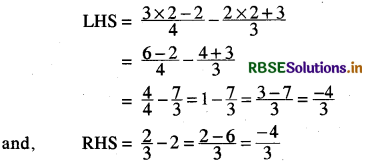
Hence, LHS = RHS

Question 6.
m - \(\frac{m-1}{2}\) = 1 - \(\frac{m-2}{3}\)
Answer:
Given, m - \(\frac{m-1}{2}\) = 1 - \(\frac{m-2}{3}\)
Multiplying both sides by LCM of 2 and 3, i.e. 6
6m - 6 × \(\left(\frac{m-1}{2}\right)\) = 6 - 6 × \(\left(\frac{m-2}{3}\right)\)
or 6m - 3 (m - 1) = 6 - 2 (m - 2)
or 6m - 3m + 3= 6 - 2m + 4
or 3m + 3 = - 2m + 10
or 3m + 2m = 10 - 3
or 5m = 7
or m = \(\frac{7}{5}\)

Verification:
Putting m = \(\frac{7}{5}\) is given equation

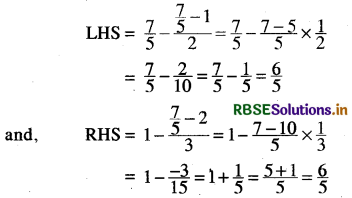
Hence, LHS = RHS

Question 7.
Simplify and solve the following linear equations. 
3(t - 3) = 5(2t + 1)
Answer:
Given, 3(t - 3) = 5(2t +1)
or 3t - 9 = 10t + 5
or 10t - 3t = - 9 - 5
or 7t = - 14
or t = -\(\frac{14}{7}\)
or t = -2

Question 8.
15(y - 4) - 2(y - 9) + 5(y + 6) = 0
Answer:
Given,
15(y - 4) - 2(y - 9) + 5(y + 6) = 0
15y - 60 - 2y + 18 + 5y + 30 = 0
or (15 - 2 + 5) y + (- 60 + 18 + 30) = 0
or 18y - 12 = 0
or 18y = 12
or y = \(\frac{12}{18}\)
y = \(\frac{2}{3}\)

Question 9.
3(5z - 7) - 2(9z - 11) = 4(8z - 13) - 17
Answer:
Given 3(5z - 7) - 2(9z - 11) = 4(8z - 13) - 17
or 15z - 21 - 18z + 22 = 32z - 52 - 17
or -3z - 32z = -69 - 1
or -35z = -70
or z = \(\frac{-70}{-35}\)
or z = 2

Question 10.
0.25(4f - 3) = 0.05 (10f - 9)
Answer:
Given,
or 0.25 (4f - 3)= 0.05(1 Of - 9)
or f - 0.75 = 0.5f - 0.45
or f - 0.5f= - 0.45 + 0.75
or (1 - 0.5)f = 0.3 8
or 0.5f = 0.3
or f = \(\frac{0.3}{0.5}\)
f = 0.6