RBSE Solutions for Class 8 Maths Chapter 2 एक चर वाले रैखिक समीकरण Ex 2.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 2 एक चर वाले रैखिक समीकरण Ex 2.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 2 एक चर वाले रैखिक समीकरण Ex 2.2

प्रश्न 1.
अगर आपको किसी संख्या से \(\frac{1}{2}\) घटाने और परिणाम को \(\frac{1}{2}\) से गुणा करने पर \(\frac{1}{8}\) प्राप्त होता है, तो वह संख्या क्या है?
हल:
माना वह संख्या x है,

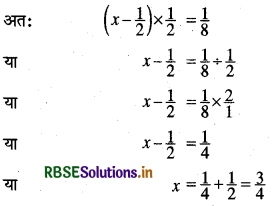
∴ वांछित संख्या में है।

प्रश्न 2.
एक आयताकार तरणताल (Swimming Pool) की लम्बाई उसकी चौड़ाई के दुगुने से 2 मीटर अधिक है। यदि इसका परिमाप 154 मीटर है, तो इसकी लम्बाई व चौड़ाई ज्ञात कीजिए।
हल:
माना तरणताल की चौड़ाई x मीटर हो तो लम्बाई
= (2x + 2) मीटर परिमाप
= 2(लम्बाई + चौड़ाई)
= 2(2x + 2 + x)
= 4x + 4 + 2x 
= 6x +4 
लेकिन, प्रश्नानुसार परिमाप 154 मीटर है।
∴ 6x + 4 = 154 
6x = 154 - 4
6x = 150
या x = \(\frac{150}{6}\) = 25
लम्बाई = (2 × 25 + 2) मीटर = 52 मीटर
और, चौड़ाई = 25 मीटर 

प्रश्न 3.
एक समद्विबाहु त्रिभुज का आधार 3 cm तथा उसका परिमाप 4\(\frac{2}{15}\) cm है। उसकी दो बराबर भुजाओं की माप ज्ञात कीजिए।
हल:
माना समद्विबाहु त्रिभुज ABC की प्रत्येक समान भुजा की लम्बाई x cm है।

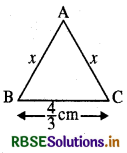
तो इसका परिमाप = AB + BC + CA:
= (x + \(\frac{4}{3}\) + x)cm
= (2x + \(\frac{4}{3}\))cm

लेकिन, प्रश्नानुसार परिमाप =4\(\frac{2}{15}\)cm = \(\frac{62}{15}\)cm
2x + \(\frac{4}{3}\) = \(\frac{62}{15}\)
या (2x + \(\frac{4}{3}\)) × 15 = \(\frac{62}{15}\) × 15
या 30x + 20 = 62
(दोनों पक्षों को 15 से गुणा करने पर)
या 30x = 62 - 20
या 30x = 42
x = \(\frac{42}{30}=\frac{7}{5} = 1 \frac{2}{5}\)
अतः प्रत्येक भुजा = 1\( \frac{2}{5}\)cm 

प्रश्न 4.
दो संख्याओं का योग 95 है। यदि एक संख्या दूसरी से 15 अधिक है तो दोनों संख्याएँ ज्ञात कीजिए।
हल:
माना कि एक संख्या x है, तो दूसरी संख्या x + 15
प्रश्नानुसार x + (x + 15) = 95
या 2x + 15 = 95
या 2x + 15 - 15 = 95 - 15
(दोनों पक्षों में से 15 घटाने पर)
या 2x = 80
या \(\frac{2 x}{2}=\frac{80}{2}\)
(दोनों पक्षों में 2 से भाग देने पर)
या x = 40
अतः संख्याएँ 40 और (40 + 15) = 55 हैं। 

प्रश्न 5.
दो संख्याओं में अनुपात 5 : 3 है। यदि उनमें अन्तर 18 है, तो संख्याएँ ज्ञात कीजिए।
हल:
माना संख्याएँ 5x और 3x हैं।
प्रश्नानुसार 5x - 3x = 18
या 2x = 18
या x = \(\frac{18}{2}\) =9
x = 9 का मान रखने पर संख्याएँ-
प्रथम संख्या 5x = 5 × 9 = 45
दूसरी संख्या 3x = 3 × 9 = 27

प्रश्न 6.
तीन लगातार पूर्णांकों का योग 51 है। पूर्णांक ज्ञात कीजिए।
हल:
माना तीन लगातार संख्याएँ x, (x + 1) और (x + 2)
प्रश्नानुसार
या x + (x + 1) + (x + 2) = 51
या 3x + 3 = 51
या 3x = 51 - 3 = 48
या x = \(\frac{48}{3}\) =16 अतः तीन लगातार संख्याएँ 16, 17 और 18 हैं।

प्रश्न 7.
8 के तीन लगातार गुणजों का योग 888 है। गुणजों को ज्ञात कीजिए।
हल:
माना 8 के तीन लगातार गुणज 8x, 8(x + 1) और 8(x + 2) हैं।
प्रश्नानुसार 8x + 8(x + 1) + 8(x + 2) = 888
या 8x+ 8x + 8+ 8x + 16 = 888
या 24x + 24 = 888
या 24x = 888 - 24
या 24x = 864
या x = \(\frac{864}{24}\) = 36
अतः गुणज 8 × 36, 8 × (36 + 1) और 8 × (36 + 2) 
अर्थात् 288, 296 और 304 हैं।

प्रश्न 8.
तीन लगातार पूर्णांक बढ़ते क्रम में लेकर उन्हें क्रमशः 2, 3 तथा 4 से गुणा कर योग करने पर योगफल 74 प्राप्त होता है। तीनों पूर्णांक ज्ञात कीजिए।
हल:
माना तीन लगातार पूर्णांक x, (x + 1) और (x + 2) हैं।
प्रश्नानुसार 2 × x + 3 × (x + 1) + 4 × (x + 2) = 74 
या 2x + 3x + 3 + 4x + 8 = 74
या 9x + 11 = 74
या 9x= 74 - 11
या 9x= 63
या x = \(\frac{63}{9}\) = 7
अतः संख्याएँ 7, 8 और 9 हैं।

प्रश्न 9.
राहुल और हारुन की वर्तमान आयु में अनुपात 5:7 है। चार वर्ष बाद उनकी आयु का योग 56 वर्ष हो जाएगा। उनकी वर्तमान आयु क्या है?
हल:
माना राहुल और हारुन की आयु 5x और 7x वर्ष है। 
चार वर्ष बाद-राहुल की आयु = 5x +4
और, हारुन की आयु = 7x+4 
प्रश्नानुसार, (5x+4) + (7x+ 4) = 56
या 12x + 8 = 56
या 12x = 56 - 8
या 12x = 48
या x = 48 = 4
राहुल की आयु = 5 × 4 = 20 वर्ष 
और हारुन की आयु = 7 × 4 = 28 वर्ष

प्रश्न 10.
किसी कक्षा में बालक और बालिकाओं की संख्याओं में अनुपात 7:5 है। यदि बालकों की संख्या बालिकाओं की संख्या से 8 अधिक है तो कक्षा में कुल कितने विद्यार्थी हैं?
हल:
माना कक्षा में बालकों और बालिकाओं की संख्याएँ क्रमशः 7x और 5x हैं। प्रश्नानुसार
या 7x = 5x +8
या 7x - 5x = 8
या 2x = 8 या
या x = 4
∴ बालकों की संख्या = 7 × 4 = 28
और बालिकाओं की संख्या = 5 × 4 = 20
अतः कक्षा में कुलं विद्यार्थी 28 + 20 अर्थात् 48 हैं। 

प्रश्न 11.
बाइचुंग के पिताजी उसके दादाजी से 26 वर्ष छोटे हैं और उससे 29 वर्ष बड़े हैं। यदि उन तीनों की आयु का योग 135 वर्ष है, तो उनकी आयु अलग-अलग ज्ञात कीजिए।
हल:
माना बाइचुंग की आयु x वर्ष तो
बाइचुंग के पिताजी की आयु = (x + 29)
बाइचुंग के दादाजी की आयु = [(x + 29) + 26] वर्ष
= (x+ 55) वर्ष

प्रश्नानुसार x + (x + 29) + (x + 55) = 135
या 3x + 84 = 135
या 3x = 135-84
या 3x = 51 या
या x = \(\frac{51}{3}\) = 17 
∴ बाइचुंग की आयु 17 वर्ष
उसके पिताजी की आयु 17 + 29 = 46 वर्ष
उसके दादाजी की आयु 17 + 55 = 72 वर्ष

प्रश्न 12.
15 वर्ष बाद रवि की आयु, उसकी वर्तमान आयु से चार गुनी हो जाएगी।रवि की वर्तमान आयुक्या
हल:
माना रवि की वर्तमान आयु x वर्ष है।
15 वर्ष बाद रवि की आयु (x + 15) वर्ष
15 वर्ष बाद रवि की आयु, वर्तमान आयु की चार गुना होगी।
या 4x = x + 15
या 4x - x = 15
या 3x = 15
या x = \(\frac{15}{3}\) = 5
अतः रवि की वर्तमान आयु 5 वर्ष है।

प्रश्न 13.
एक परिमेय संख्या को \(\frac{5}{2}\) से गुणा कर \(\frac{2}{3}\) जोड़ने पर \(\frac{-7}{12}\) प्राप्त होता है। वह संख्या क्या है?
हल:
माना वांछित संख्या x है.
अतः प्रश्नानुसार, x × \(\frac{5}{2}+\frac{2}{3}=-\frac{7}{12}\)
या \(\frac{5}{2}\) x = \(-\frac{7}{12}-\frac{2}{3}\)
या \(\frac{5}{2}\) x = \(\frac{-7-8}{12}\)
या \(\frac{5}{2}\) x = \(\frac{-15}{12}\)
या x = \(\frac{-15}{12} \times \frac{2}{5}=-\frac{1}{2}\)
अतः वांछित संख्या \(-\frac{1}{2}\) है। 

प्रश्न 14.
लक्ष्मी एक बैंक में खजांची है। उसके पास नकदी के रूप में 100 रुपए, 50 रुपए और 10 रुपए वाले नोट हैं। उनकी संख्याओं में क्रमशः 2 : 3:5 का अनुपात है और उनका कुल मूल्य 4,00,000 रुपए है। उसके पास प्रत्येक प्रकार के कितने-कितने नोट हैं?
हल:
माना 100 रुपए, 50 रुपए और 10 रुपए के क्रमशः 2x, 3x और 5x नोट हैं।
अब 100 रुपए के 2x नोटों का मान = (2x × 100) रुपए
= 200x रुपए

50 रुपए के 3x नोटों का मान = (3x × 50) रुपए
= 150x रुपए

और 10 रुपए के 5x नोटों का मान = (5x × 10) रुपए.
= 50x रुपए

लेकिन कुल राशि 4,00,000 रुपए 
∴ 200x + 150x + 50x = 400000
या 400x = 400000
या x = 1000
अतः,100 रु. के नोटों की संख्या = 2x = 2 × 1000
= 2000
50 रु. के नोटों की संख्या = 3x = 3 × 1000
= 3000
और 10 रु. के नोटों की संख्या = 5x = 5 × 1000
= 5000

प्रश्न 15.
मेरे पास 300 रुपए मूल्य के, 1 रुपए, 2 रुपए और 5 रुपए वाले सिक्के हैं। 2 रुपए वाले सिक्कों की संख्या 5 रुपए वाले सिक्कों की सख्या की तिगुनी है और सिक्कों की कुल संख्या 160 है। मेरे पास प्रत्येक प्रकार के कितने-कितने सिक्के हैं?
हल:
माना 5 रुपए के सिक्कों की संख्या x है तो
2 रुपए के सिक्कों की संख्या = 3x
और 1 रुपए के सिक्कों की संख्या = 160 - x - 3x
= 160 - 4x

अब, 5 रुपए के सिक्कों का मान = (5 × x) रुपए
= 5x रुपए

2 रुपए के सिक्कों का मान = (2 × 3x) रुपए
= 6x रुपए

और 1 रुपए के सिक्कों का मान = 1 × (160 - 4x) रु.
= (160 - 4x) रुपए
लेकिन कुल राशि = 300 रुपए 5x + 6x + (160 - 4x) = 300
7x = 300 - 160 7x= 140
x = 20

अतः,5 रु. के सिक्कों की संख्या = x = 20
2 रु. के सिक्कों की संख्या = 3x
= 3 × 20 = 60
और, 1 रु. के सिक्कों की संख्या = 160 - 4x
= 160 - (4 × 20)
= 160 - 80 = 80

प्रश्न 16.
एक निबंध प्रतियोगिता में आयोजकों ने तय किया कि प्रत्येक विजेता को 100 रुपए और विजेता को छोड़कर प्रत्येक प्रतिभागी को 25 रुपए पुरस्कार के रूप में दिए जाएंगे। यदि पुरस्कारों में बाँटी गई राशि 3,000 रुपए थी तो कुल 63 प्रतिभागियों में विजेताओं की संख्या ज्ञात कीजिए।
हल:
माना विजेताओं की संख्या x है तो तो प्रतिभागियों की संख्या (63 - x)
विजेता x प्रतिभागियों की कुल राशि = (100 × x) रुपए
= 100 रुपए 

और (63 - x) प्रतिभागियों को बाँटी गई राशि
= 25(63 -x) रु. 

लेकिन कुल बाँटी गई राशि = 3000 रुपए
100x + 25(63 - x) = 3000 रुपए
4x + (63 - x) = 120
(दोनों पक्षों में 25 से भाग देने पर)
या 3x + 63 = 120
या 3x = 120 - 63
या 3x = 57
या x = \(\frac{57}{3}\) = 19 
∴ विजेताओं की संख्या 19 है।