RBSE Solutions for Class 8 Maths Chapter 16 संख्याओं के साथ खेलना Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 16 संख्याओं के साथ खेलना Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 16 संख्याओं के साथ खेलना Intext Questions

(प्रयास कीजिए - पृष्ठ 260)

प्रश्न 1.
निम्नलिखित संख्याओं को व्यापक रूप में लिखिए
(i) 25
हल:
25 = 20 + 5 = 10 × 2 + 1 × 5

(ii) 73
हल:
73 = 70 + 3 = 10 × 7 + 1 × 3

(iii) 129
हल:
129 = 100 + 20 +9 = 100 × 1 + 10 × 2 + 1 × 9

(iv) 302
हल:
302 = 300 + 00 + 2 = 100 × 3 + 10 × 0 + 1 × 2

प्रश्न 2.
निम्नलिखित को सामान्य रूप में लिखिए
(i) 10 × 5 + 6
हल:
10 × 5 + 6 = 50 + 6 = 56

(ii) 100 × 7 + 10 × 1 + 8
हल:
100 × 7 + 10 × 1 + 8 = 700 + 10 + 8 = 718

(ii) 100a + 10c + b
हल:
100a + 10c + b = acb

(प्रयास कीजिए - पृष्ठ 261-I)

प्रश्न 1.
जाँच कीजिए कि यदि सुंदरम ने निम्नलिखित संख्याएँ चुनी होतीं, तो परिणाम क्या प्राप्त होते है
1. 27 
हल:
माना कि सुंदरम संख्या 27 चुनता है। अतः उसे उलटी संख्या 72 प्राप्त होती है, वह इन दोनों संख्याओं को जोड़कर 27 + 72 = 99 प्राप्त करता है। अंत में वह इस संख्या को 11 द्वारा विभाजित करता है, 99 ÷ 11 = 9 प्राप्त करता है जिसमें कुछ शेषफल नहीं बचता। इस प्रकार, भागफल 9 चुनी गई संख्या के अंकों का योग है (∵ 2 +7 = 9)।

2. 39 
हल:
माना कि सुंदरम 39 चुनता है। अतः उसे उलटी संख्या 93 प्राप्त होती है। वह इन दोनों संख्याओं को जोड़कर 39 + 93 = 132 प्राप्त करता है। अंत में वह इस संख्या को 11 द्वारा विभाजित करके 132 ÷ 11 = 12 प्राप्त करता है तथा कोई शेषफल नहीं होता है।
इस प्रकार, भागफल 12 = चुनी गई संख्या के अंकों का योग (∵ 3 + 9 = 12)

3. 64
हल:
माना कि सुंदरम संख्या 64 चुनता है। अतः उसे उलटी संख्या 46 प्राप्त होती है। वह इन दोनों संख्याओं को जोड़कर 64 + 46 = 110 प्राप्त करता है। अंत में वह इस संख्या को 11 द्वारा विभाजित करके 110 ÷ 11 = 10, शेषफल शून्य के साथ प्राप्त करता है। इस प्रकार, भागफल 10 = चुनी गई संख्या के अंकों का योग (∵ 6 + 4 = 10)

4. 17
हल:
माना कि सुंदरम संख्या 17 चुनता है। अतः उसे उलटी संख्या 71 प्राप्त होती है। वह इन दोनों संख्याओं को जोड़कर 17 + 71 = 88 प्राप्त करता है। अंत में वह इस संख्या को 11 से विभाजित करके 88 ÷ 11 = 8, शेषफल शून्य के साथ प्राप्त करता है। इस प्रकार, भागफल 8 = चुनी गई संख्या के अंकों का योग (∵ 1 + 7 = 8)

(पृष्ठ 261-II)

प्रश्न 1.
जाँच कीजिए कि यदि सुंदरम ने उपर्युक्त के लिए निम्नलिखित संख्या चुनी होती, तो क्या परिणाम प्राप्त होते
1. 17
हल:
माना कि सुंदरम संख्या 17 सोचता है। अतः उसकी गणनाएँ निम्नानुसार होंगी-पहले उसे संख्या 71 प्राप्त होगी। इसके बाद 71 - 17 = 54; और अंत में वह 54 ÷ 9 = 6 प्राप्त करता है जिसमें शेषफल शून्य आता है, वह देखता है कि 6 = 7 - 1, अर्थात् वह संख्याओं के बीच अन्तर चुनता है।

2. 21
हल:
माना कि सुंदरम संख्या 21 सोचता है। अतः उसकी गणनाएँ निम्नानुसार होंगी-पहले उसे संख्या 12 प्राप्त होगी; इसके बाद 21 - 12 = 9; और अंत में वह 9 ÷ 9 = 1 प्राप्त करता है, शेषफल शून्य के साथ, वह देखता है कि 1 = 2 - 1 अर्थात् वह संख्याओं के बीच अन्तर चुनता है।

3. 96
हल:
माना कि सुंदरम संख्या 96 सोचता है। अतः उसकी गणनाएँ निम्नानुसार होंगी-पहले उसे संख्या 69 प्राप्त होगी; इसके बाद 96 - 69 = 27; और अंत में वह 27 ÷ 9 = 3 प्राप्त करता है, शेषफल शून्य के साथ, वह देखता है कि 3 = 96, अर्थात् वह संख्याओं के बीच अन्तर चुनता है।

4. 37
हल:
माना कि सुंदरम संख्या 37 सोचता है। अतः उसकी गणनाएँ निम्नानुसार होंगी-पहले उसे संख्या 73 प्राप्त होगी; इसके बाद 73 - 37 = 36; और अंत में वह 36 ÷ 9 = 4 प्राप्त करता है, शेषफल शून्य के साथ, वह देखता है कि 4 = 7 - 3, अर्थात् वह संख्याओं के बीच अन्तर चुनता है।

(प्रयास कीजिए - पृष्ठ 262)

प्रश्न 1.
जाँच कीजिए कि यदि मीनाक्षी ने निम्नलिखित संख्याएँ चुनी होती, तो परिणाम क्या प्राप्त होता? प्रत्येक स्थिति में, अंत में प्राप्त हुए भागफल का एक रिकॉर्ड (record) रखिए।
1. 132
हल:
माना कि मीनाक्षी संख्या चुनती है 132; अत: उसे प्राप्त होती है उलटी संख्या : 231 दोनों का अन्तर : 231 – 132 = 99 विभाजन : 99 ÷ 99 = 1, शेषफल रहित। अतः, उसे भागफल 1 प्राप्त होता है, और वह देखती है कि 1 = 2 - 1, अर्थात् भागफल सैकड़े के अंक और इकाई के अंक के बीच के अन्तर के बराबर है। 

2. 469
हल:
माना कि मीनाक्षी संख्या चुनती है 469, अतः उसे प्राप्त होती है उलटी संख्या : 964 दोनों का अन्तर : 964 - 469 = 495 विभाजन : 495 ÷ 99 = 5, शेषफल रहित। अतः, उसे भागफल 5 प्राप्त होता है और वह देखती है कि 5 = 9-4, अर्थात् भागफल इकाई के अंक और सैकड़े के अंक के बीच के अन्तर के बराबर है।

3. 737
हल:
माना कि मीनाक्षी संख्या चुनती है 737, अतः उसे प्राप्त होती है उलटी संख्या : 737 दोनों का अन्तर : 737 - 737 = 0 विभाजन : 0 ÷ 99 = 0, शेषफल रहित। अतः, उसे भागफल 0 प्राप्त होता है, और वह देखती है कि 0 = 7-7, अर्थात् भागफल इकाई के अंक और सैकड़े के अंक के बीच के अन्तर के बराबर है।

4. 901
हल:
माना कि मीनाक्षी संख्या चुनती है 901, अतः उसे प्राप्त होती है उलटी संख्या : 109 दोनों का अन्तर : 901 - 109 = 792 विभाजन : 792 ÷ 99 = 8 शेषफल रहित। अतः, उसे भागफल 8 प्राप्त होता है, और वह देखती है कि 8 = 9 - 1 अर्थात् भागफल इकाई के अंक और सैकड़े के अंक के बीच के अन्तर के बराबर है।

(प्रयास कीजिए - पृष्ठ 263)

प्रश्न 1.
जाँच कीजिए कि यदि सुंदरम ने निम्नलिखित संख्याएँ सोची होती, तो परिणाम क्या प्राप्त होता? 
1. 417
हल:
माना कि चुनी गई संख्या 417 है। 4, 1,7 अंकों के प्रयोग द्वारा 3-अंकों की दो और संख्याएँ प्राप्त की जो हैं : 741 और 174 
इन संख्याओं को जोड़ने पर, हमें प्राप्त होती है

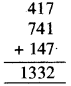
1332 को 37 से विभाजित करने पर, 
1332 ÷ 37 = 36, शेषफल रहित। 

2. 632
हल:
माना कि चुनी गई संख्या 632 है।
6,3,2 अंकों के प्रयोग द्वारा 3 अंकों की दो और संख्याएँ प्राप्त की जो हैं : 263 और 326 
इन संख्याओं को जोड़ने पर, हमें प्राप्त होती है

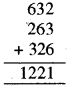
1221 को 37 से विभाजित करने पर, 
1221 ÷ 37 = 33, शेषफल रहित। 

3. 117
हल:
माना कि चुनी गई संख्या 117 है। 1, 1,7 अंकों के प्रयोग द्वारा 3 अंकों की दो और संख्याएँ प्राप्त की, जो हैं : 711 और 171 
इन संख्याओं को जोड़ने पर, हमें प्राप्त होती है

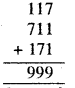
999 को 37 से विभाजित करने पर, 
999 ÷ 37 = 27, शेषफल रहित। 

4. 937
हल:
माना कि चुनी गई संख्या 937 है। 9, 3, 7 अंकों के प्रयोग द्वारा 3 अंकों की 2 और संख्याएँ प्राप्त की, जो हैं : 793 और 379
इन संख्याओं को जोड़ने पर,

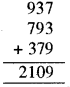
2109 को 37 से विभाजित करने पर, 
2109 ÷ 37 = 57, शेषफल रहित।

(प्रयास कीजिए - पृष्ठ 270)

प्रश्न 1.
निम्नलिखित संख्याओं की 9 से विभाज्यता की जाँच कीजिए
1. 108
2. 616
3. 294
4. 432
5. 927
हल:
9 के भाजकता के नियम से हम जानते हैं कि कोई संख्या 9 से विभाज्य होती है यदि उसके अंकों का योग 9 से विभाज्य हो।
अतः
1. दी गई संख्या = 108 इसके अंकों का योग = 1 + 0 + 8 = 9, जो 9 से विभाज्य है।
अतः, 108 संख्या 9 से विभाज्य है।

2. दी गई संख्या = 616 इसके अंकों का योग = 6 + 1 + 6 = 13, जो 9 से अविभाज्य है।
अतः, 616 संख्या 9 से विभाज्य नहीं है।

3. दी गई संख्या = 294 इसके अंकों का योग = 2 + 9 + 4 = 15, जो 9 से अविभाज्य है।
अतः, 294 संख्या 9 से विभाज्य नहीं है।

4. दी गई संख्या = 432 इसके अंकों का योग = 4 + 3 + 2 = 9, जो 9 से विभाज्य
अतः, 432 संख्या 9 से विभाज्य है।

5. दी गई संख्या = 927 इसके अंकों का योग = 9+2+7 = 18, जो 9 से विभाज्य
अतः, 927 संख्या 9 से विभाज्य है।

(प्रयास कीजिए - पृष्ठ 271)

प्रश्न 1.
निम्नलिखित संख्याओं की 3 से विभाज्यता की जाँच कीजिए
1. 108 
2. 616 
3. 294 
4.432
5. 927
हल:
3 के भाजकता के नियम से हम जानते हैं कि कोई संख्या 3 से विभाज्य होती है यदि उसके अंकों का योग 3 से विभाज्य हो। अतः
1. दी गई संख्या = 108 इसके अंकों का योग = 1 + 0 + 8 = 9, जो 3 से विभाज्य है।
अतः 108 संख्या 3 से विभाज्य है।

2. दी गई संख्या = 616 इसके अंकों का योग = 6 + 1 + 6 = 13, जो 3 से अविभाज्य है।
अतः 616 संख्या 3 से अविभाज्य है।

3. दी गई संख्या = 294 इसके अंकों का योग = 2 + 9 + 4 = 15, जो 3 से विभाज्य है।
अतः 294 संख्या 3 से विभाज्य है।

4. दी गई संख्या = 432 इसके अंकों का योग = 4+ 3 + 2 = 9, जो 3 से विभाज्य है।
अतः 432 संख्या 3 से विभाज्य है।

5. दी गई संख्या = 927 इसके अंकों का योग = 9 + 2 + 7 = 18, जो 3 से विभाज्य है। 
अतः, 927 संख्या 3 से विभाज्य है।