RBSE Solutions for Class 8 Maths Chapter 16 Playing with Numbers Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 16 Playing with Numbers Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 16 Playing with Numbers Intext Questions

(Try These - Page 250)

Question 1.
Write the following numbers in generalised form:
(i) 25
Answer:
25 = 20 + 5 = 10 × 2 + 1 × 5

(ii) 73
Answer:
73 = 70 + 3 = 10 × 7 + 1 × 3

(iii) 129
Answer:
129 = 100 + 20 + 9 = 100 × 1 + 10 × 2 + 1 × 9

(iv) 302
Answer:
302 = 300 + 00 + 2 = 100 × 3 + 10 × 0 + 1 × 2

Question 2.
Write the following in the usual form:
(i)    10 × 5 + 6
Answer:
10 x5 + 6 = 50 + 6 = 56

(ii) 100 × 7 + 10 × 1 + 8
Answer:
100 × 7 + 10 × 1 + 8 = 700 + 10 + 8 = 718

(iii) 100a + 10c + 6
Answer:
100a + 10c + 6 = acb

(Try These - Page 251)

Question 1.
Check what the result would have been if Sundaram had chosen the numbers shown below:
1. 27
Answer:
The given number = 27 
Reversing the digits, we get = 72 
Sum of die two numbers = 27 + 72 = 99 
99 ÷ 11 = 9;
Remainder = 0
Also, 99 = 11 × 9 =11 (2 + 7)
= 11 (Sum of digits of die given number).

2. 39
Answer:
Given number = 39 
Reversing the digits, we get = 93
Sum of die two numbers = 39 + 93 = 132
Now, 132 ÷ 11 = 12; Remainder = 0 
Also, 132 = 11 × 12 = 11 (12) = 11 (3 + 9) 
= 11 (Sum of digits of the given number)

3. 64
Answer:
Given number = 64 
Reversing the digits, we get = 46
Sum of die two numbers = 64 + 46 = 110 
Now, 110 = 11(10) = 11 (6 + 4) and 110 ÷ 11 = 10,
Remainder = 0 Therefore 110 = 11 (Sum of digits of the given number)

4. 17
Answer:
Given number =17
Reversing the digits, we get = 71
Sum of the two numbers = 17 + 71 = 88 88 ÷ 11 = 8, 
Remainder = 0 Also, 88 = 11 × 8 = 11 (1 + 7)
= 11 (Sum of digits of the given number) Hence, the remainder in each case is zero.

(Page 251)

Question 1.
Check what the result would have been if Sundaram had chosen the numbers shown below—
1. 17
Answer:
Given number = 17
Reversing the number = 71
Subtract the smaller number from bigger = 71 - 17 = 54
and, 54 = 9 = 6, remainder = 0
∴ a - b or b - a = 7 - 1 = 6; i.e., the difference between the number he choose.

2. 21
Answer:
Given number = 21
. Reversing the number = 12 Subtract the smaller number from bigger = 21 - 12 = 9
and 9 = 9 = 1, remainder = 0
∴ a - b or b - a = 2 - 1 = 1; i.e., the difference between the number he choose.

3. 96
Answer:
Given number = 96 Reversing the number = 69
Subtract the smaller number from bigger = 96 - 69 = 27
and 27 = 9 = 3, remainder = 0
∴ a - b or b - a = 9 - 6 = 3; i.e., the
difference between the number he choose.

4. 37
Answer:
Given number = 37 Reversing the number =73
Subtract the smaller number from bigger = 73 - 37 = 36, and 36 = 9 = 4 remainder = 0
∴ a - b or b - a = 7 - 3 = 4; i.e., the difference between the number he choose.
Hence, difference between the given number and reversed number = Multiple of 9.

(Try These - Page 2521)

Question 1.
Check what the result would have been if Minakshi had chosen the numbers shown below. In each case keep a record of the quotient obtained at the end.
1. 132
Answer:
Let the Minakshi had chosen the 3-digit number 132.
Then Reversed number = 231,
Difference = 231 - 132 = 99 and 99 ÷ 99 = 1, Remainder = 0

2. 469
Answer:
Here, Given Number = 469 
Reversed Number = 964 
Difference = 964 - 469 = 495 and 495 ÷ 99 = 5, Remainder = 0

3. 737
Answer:
Given Number =737 
Reversed Number =737
and Difference = 737 - 737 = 0
0 ÷ 99 = 0, Remainder = 0

4. 901
Answer:
Given Number = 901
Reversed Number = 109
Difference = 901 - 109 = 792 and 792 ÷ 99 = 8,
Remainder = 0 Hence, If a > c, then,
(100a + 10b + c) - (100c + 10b + a) = 99(a - c) i.e., the resulting number is divisible by 99 in each case and the quotient obtained is [(c - a) or (a - c)]. So, the remainder is zero.

(Try These - Page 253)

Question 1.
Check what the result would have been if Sundaram had chosen the numbers shown below.
1. 417
Answer:
Let the number chosen be 417. 
Two more 3-digit numbers obtained by using the digits 4, 1, 7 are 741 and 174.
On adding these numbers, we get

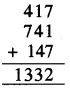
On dividing 1332 by 37, we get 1332 ÷ 37 = 36, remainder = 0

2. 632
Answer:
Let the number chosen be 632.
Two more 3-digit numbers obtained by using the digits 6, 3, 2 are 263 and 326.
On adding these numbers, we get

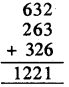
Now 1221 ÷ 37 = 33, remainder = 0

3. 117
Answer:
Let the number chosen be 117
Two more 3-digit numbers obtained by using the digits 1, 1, 7 are 711 and 171.
Or, adding these number, we get 
117 + 711 + 171 = 999
and 999 ÷ 37 = 27, remainder = 0

4. 937
Answer:
Let the number chosen be 937.
Two more 3-digit numbers obtained by using the digits 9, 3, 7 are 793 and 379.
On adding these numbers, we get 937 + 793 + 379 = 2109
and 2109 4 37 = 57, remainder = 0
Hence, abc is a 3-digit number then abc + cab + bca - 111 (a + b + c)
= 37 × 3 (a + b + c) which is divisible by 37.

(Do This - Page 255)

Question 1.
Write a two digit number ab and the number obtained by reversing its digits, i.e. ba. Find their sum. Let the sum be a 3-digit number dad.
i.e. ab + ba = dad 
(10a + b) + (10b + a) = dad 
11(a + b) = dad
The sum a + b cannot exceed 18 (why) 
Is dad a multiple of 11?
Is dad less than 198 ?
Write all the 3-digit numbers which are multiples of 11 upto 198.
Find the value of a and d.
Answer:
The values of a and b cannot be greater than 9.
The sum of a + b can not exceed 18.
Yes, dad is a multiple of 11 as dad is a product of 11 and {a + b).
∵ Greatest two digit numbers is 99.

Therefore, suin of any two digit numbers can not be greater than 18.
Hence dad is less than 198.
All three digit numbers which are multiples of 11 upto 198 are 110, 121, 132, 143, 154, .165, 176, 187 and 198
Clearly dad =121
⇒ d = 1, a = 2
 
(Try These - Page 257)

Question 1.
If the division N ÷ 5 leaves a remainder of 3, what might be the ones digit of N?
(The ones digit, when divided by 5, must leave a remainder of 3. So the ones digit must be either 3 or 8.)
Answer:
Do yourself.

Question 2.
If the division N ÷ 5 leaves a remainder of 1, what might be the ones digit of A?
Answer:
The ones digit when divided by 5, must leave a remainder of 1 so the ones digit of N must be either 1 or 6,

Question 3.
If the division N ÷ 5 leaves a remainder of 4, what might be the ones digit of N?
Answer:
The ones digit, when divided by 5, must leave a remainder of 4. So the ones digit must be either 4 or 9.

(Page 257 - 258)

Question 1.
If the division N ÷ 2 leaves a remainder of 1, what might be the ones digit of N?
(N is odd; so its ones digit is odd. Therefore, the ones digit must be 1, 3, 5, 7 or 9.)
Answer:
Do yourself.

Question 2.
If the division N ÷ 2 leaves no remainder (i.e., zero remainder), what might be the one’s digit of N ?
Answer:
If the division N ÷ 2 leaves no remainder then it means that N is even, so its unit digit is also even.
Therefore the ones digit must be 0, 2, 4, 6 or 8.

Question 3.
Suppose that the division N ÷ 5 leaves a remainder of 4 and the division N ÷ 2 leaves a remainder of 1. What must be the one’s digit of N ?
Answer:
The division N ÷ 5 leaves a remainder of 4.
∴ The ones digit when divided by 5 must leave a remainder of 4,
Therefore the ones digit must be either 4 or 9.    ... (1)
Again The division N ÷ 2 leave a remainder 1
N is odd, so its unit digit is odd.
∴ The ones digit of N must be 1, 3, 5, 7 or 9    ... (2)
By (1) and (2)
The ones digit must be 9.

(Think, Discuss And Write - Page 259)

Question 1.
You have seen that a number 450 is divisible by 10. It is also divisible by 2 and 5 which are factors of 10. Similarly, a number 135 is divisible by 9. It is also divisible by 3 which is a factor of 9.
Can you say that if a number is divisible by any number m, then it will also be divisible by each of the factors of m?
Answer:
Yes, we can say that if a number is divisible by any number m, then it will also be divisible by each of the factors of m.

Question 2.
(i) Write a 3-digit number abc as 100a + 106 + c
= 99a + 11 b + (a - b + c)
= 11(9a + 6) + (a - b + c)
If the number abc is divisible by 11, then what can you say about (a - b + c)?
Is it necessary that (a + c - b) should be divisible by 11?
Answer:
(a - b + c) is also divisible by 11.

(ii)    Write a 4-digit number abed as 1000a + 1006 + 10c + d
= (1001a + 99b + 11c) - (a - b + c - d)
= 11(91a + 9b + c) + [(b + d) - (a + c)]
If the number abed is divisible by 11, then what can you say about [(b + d) - (a + c)]?
Answer:
[(b + d) - (a + c)] is divisible by 11.

(iii) From (i) and (ii) above, can you say that a number will be divisible by 11 if the difference between the sum of digits at its odd places and that of digits at the even places is. divisible by 11?
Answer:
Yes, we can say that a number is divisible by 11 if the difference between the sum of digits at its odd places and that of digits at the even places is divisible by 11.

(Try These - Page 260)

Question 1.
Check the divisibility of the following numbers by 9
1. 108
Answer:
Given number = 108
∵ Sum of digits = 1 + 0 + 8 = 9
and 9 + 9=1, remainder = 0
∴ 108 is divisible by 9.

2. 616
Answer:
Given number =616
∵ Sum of digits = 6 + 1 + 6 = 13,
13 is not divisible by 9.
∴ 616 is also not divisible by 9.

3. 294
Answer:
Given number = 294
Sum of digits = 2 + 9 + 4= 15
15 is not divisible by 9.
∴ 294 is also not divisible by 9.

4. 432
Answer:
Given number = 432
∵ Sum of the digits = 4 + 3 + 2 = 9 9 is divisible by 9.
∴ 432 is also divisible by 9.

5. 927
Answer:
Given number = 927
∵ Sum of the digits = 9 + 2 + 7 = 18 18 is divisible by 3.
∴ 927 is also divisible by 3.