RBSE Solutions for Class 8 Maths Chapter 16 संख्याओं के साथ खेलना Ex 16.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 16 संख्याओं के साथ खेलना Ex 16.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 16 संख्याओं के साथ खेलना Ex 16.1

निम्नलिखित में से प्रत्येक में अक्षरों के मान ज्ञात कीजिए तथा संबद्ध चरणों के लिए कारण भी दीजिए.

प्रश्न 1.

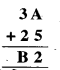
हल:
यहाँ दो अक्षर हैं जिनका मान ज्ञात करना है। इकाई के खाने में योग को देखें, अर्थात् A+5 से हम प्राप्त करते हैं 2, अर्थात् वह संख्या जिसका इकाई अंक 2 है। यह होने के लिए, A का 7 होना जरूरी है (∵ A + 5 = 7+ 5 = 12)
अतः दहाई के खाने में योग के लिए, हमारे पास है 1 + 3 + 2 = B या B = 6 
अतः, हल होगा

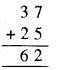
∴ A और B के मान क्रमशः 7 और 6 हैं।

प्रश्न 2.

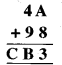
हल:
यहाँ 3 अक्षर हैं जिनका मान ज्ञात करना है। इकाई के खाने में योग को देखें, अर्थात् A + 8 से हम प्राप्त करते हैं 3, अर्थात् वह संख्या जिसका इकाई अंक 3 है। यह होने के लिए Á का मान 5 होना जरूरी है (∵ A + 8 = 5 + 8 = 13) 
अतः, दहाई के खाने में योग के लिए हमारे पास है। 1 + 4 + 9 = B या 14 = B
∴ स्पष्ट है, B, 4 है और C, 1 है। 
अतः, पहेली का हल होगा

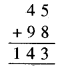
∴ A, B और C के सम्भावित मान क्रमशः 5, 4 और 1 होंगे।

प्रश्न 3.

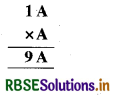
हल:
चूँकि A × A का इकाई अंक A है, अतः A = 1 या A = 5 या A = 6 होना जरूरी है।
जब A = 1, तब

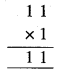
अतः, हमें A = 1 नहीं मिल सकता।

जब = 5, तब .. 15

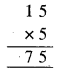
अतः, हमें A = 5 भी नहीं मिल सकता।

जब = 6, तब

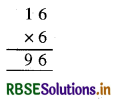
अतः, A = 6 चुनाव ठीक काम करता है। 
अतः A = 6

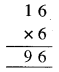
प्रश्न 4.

हल:
यहाँ दो अक्षरों के सम्भावित मान ज्ञात करने हैं, वे हैं-A और B दी गई पहेली में योग का अध्ययन करें। अर्थात् B + 7 से हमें A मिलता है और A + 3 से 6 सम्भावित मान हो सकता है। 0 + 7 = 7. अर्थात् A = 7 लेकिन 7 + 3 ≠ 6,
अतः, अस्वीकार्य 1 + 7 = 8 अर्थात् A = 8 लेकिन 8 + 3 ≠ 6,
अतः, अस्वीकार्य 2 + 7 = 9 अर्थात् A = 9 लेकिन 9 + 3 ≠ 6,
अतः, अस्वीकार्य 3 + 7 = 10 अर्थात् A = 0 लेकिन 1 + 0 + 3 ≠ 6,
अतः, अस्वीकार्य 4 + 7 = 11 अर्थात् A = 1 लेकिन 1 + 1 + 3 ≠ 6,
अतः, अस्वीकार्य 5 + 7 = 12 अर्थात् A = 2 लेकिन 1 + 2 + 3 = 6 
अतः, B = 5, यह मान ठीक से काम करता है और B = 5 से A, 2 के रूप में प्राप्त होता है। अतः, पहेली का हल होगा

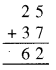
∴ A = 2 और B = 5 

प्रश्न 5.

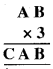
हल:
इसमें तीन अक्षर हैं, जिनका मान ज्ञात करना है A, B और C 
चूँकि 3 × B का इकाई अंक B है, तो यह जरूर ही B = 0 होना चाहिए। अतः पहले होगी

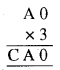
चूँकि 3 × A का इकाई अंक A है, इसलिए A = 5 होगा। , अतः, पहेली का हल होगा

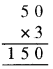
∴ A = 5, B = 0 और C = 1

प्रश्न 6.

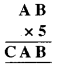
हल:
इसमें तीन अक्षर हैं जिनका मान ज्ञात करना है : A, B और C 
चूँकि 5 × B का इकाई अंक B है, इसलिए B = 0 या B = 5 होना चाहिए। 
यदि B = 0, तब पहेली होगी

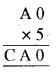
अब, 5 × A = A= A = 0 या 5
लेकिन A ≠ 0 चूँकि उत्तर में एक तीसरा अक्षर भी है।
A = 5 के लिए, पहेली होगी ।

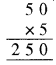
∴ A = 5, B = 0 और C = 2 
यदि B = 5, तब पहेली होगी

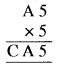
अब, 5 × A = 2 = 2 ⇒ A = 2, 5 × 2 + 2 = 12 के रूप में, अतः, इकाई अंक 2 है जो A के बराबर है।

∴ B = 5 के लिए, पहेली का हल होगा

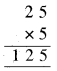
∴ A = 2, B = 5 और C = 1 

प्रश्न 7.

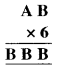
हल:
इसमें दो अक्षरों का मान ज्ञात करना है : A और B

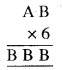
BBB के सम्भावित मान 111, 222, 333, .... इत्यादि हैं।
आइए इन संख्याओं का 6 से विभाजन करें। 111 ÷ 6 = 18, शेषफल 3, अत: 111 अस्वीकार है। 222 ÷ 6 = 37, शेषफल 0, अतः भागफल 37, A2 के रूप में है। 
इस प्रकार 222 अस्वीकार है। 333 ÷ 6 = 55, शेषफल 3, अत: 333 अस्वीकार है। 
444 ÷ 6 = 74, शेषफल 4, भागफल 74, A4 के रूप में है। अतः, पहेली का हल होगा

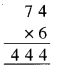
अतः, उत्तर है A = 7 और B = 4

प्रश्न 8.

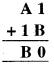
हल:
इसमें दो अक्षर हैं जिनका मान ज्ञात करना है ; A और
इकाई के खाने में योग का अध्ययन करें : 1 + B से हम 0 प्राप्त करते हैं, जो वह संख्या है जिसका इकाई अंक 0 है। यह होने के लिए, B का दहाई अंक 9 होना चाहिए और चूँकि B स्वयं एक अंक है, हमें प्राप्त होता है B = 9, अतः पहेली होगी

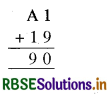
लेकिन 90 - 19 = 71, अत: A1 = 71 
⇒ A = 7 इस प्रकार, A = 7 और B = 9

प्रश्न 9.

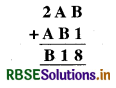
हल:
दो अक्षरों का मान ज्ञात करना है : A और B इकाई के खाने में योग को देखिए, अर्थात् B+ 1 से हम प्राप्त करते हैं 8, जो वह संख्या है जिसका इकाई अंक 8 है। यह होने के लिए, B का इकाई अंक 7 होना चाहिए। चूँकि B स्वयं एक अंक है, हम प्राप्त करते हैं B= 7, अतः पहेली होगी

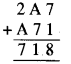
अतः, योग को दहाई के खाने में देखें, अर्थात् A+7 से, हम प्राप्त करते हैं 1, जो वह संख्या है जिसका इकाई अंक 1
यह होने के लिए, A का इकाई अंक 4 होना चाहिए। चूंकि A स्वयं एक अंक है, हम पाते हैं A = 4, अतः पहेली का हल होगा

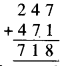
अतएव, A और B के सम्भावित मान क्रमशः 4 और 7 होंगे। 

प्रश्न 10.

हल:
इसमें दो अक्षर हैं, जिनका सम्भावित मान ज्ञात करना है : A और B दहाई के खाने में योग की जाँच करें : 2 + A से हम पाते हैं 0, यह वह संख्या है जिसका इकाई अंक 0 है। यह होने के लिए, A का इकाई अंक 8 होना चाहिए और चूँकि A स्वयं एक अंक है, अतः हमें प्राप्त होगा A = 8, अतः पहेली होगी

अब, इकाई के खाने में योग को देखें : 8 + B से हम प्राप्त करते हैं 9; यह होने के लिए, हमारे पास B = 1 होना चाहिए। अतः पहेली का हल होगा

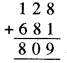
∴ A = 8 और B = 1