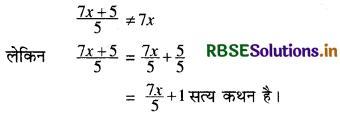RBSE Solutions for Class 8 Maths Chapter 14 गुणनखंडन Ex 14.4

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 14 गुणनखंडन Ex 14.4 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 14 गुणनखंडन Ex 14.4

निम्नलिखित गणितीय कथनों में त्रुटि ज्ञात करके उसे सही कीजिए

प्रश्न 1.
4(x - 5) = 4x - 5
हल:
बायाँ पक्ष = 4(x - 5) = 4 × x - 4 × 5
= 4x - 20
∴ दायाँ पक्ष होना चाहिए = 4x - 20
अतः 4(x -5) = 4x - 20 सही कथन है।

प्रश्न 2.
x(3x + 2) = 3x² + 2
हल:
बायाँ पक्ष = x(3x + 2) = x × 3x + x × 2
= 3x² + 2x
∴ दायाँ पक्ष होना चाहिए = 3x² + 2x
अतः, (3x + 2) = 3x² + 2x सही कथन है।

प्रश्न 3.
2x + 3y = 5xy
हल:
कथन 2x + 3y = 5ry गलत है।
ऐसे पदों को केवल साथ में समूहित किया जा सकता है।
अतएव, 2x + 3y = 2x + 3y सत्य कथन है।

प्रश्न 4.
x + 2x + 3x = 5x
हल:
योग पर गुणन की वितरणशील राशि का प्रयोग करने पर,
x + 2x + 3x = (1 + 2 + 3)x = 6x
इस प्रकार, x + 2x + 3x ≠ 5x, लेकिन x + 2x + 3x = 6x सत्य कथन है।

प्रश्न 5.
5y + 2y + y - 7y = 0
हल:
योग पर गुणन की वितरणशील राशि का प्रयोग करने पर,
5y + 2y + y - 7y = (5 + 2 + 1 - 7)y
= (8 - 7)y = y
इस प्रकार, 5y + 2 + y - 7y ≠ 0, लेकिन 5y + 2y + y - 7y = y सत्य कथन है।

प्रश्न 6.
3x + 2x = 5x²
हल:
योग पर गुणन की वितरणशील राशि का प्रयोग करने पर,
3x + 2x = (3 + 2)x = 5x
इस प्रकार, 3x + 2x ≠ 5x², लेकिन 3x + 2x = 5x सत्य कथन है।

प्रश्न 7.
(2x)² + 4(2x) + 7 = 2x² + 8x + 7
हल:
बायाँ पक्ष = (2x)² + 4(2x) +7
= 2x × 2x + 4 × 2x + 7
= 4x² + 8x + 7
इस प्रकार, (2x)² + 4(2x) + 7 ≠ 2x² + 8x + 7, लेकिन
(2x)² + 4(2x) + 7 = 4x² + 8x + 7 सही कथन है।

प्रश्न 8.
(2x)² + 5x = 4x + 5x = 9x
हल:
चूँकि (2x)² = 2x × 2x = 4x²
∴ (2x) + 5x = 4x + 5x
इस प्रकार, (2x)² + 5x ≠ 4x + 5x = 9x लेकिन
(2x)² + 5x = 4x² + 5x
सही कथन है। साथ ही, 4x² + 5x ≠ 9x

प्रश्न 9.
(3x + 2)² = 3x² + 6x + 4
हल:
बायाँ पक्ष = (3x + 2)² = (3x)² + 2 × 3x × 2 + 2²
= 9x² + 12x + 4
इस प्रकार, (3x + 2)² ≠ 3x² + 6x + 4, लेकिन
(3x + 2)² = 9x² + 12x + 4 सही कथन है।

प्रश्न 10.
x = -3 प्रतिस्थापित करने पर प्राप्त होता है।
(a) x² + 5x + 4 से (- 3)² + 5(- 3) + 4 = 9 + 2 + 4 = 15 प्राप्त होता है।
(b) x² - 5x + 4 से (- 3)² - 5(- 3) + 4 = 9 - 15 + 4 = -2 प्राप्त होता है।
(c) x² + 5x से (-3) + 5(- 3) = - 9 - 15 = - 24 प्राप्त होता है।
हल:
(a) x = - 3 प्रतिस्थापित करने पर, x² + 5x + 4,
x² + 5x + 4 = (- 3)² + 5(-3) + 4
= - 3 × - 3 + 5 × - 3 + 4
= 9 - 15 + 4 = 13 - 15 = - 2.
इस प्रकार, x = - 3 के लिए, x² + 5x + ≠ 15, लेकिन
यह - 2 के समतुल्य है।

(b) x = - 3 प्रतिस्थापित करने पर x² - 5x + 4,
x² - 5x + 4 = (-3)² - 5(-3) + 4
= - 3 × - 3 - 5 × - 3 + 4
= 9 + 15 + 4 = 28
इस प्रकार, x = - 3 के लिए, x² - 5x + 4 ≠ - 2, लेकिन यह 28. के समतुल्य है।

(c) x = -3 प्रतिस्थापित करने पर x² + 5x
x² + 5x = (-3)² + 5(- 3)
= 9 - 15 = - 6
इस प्रकार, x = - 3 के लिए, x² + 5x ≠ - 24, लेकिन यह -6 के समतुल्य है।

प्रश्न 11.
(y - 3)² = y² - 9
हल:
बायाँ पक्ष = (y - 3)² = y² - 2 × y × 3 + (-3)²
= y² - 6y + 9
इस प्रकार, (y - 3)² ≠ y - 9, लेकिन (y - 3)² = y² - 6y + 9 सत्य कथन है।

प्रश्न 12.
(z + 5)² = z² + 25
हल:
बायाँ पक्ष = (z + 5)² = z² + 2 × z × 5 + 5²
= z² + 10z + 25
इस प्रकार (z + 5)² ≠ z² + 25, लेकिन (z + 5)² = z² + 10z + 25 सत्य कथन है।

प्रश्न 13.
(2a + 3b)(a - b) = 2a² - 3b²
हल:
बायाँ पक्ष = (2a + 3b)(a - b)
= 2a(a - b) + 3b(a - b)
= 2a × a - 2a × b + 3b × a - 3b × b
= 2a² - 2ab+ 3ab - 3b²
= 2a² + ab - 3b²
इस प्रकार, (2a + 3b)(a - b) ≠ 2a² - 3b², लेकिन (2a + 3b) (a - b) = 2a² + ab - 3b² सत्य कथन है।

प्रश्न 14.
(a + 4)(a + 2) = a² + 8
हल:
बायाँ पक्ष = (a + 4)(a + 2)
= a² + (4 + 2) a + 4 × 2
= a² + 6a + 8
इस प्रकार, (a + 4)(a + 2) ≠ a² + 8, लेकिन (a + 4)(a + 2) = a² + 6a + 8 सत्य कथन है।

प्रश्न 15.
(a - 4)(a - 2) = a² - 8
हल:
बायाँ पक्ष = (a - 4) (a - 2)
= a² - (4 + 2)a + (-4 × - 2)
= a² - 6a + 8
इस प्रकार, (a - 4) (a - 2) ≠ a² - 8, लेकिन (a - 4)(a - 2) = a² - 6a + 8 सत्य कथन है।

प्रश्न 16.
\(\frac{3 x^{2}}{3 x^{2}}\) = 0
हल:
बायाँ पक्ष = \(\frac{3 x^{2}}{3 x^{2}}\) = 1
इस प्रकार, \(\frac{3 x^{2}}{3 x^{2}}\) ≠ 0, लेकिन \(\frac{3 x^{2}}{3 x^{2}}\) ≠ 1 सत्य कथन है। |

प्रश्न 17.
\(\frac{3 x^{2}+1}{3 x^{2}}\) = 1 + 1 = 2
हल:

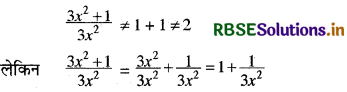
प्रश्न 18.
\(\frac{3 x}{3 x+2}\) = \(\frac{1}{2}\)
हल:
\(\frac{3 x}{3 x+2}\) ≠ \(\frac{1}{2}\)
लेकिन \(\frac{3 x}{3 x+2}\) = \(\frac{3 x}{3 x+2}\) सत्य कथन है।

प्रश्न 19.
\(\frac{3}{4 x+3}\) = \(\frac{1}{4 x}\)
हल:
\(\frac{3}{4 x+3}\) ≠ \(\frac{1}{4 x}\)
लेकिन \(\frac{3}{4 x+3}\) = \(\frac{3}{4 x+3}\) सत्य कथन है।

प्रश्न 20.
\(\frac{4 x+5}{4 x}\) = 5
हल:
\(\frac{4 x+5}{4 x}\) ≠ 5
लेकिन \(\frac{4 x+5}{4 x}=\frac{4 x}{4 x}+\frac{5}{4 x}=1+\frac{5}{4 x}\) सत्य कथन है। उत्तर

प्रश्न 21.
\(\frac{7 x+5}{5}\) = 7x
हल: