RBSE Solutions for Class 8 Maths Chapter 14 गुणनखंडन Ex 14.3

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 14 गुणनखंडन Ex 14.3 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 14 गुणनखंडन Ex 14.3

प्रश्न 1.
निम्नलिखित विभाजन कीजिए
(i) 28x⁴ ÷ 56x
हल:

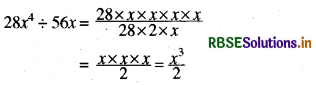
(ii) - 36y³ ÷ 9y²
हल:

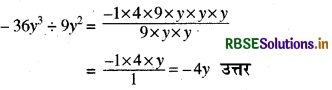
(iii) 66pq²r³ ÷ 11qr²
हल:

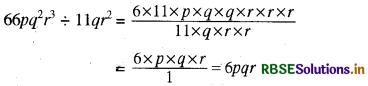
(iv) 34x³y³z³÷ 51xy²z³
हल:
34x³y³z³÷ 51xy²z³

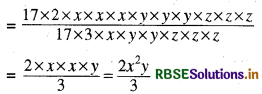
(v) 12a⁸b⁸ ÷ (-6a⁶b⁴)
हल:
12a⁸b⁸ ÷ (-6a⁶b⁴)

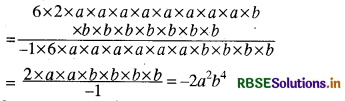
प्रश्न 2.
दिए हुए बहुपद को दिए हुए एकपदी से भाग दीजिए
(i) (5x² - 6x) ÷ 3x
हल:

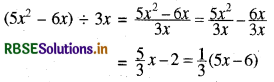
(ii) (3y⁸ - 4y⁶ + 5y⁴) ÷ y⁴
हल:

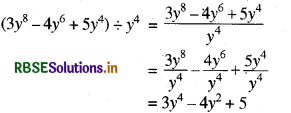
(iii) 8(x³y²z² + x²y³z²+ x²y²z²) ÷ 4x²y²z²
हल:

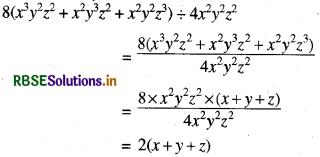
(iv) (x³ + 2x² + 3x) ÷ 2x
हल:

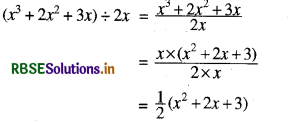
(v) (p³q⁶ - p⁶q³) ÷ p³q³
हल:

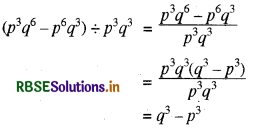
प्रश्न 3.
निम्नलिखित विभाजन कीजिए
(i) (10x - 25) ÷ 5
हल:

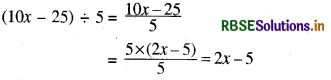
(ii) (10x - 25) ÷ (2x - 5)
हल:
(10x - 25) ÷ (2x - 5) = \(\frac{5 \times(2 x-5)}{(2 x-5)}\) = 5

(iii) 10y(6y + 21) ÷ 5(2y + 7)
हल:

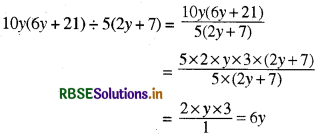
(iv) 9x²y2 (3z - 24) ÷ 27xy(z - 8)
हल:

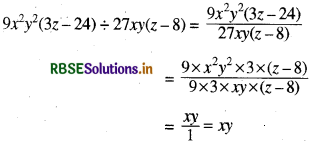
(v) 96abc(3a - 12) (5b - 30) ÷ 144(a - 4) (b - 6)
हल:
96abc(3a - 12) (5b - 30) ÷ 144(a - 4) (b - 6)

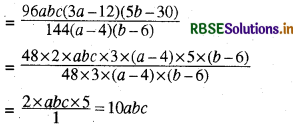
प्रश्न 4.
निर्देशानुसार भाग दीजिए
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1)
हल:
5(2x + 1) (3x + 5) ÷ (2x + 1)

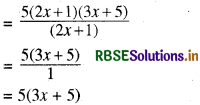
(ii) 26xy(x + 5) (y - 4) ÷ 13x(y - 4)
हल:
26xy(x + 5) (y - 4) ÷ 13x(y - 4)

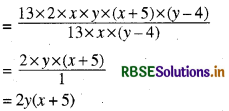
(iii) 52pqr(p + q) (q + r) (r + p) ÷ 104pq(q + r) (r + p)
हल:
52pqr(p + q) (q + r) (r + p) ÷ 104pq(q + r) (r + p)

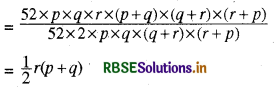
(iv) 20(y + 4) (y² + 5y + 3) ÷ 5(y + 4)
हल:
20(y + 4) (y² + 5y + 3) ÷ 5(y + 4)

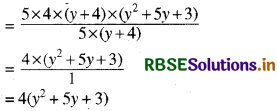
(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
हल:
x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)

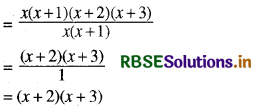
प्रश्न 5.
व्यंजक के गुणनखंड कीजिए और निर्देशानुसार भाग दीजिए
(i) (y² + 7y + 10) ÷ (y + 5)
हल:
प्रश्नानुसार
(y² + 7y + 10) = y² + 2y + 5y + 10
= y(y + 2) + 5(y + 2)
= (y + 2) (y +5) .....(1)
(y² + 2)(y + 5)
अतः (y² + 7y + 10) ÷ (y + 5) = \(\frac{(y+2)(y+5)}{y+5}\) [(1) का प्रयोग करने पर]
= y + 2

(ii) (m² - 14m - 32) ÷ (m+2)
हल:
(m² - 14m - 32) = m² + 2m - 16m - 32
= m(m + 2) - 16(m + 2)
= (m + 2)(m - 16) ...... (1)
अतः (m² - 14m - 32) ÷ (m + 2) = \(\frac{(m+2)(m-16)}{m+2}\)
[(1) का प्रयोग करने पर]
= m - 16

(iii) (5p² - 25p + 20) ÷ (p - 1)
हल:
प्रश्नानुसार 5p² - 25p + 20 = 5(p² - 5p + 4)
= 5(p² - p - 4p + 4)
= 5[p(p - 1) - 4(p - 1)]
= 5(p - 1)(p - 4) ....... (1)
अतः (5p² - 25p + 20) ÷ (p - 1) = \(\frac{5 p^{2}-25 p+20}{p-1}\)
= \(\frac{5(p-1)(p-4)}{p-1}\)
[(1) का प्रयोग करने पर]
= 5(p - 4)

(iv) 4yz(z² + 6 - 16) ÷ 2y(z + 8)
हल:
प्रश्नानुसार 4yz(z² + 6z - 16) = 4yz(z² + 8z - 2z - 16)
= 4yz[z(z + 8) - 2(z + 8)]
= 4yz(z + 8)(z - 2) ....... (1)
अत: 4yz(z² + 6z - 16) ÷ 2y(z + 8)
= \(\frac{4 y z\left(z^{2}+6 z-16\right)}{2 y(z+8)}\)
= \(\frac{4 y z(z+8)(z-2)}{2 y(z+8)}\) [(1) का प्रयोग करने पर]
= \(\frac{2 z(z-2)}{1}\) = 2z(4 - 2)

(v) 5pq(p² - q²) ÷ 2p(p + q)
हल:
प्रश्नानुसार 5pq(p² - q²) = 5pq(p - q)(p + q)
अतः 5pq(p² - q²) ÷ 2p(p+ q) = \(\frac{5 p q\left(p^{2}-q^{2}\right)}{2 p(p+q)}\)
= \(\frac{5 \times p \times q \times(p-q) \times(p+q)}{2 \times p \times(p+q)}\)
[(1) का प्रयोग करने पर]
= \(\frac{5}{2}\)q(p - q)

(vi) 12xy(9x² - 16y²) ÷ 4xy(3x + 4y)
हल:
प्रश्नानुसार 9x² - 16y² = (3x)² - (4y)²
= (3x + 4y)(3x - 4y) ....... (1)
अतः 12xy(9x² - 16y²) ÷ 4xy(3x + 4y)
= \(\frac{12 x y(3x + 4 y)(3 x - 4 y)}{4 x y(3 x+4 y)}\)
[(1) का प्रयोग करने पर]
= 3(3x - 4y)

(vii) 39y³3(50y² - 98) ÷ 26y² (5y + 7)
हल:
प्रश्नानुसार 39y³(50y² - 98) = 39y³ × 2 × (25y² - 49)
= 78y³ × [(5y)² - 7²]
= 78y³ × (5y - 7)(5y + 7) ...... (1)
अत: 39y³(50y³ - 98) ÷ 26y² (5y + 7)
= \(\frac{78 y^{3}(5 y-7)(5 y+7)}{26 y^{2}(5 y+7)}\)
[समी. (1) का प्रयोग करने पर]
= 3.y(5y - 7)