RBSE Solutions for Class 8 Maths Chapter 14 Factorization Ex 14.3

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 14 Factorization Ex 14.3 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 14 Factorization Ex 14.3

Question 1.
Carry out the following divisions:
(i) 28x⁴ ÷ 56x
Answer:
28x⁴ ÷ 56x = $\frac{28 \times x \times x \times x \times x}{28 \times 2 \times x}$
= $\frac{x \times x \times x}{2}=\frac{x^{3}}{2}$

(ii) - 36y³ ÷ 9y²
Answer:
- 36y³ ÷ 9y² = $\frac{-1 \times 4 \times 9 \times y \times y \times y}{9 \times y \times y}$
= $\frac{-1 \times 4 \times y}{1}$ = -4y

(iii) 66pq²r³ ÷ 11qr²
Answer:
= $\frac{6 \times 11 \times p \times q \times q \times r \times r \times r}{11 \times q \times r \times r}$
= $\frac{6 \times p \times q \times r}{1}$ = 6pqr

(iv) 34x³y³z³ ÷ 51xy²z³
Answer:
= $\frac{17 \times 2 \times x \times x \times x \times y \times y \times y \times z \times z \times z}{17 \times 3 \times x \times y \times y \times z \times z \times z}$
= $\frac{2 \times x \times x \times y}{3}=\frac{2 x^{2} y}{3}$

(v) 12a⁸b⁸ ÷ (- 6a⁶b⁴)
Answer:

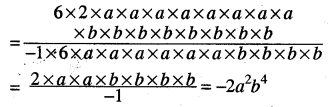
Question 2.
Divide the given polynomial by the given monomial:
(i) (5x² - 6x) ÷ 3x
Answer:
(5x² - 6x) ÷ 3x = $\frac{5 x^{2}-6 x}{3 x}=\frac{5 x^{2}}{3 x}-\frac{6 x}{3 x}$
= $\frac{5}{3} x - 2 = \frac{1}{3}(5x - 6)$

(ii) (3y⁸ - 4y⁶ + 5y⁴) ÷ y⁴
Answer:
= $\frac{5}{3}$ x - 2 = $\frac{1}{3}$
= $\frac{3 y^{8}}{y^{4}}-\frac{4 y^{6}}{y^{4}}+\frac{5 y^{4}}{y^{4}}$
= 3y⁴ - 4y² + 5

(iii) 8(x³y²z² + x²y³z² + x²y²z³) ÷ 4x²y²z²
Answer:
= $\frac{8\left(x^{3} y^{2} z^{2}+x^{2} y^{3} z^{2}+x^{2} y^{2} z^{3}\right)}{4 x^{2} y^{2} z^{2}}$
= $\frac{8 \times x^{2} y^{2} z^{2} \times(x+y+z)}{4 x^{2} y^{2} z^{2}}$
= 2(x + y + z)

(iv) (x³ + 2x² + 3x) ÷ 2x
Answer:
= $\frac{x^{3}+2 x^{2}+3 x}{2 x}$
= $\frac{x \times\left(x^{2}+2 x+3\right)}{2 \times x}$
= $\frac{1}{2}$(x² + 2x + 3)

(v) (p³q⁶ - p⁶q³) ÷ p³q³
Answer:
= $\frac{p^{3} q^{6}-p^{6} q^{3}}{p^{3} q^{3}}$
= $\frac{p^{3} q^{3}\left(q^{3}-p^{3}\right)}{p^{3} q^{3}}$
= q³ - p³

Question 3.
Workout the following divisions:
(i) (10x - 25) ÷ 5
Answer:
(10x - 25) ÷ 5 = $\frac{10 x-25}{5}$
= $\frac{5 \times(2 x-5)}{5}$
= 2x - 5

(ii) (10x - 25) ÷ (2x - 5)
Answer:
(10x - 25) ÷ (2x - 5) = $\frac{5 \times(2 x-5)}{(2 x-5)}$ = 5

(iii) 10y(6y + 21) ÷ 5(2y + 7)
Answer:
= $\frac{10 y(6 y+21)}{5(2 y+7)}$
= $\frac{5 \times 2 \times y \times 3 \times(2 y+7)}{5 \times(2 y+7)}$
= $\frac{2 \times y \times 3}{1}$ = 6y

(iv) 9x²y²(3z - 24) ÷ 27xy(z - 8)
Answer:
= $\frac{9 x^{2} y^{2}(3 z-24)}{27 x y(z-8)}$
= $\frac{9 \times x^{2} y^{2} \times 3 \times(z-8)}{9 \times 3 \times x y \times(z-8)}$
= $\frac{x y}{1}$ = xy

(v) 9oabc(3a - 12)(5b - 30) ÷ 144(a - 4)(b - 6)
Answer:
= $\frac{96 a b c(3 a-12)(5 b-30)}{144(a-4)(b-6)}$
= $\frac{48 \times 2 \times a b c \times 3 \times(a-4) \times 5 \times(b-6)}{48 \times 3 \times(a-4) \times(b-6)}$
= $\frac{2 \times a b c \times 5}{1}$ = 10abc

Question 4.
Divide as directed:
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1)
Answer:
5(2x + 1) (3x + 5) ÷ (2x + 1) = $\frac{5(2 x+1)(3 x+5)}{(2 x+1)}$
= $\frac{5(3 x+5)}{1}$
= 5(3x + 5)

(ii) 26xy(x + 5) (y - 4) ÷ 13x(y - 4)
Answer:
= $\frac{13 \times 2 \times x \times y \times(x+5) \times(y-4)}{13 \times x \times(y-4)}$
= $\frac{2 \times y \times(x+5)}{1}$
= 2y(x + 5)

(iii) 51pqr(p + q) (q + r) (r + p) ÷ 104pq (q + r) (r + p)
Answer:
= $\frac{52 \times p \times q \times r \times(p+q) \times(q+r) \times(r+p)}{52 \times 2 \times p \times q \times(q+r) \times(r+p)}$
= $\frac{1}{2}$r(p + q)

(iv) 20(y + 4) (y² + 5y + 3) ÷ 5(y + 4)
Answer:
= $\frac{5 \times 4 \times(y+4) \times\left(y^{2}+5 y+3\right)}{5 \times(y+4)}$
= $\frac{4 \times\left(y^{2}+5 y+3\right)}{1}$
= 4(y² +5y + 3)

(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
Answer:
= $\frac{x(x+1)(x+2)(x+3)}{x(x+1)}$
= $\frac{(x+2)(x+3)}{1}$
= (x + 2)(x + 3)

Question 5.
Factorise the expressions and divide them as directed:
(i) (y² + 7y + 10) ÷ (y + 5)
Answer:
We have,
(y² + 7y + 10) = y² + 2y + 5y + 10
= y(y + 2) + 5(y + 2)
= (y + 2) (y + 5) ...............(1)
(y² + 7y + 10) ÷ (y + 5) = $\frac{(y+2)(y+5)}{y+5}$ [Using (1)]
= y + 2

(ii) (m² - 14m - 32) ÷ (m + 2)
Answer:
We have,
(m² - 14m - 32) = m² + 2m - 16m - 32
= m(m + 2) - 16(m + 2)
= (m + 2)(m - 16) ....(1)
(m² - 14m - 32) ÷ (m + 2) = $\frac{(m+2)(m-16)}{m+2}$ [Using (1)]
= m - 16

(iii) (5p² - 25p + 20) ÷ (p - 1)
Answer:
We have,
5p² - 25p + 20 = 5(p² - 5p + 4)
= 5(p² - p - 4p + 4)
= 5(p - 1) - 4(p- 1)]
= 5(p - 1)(p - 4) ................. (1)
(5p² - 25p + 20) ÷ (p - 1)
= $\frac{5 p^{2}-25 p+20}{p-1}$
= $\frac{5(p-1)(p-4)}{p-1}$
= 5(p - 4) [Using (1)]
= 5(p - 4)

(iv) 4yz(z² + 6z - 16) ÷ 2y(z + 8)
Answer:
We have,
4yz(z² + 6z - 16) = 4yz(z² + 8z - 2z - 16)
= 4yz[z(z + 8) -2(z + 8)]
= 4yz(z.+8)(z - 2) ..........(1)

4yz(z² + 6z - 16) ÷ 2y(z + 8)
= $\frac{4 y z\left(z^{2}+6 z-16\right)}{2 y(z+8)}$
= $\frac{4 y z(z+8)(z-2)}{2 y(z+8)}$ [Using (1)]
= $\frac{2 z(z-2)}{1}$ = 2z(z - 2)

(v) 5pq(p² - q²) ÷ 2p(p + q)
Answer:
We have,
5pq(p² - q²) = 5pq(p - q)(p + q)
5pq(p² - q²) ÷ 2p(p + q) = $\frac{5 p q\left(p^{2}-q^{2}\right)}{2 p(p+q)}$
= $\frac{5 \times p \times q \times(p-q) \times(p+q)}{2 \times p \times(p+q)}$ [Using (1)]
= $\frac{5}{2}$q(p - q)

(vi) 12xy(9x² - 16y²) ÷ 4xy(3x + 4y)
Answer:
We have,
9x² - 16y² = (3x)² - (4y)²
= (3x + 4y)(3x - 4y) ................. (1)
12xy(9x² - 16y²) ÷ 4xy(3x + 4y) = $\frac{12 x y(3 x+4 y)(3 x-4 y)}{4 x y(3 x+4 y)}$ [Using (1)]
= 3(3x - 4y)

(vii) 39y³(50y² - 98) ÷ 26y²(5y + 7)
Answer:
We have,
39y³(50y² - 98) = 39y³ x 2 x (25y² - 49)
= 78y³ x [(5y)²³ - 7²]
= 78y³ x (5y - 7)(5y + 1) .........(1)
∴ 39y³(50y² - 98) ÷ 26y²(5y + 7)
= $\frac{78 y^{3}(5 y-7)(5 y+7)}{26 y^{2}(5 y+7)}$ [Using (1)]
= 3y(5y - 7)