RBSE Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 13 Direct and Inverse Proportions Intext Questions

(Page 201)

Question 1.
Mohan prepares tea for himself and his sister. He uses 300 mL of water, 2 spoons of sugar, 1 spoon of tea leaves and §0 mL of milk. How much quantity of each item will he need, if he has to make tea for five persons?
Answer:
For 2 persons, water needed
= 300 mL
For 5 persons, water needed = \(\frac{300}{2}\) × 5mL
= 750 mL
For 2 persons, sugar needed = 2 spoons
For 5 persons, sugar needed = \(\frac{2}{2}\) × 5
= 5 spoons
For 2 persons, tea leaves needed = 1 spoon
∴ For 5 persons, tea leaves needed
= \(\frac{1}{2}\) × 5 = 2\(\frac{2}{2}\) spoons
For 2 perons, milk needed = 50 mL
∴ For 5 persons, milk needed
= \(\frac{50}{2}\) × 5 mL = 125 mL
Hence, Mohan needs 750 mL of water, 5
spoons of sugar, 2\(\frac{2}{2}\) spoons of tea leaves and 125 mL of milk to make tea for 5 persons.

Question 2.
If two students take 20 minutes to arrange chairs for an assembly, then how much time would five students take to do the same job?
Answer:
Time taken by 2 students to arrange chairs = 20 minutes
Time taken by 1 student to arrange chairs = 20 × 2 = 40 minutes
Time taken by 5 students to arrange chairs
= \(\frac{40}{5}\) minutes
= 8 minutes

(Do This - Page 203)

Question 1.
(i) Take a clock and fix its minute hand at 12.
(ii) Record the angle turned through by the minute hand from its original position and the time that has passed, in the following table :

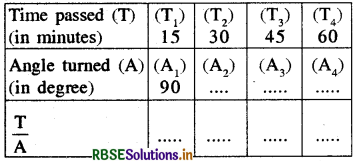
What do you observe about T and A? Do they increase together?
Is \(\frac{T}{A}\) same every time?
Is the angle turned through by the minute hand directly proportional to the time that has passed? Yes.
From the above table, you can also see
T₁ : T₂ = A₁ : A₂, because
T₁ : T₂ = 15: 30 = 1 : 2
A₁ : A₂ = 90 : 180 = 1 : 2
Check if T₂ : T₃ = A₂ : A₃ and T₃ :T₄ = A₃ : A₄
You can repeat this activity by choosing your own time interval.
Answer:

We observed that as T increases, A also increases and \(\frac{T}{A}\) is same every time.
Yes, the angle turned by minute hand is directly proportional to the time that has passed. We also find that
T₂ : T₃ = 30 : 45 = 2 : 3
A₂: A₃ = 180 : 270 = 2 : 3
T₂ : T₃ = A₂ : A₁ = 2 : 3
Also T₃ : T₄ = 45 : 60 = 3 : 4
A₃ : A₄ = 270 : 360 = 3 : 4
∴ T₃ : T₄ = A₃ : A₄ = 3:4

(ii) Do it yourself as this is an activity.

Question 2.
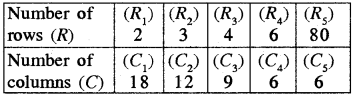
Ask your friend to fill the following table and find the ratio of his age to the corresponding age of his mother.

What do your observe?
Do F and M increase (or decrease) together? Is \(\frac{F}{M}\) same every time? No!
You can repeat this activity with other friends and write down your observations.
Answer:

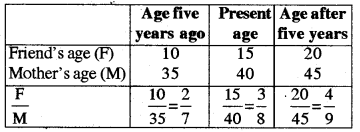
No, F and M do not increase (or decrease) together.
No, \(\frac{F}{M}\) is not same every time.

(Try These - Page 204)

Question 1.
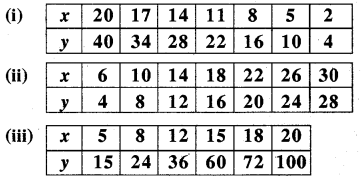
Observe the following tables and find if x and y are directly proportional.

Answer:
(i) We have
\(\frac{20}{40}=\frac{17}{34}=\frac{14}{28}=\frac{11}{22}=\frac{8}{16}=\frac{5}{10}=\frac{2}{4}=\frac{1}{2}\)
Hence, the ratio of the corresponding values of x and y is constant and is equal to \(\frac{1}{2}\). Hence x and y are in direct proportion with, the constant of variation equal to \(\frac{1}{2}\).

(u) We have, \(\frac{6}{4} \neq \frac{10}{8} \neq \frac{14}{12} \neq \frac{18}{16} \neq \frac{22}{20} \neq \frac{26}{24} \neq \frac{30}{28}\)
Thus, the ratio of the corresponding values of x and y is not constant.
Hence x and y are not in direct proportion.

(iii) We have \(\frac{5}{15}=\frac{8}{24}=\frac{12}{36} \neq \frac{15}{60}\) etc.
Thus, the ratio of the corresponding values x and y is not constant.
Hence, x and y are not in direct proportion.

Question 2.
Principal = ₹ 1000, Rate = 8% per annum. Fill in the following table and find which type of interest (simple or compound) changes in direct proportion with time period.

Answer:
Here, P = ₹ 1000, R = 1% p.a.
Simple Interest for 1 year = ₹ \(\left(\frac{1000 \times 8 \times 1}{100}\right)\)
= ₹ 80

Simple Interest for 3 years = ₹ \(\left(\frac{1000 \times 8 \times 3}{100}\right)\)
= ₹ 240

For Compound Interest:
For 1 year : Amount = ₹ 1000\(\left(1+\frac{8}{100}\right)^{1}\)
= ₹ 1000 × \(\frac{108}{100}\)
= ₹ 1080

CI for 1 year = ₹ (1080 - 1000)
= ₹ 80
for 2 years : Amount = ₹ 1000\(\left(1+\frac{8}{100}\right)^{2}\)
= ₹ 1000 × \(\frac{108}{100} \times \frac{108}{100}\)
= ₹ 1166.40

CI for 2 years = ₹ (1166.40 - 1000) = ₹ 166.40
for 3 years : Amount = ₹ 1000\(\left(1+\frac{8}{100}\right)^{3}\)
= ₹ 1000 × \(\frac{108}{100} \times \frac{108}{100} \times \frac{108}{100}\)
= ₹ 1259.712
∴ CI for 3 yeare = ₹ (1259.712 - 1000) = ₹ 259.712
∴ The table becomes :

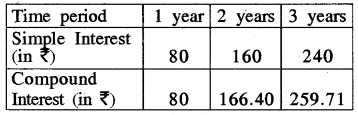
Here \(\frac{S I}{T}=\frac{80}{1}=\frac{160}{2}=\frac{240}{3}\) = 80
So SI is directly proportional to time (T).
Hence it is in direct proportion.

(Do This - Page 208)

Question 1.
On a squared paper, draw five squares of different sides. Write the following information in a tabular form.

Find whether the length of a side is in direct proportion to :
(a) the perimeter of the square.
(b) the area of the square.
Answer:
Square-1 : Let the length of the side (L) = 2 cm
Perimeter (F) = 4 × side
= 4 × 2 = 8 cm
Now, \(\frac{L}{P}=\frac{2}{8}=\frac{1}{4}\)

Square-2 : Let die length of the side (L) = 3 cm
Perimeter (P) = 4 × side
= 4 × 3 = 12 cm
Now, \(\frac{L}{P}=\frac{3}{12}=\frac{1}{4}\)
Area of square (A) = (side)²
= (3)² = 9 cm²
Now, \(\frac{L}{P}=\frac{3}{9}=\frac{1}{3}\)

Square-3 : Let the length of the side (L) = 5 cm
Perimeter (P) = 4 × side = 4 × 5 = 20 cm
Now, \(\frac{L}{P}=\frac{5}{20}=\frac{1}{4}\)
Area of square (A) = (side)²
= (5)² = 25 cm²
Now, \(\frac{L}{P}=\frac{5}{25}=\frac{1}{5}\)

Square-4 : Let the length of the side (L) = 7 cm
Perimeter (P) = 4 × side = 4 × 7 = 28 cm
Now, \(\frac{L}{P}=\frac{7}{28}=\frac{1}{4}\)
Area of square (A) = (side)²
= (7)² = 49 cm²
So, \(\frac{L}{P}=\frac{7}{49}=\frac{1}{7}\)

Square-5 : Let the length of the side (L) = 9 cm
Perimeter (P) = 4 × side = 4 × 9 = 36 cm
Now, \(\frac{L}{P}=\frac{9}{36}=\frac{1}{4}\)
Area of square (A) = (side)²
= (9)² = 81 cm²
So, \(\frac{L}{P}=\frac{9}{81}=\frac{1}{9}\)

By assembling the values in table, we get:

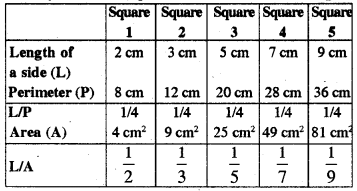
(a) Yes, in table we can see that value of \(\frac{L}{P}\) is same for each square, hence length of side is direct proportion to the perimeter of square.

(b) No, since value of \(\frac{L}{A}\) is different for each square.

Question 2.
The following ingredients are required to make Halwa for 5 persons: Suji/Rawa = 250 g, Sugar = 300 g, Ghee = 200 g, Water = 500 mL.
Using the concept of proportion, estimate the changes in the quantity of ingredients, to prepare Halwa for your class.
Answer:
Ingredients required to make Halwa for 5 persons :
Suji/Raswa = 250 g, Sugar = 300 g, Ghee = 200 g, Water = 500 mL
Let there are 45 students in my class.
∵ If number of person increases, more ingredients are required.
Therefore it is a case of direct variation.
∵ 5 persons : 45 students =1:9
∴ We shall require 9 times of the quantity of ingredients.

Question 3.
Choose a scale and make a map of your classroom, showing windows, doors, blackboard, etc. (An example is given here)

Answer:
It is an activity based question, so do it yourself.

(Think Discuss And Write - Page 209)

Question 1.
Take a few problems discussed so far under ‘direct variation’. Do you think that they can be solved by ‘unitary method’?
Answer:
Let us solve some problems of Exercise 13.1 by ‘unitary method’.
3.
75 mL of base, needs red pigment = 1 part
∴ 1 mL of base, needs red pigment = \(\frac{1}{75}\)part
∴ 1800 mL base, needs red pigment
= \(\frac{1}{75}\) × 1800 parts = 24 parts

4.
In 6 hours, number of bottles filled up = 840
∴ In 1 hour, number of bottles filled up = \(\frac{840}{6}\) = 140
∴ In 5 hour, number of bottles filled up = 140 × 5 = 700 Ans.

10.
In 25 minutes, i.e., \(\frac{25}{60}\)hours, distance travelled = 14 km
∴ In 1 hour, distance travelled
= 14 ÷ \(\frac{25}{60}\) = (14 × \(\frac{60}{25}\))km

∴ In 5 hours, distance travelled
= (14 × \(\frac{60}{25}\) × 5)km
= 168km

(Do this - Page 211)

Question 1.
Take a squared paper and arrange 48 counters on it in different number of rows as shown below :

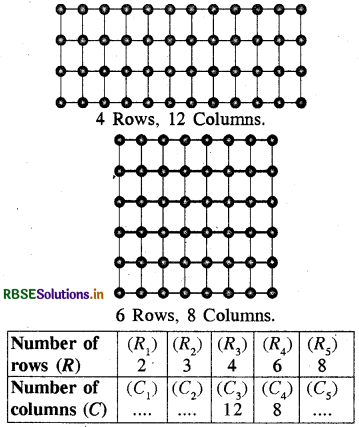
What do you observe? As R increases, C decreases.
(i) Is R₁:R₂ = C₂ :C₁?
(ii) Is R₃ : R₄ = C₄ : C₃?
(iii) Are R and C inversely proportional to each other?
Try this activity with 36 counters.
Answer:
For 2 rows there will be 24 columns.
For 3 rows there are 16 columns, also for 8 rows there are 6 columns. By putting these values in table we get,

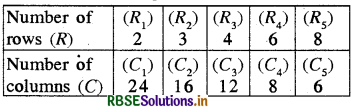
By observing table, we observe that as R increases, C decreases

(iii) By observing table, we see that : R₁C₁ = R₂C₂ = R₃C₃ = R₄C₄ = R₅C₅ = 48
Hence, R and C are inversely proportional to each other.

Let we try this activity for 36 counters.

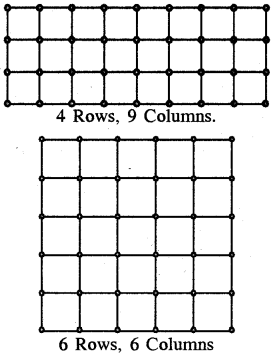
Similarly, for 2 rows there will be 18 columns.
For 3 rows there will be 12 columns.
For 9 rows there will be 4 columns.

Let us arrange these data in a table, we get :

We observe that as R increases, C decreases.

(iii) Yes, R and C inversely proportional to each other.

(Try These - Page 211)

Question 1.
Observe the following tables and And which pair of variables (here x and y) are in Inverse proportion.

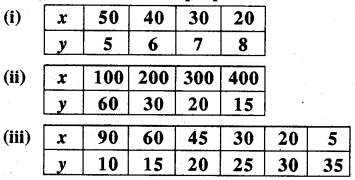
Answer:
(i) We observe that
x × y = 50 × 5 ≠ 40 × 6 ≠ 30 × 7 ≠ 20 × 8
Thus, x and y are not in inverse proportion.

(ii) We observe that
x × y = 100 × 60 = 200 × 30
= 300 × 20 = 400 × 15 = 6000 = constant
Thus, x and y are in inverse proportion.

(iii) We observe that
x × y = 90 × 10 = 60 × 15 = 45 × 20 ≠ 30 × 25 ≠ 20 × 30 ≠ 5 × 35
Thus, x and y are not in inverse proportion.

(Do This - Page 215)

Question 1.
Take a sheet of paper. Fold it as shown in the figure. Count the number of parts and the area of a part in each case.

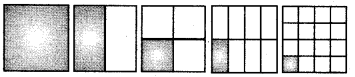
Tabulate your observations and discuss with your friends. Is it a case Inverse proportion? Why?

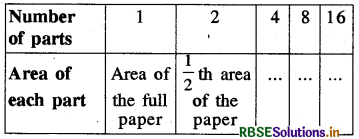
Answer:

Here, more the number of parts, lesser is the area of each part.
∴ It is a case of “inverse proportion”.

Question 2.
Take a few containers of different sizes with circular bases. Fill the same amount of water in each container. Note the diameter of each container and the respective height at which the water level stands. Tabulate your observations. Is it a case of inverse proportion?

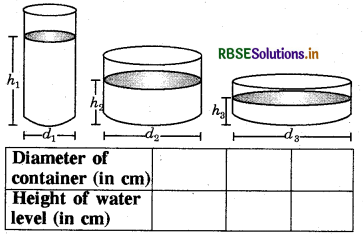
Answer:

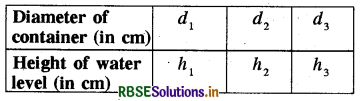
Here, lesser the diameter, more is the level of water in the container.
∴ It is a case of inverse proportion.