RBSE Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions Ex 13.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions Ex 13.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 13 Direct and Inverse Proportions Ex 13.1

Question 1.
Following are the car parking charges near a railway station upto
4 hours ₹ 60
8 hours ₹ 100
12 hours ₹ 140
24 hours ₹ 180
Check if the parking charges are in direct proportion to the parking time.
Answer:
Since \(\frac{4}{60}\) ≠ \(\frac{8}{100}\) ≠ \(\frac{12}{140}\) ≠ \(\frac{24}{180}\)
∴ The parking charges are not in direct proportion to die parking time.

Question 2.
A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added.

Answer:
It is given that part of red pigment, say x and parts of base, say y are in direct proportion. Therefore, the ratio of the corresponding values of x and y remain constant.
We have \(\frac{1}{8}\) = \(\frac{1}{8}\)
So, x and y are in direct variation with the constant of variation equal to \(\frac{1}{8}\). This means that x is \(\frac{1}{8}\)of y and y is 8 times of x. Thus, the required entries are \(\frac{4}{32}\), \(\frac{7}{56}\), \(\frac{12}{96}\), \(\frac{20}{160}\).
Thus table becomes.

Question 3.
In Question 2 above, if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?
Answer:
Let red pigment = x

∵ Parts of red pigment is directly proportional to part of base
∴ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\)
i.e., \(\frac{1}{75}=\frac{x}{1800}\)
⇒ x × 75 = 1 × 1800
⇒ x = \(\frac{1800}{75}\) = 24
Hence, required red pigment = 24

Question 4.
A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Answer:
Let the no. of bottles = x
More the number of hours, more would be the no. of bottles filled. So, the two quantity vary directly.

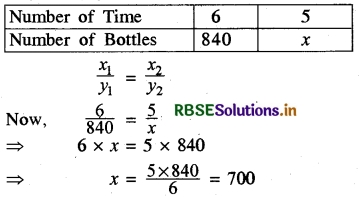
Hence, required bottles = 700

Question 5.
A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?

Answer:
Actual length of bacteria
= \(\frac{5}{50000}\) cm
= \(\frac{1}{50000}\) cm
= \(\frac{1}{10^{4}}\) cm
= 10^-4 cm
Let x be the enlarged length of the bacteria when its photograph is enlarged 20,000 times. Then, we have

Clearly, it is a case of direct variation.
∴ \(\frac{5}{50000}\) = \(\frac{x}{20000}\)
⇒ x = \(\frac{5}{50000}\) × 20000 = 2
Hence, its enlarged length is 2 cm.

Question 6.
In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?

Answer:
We know that more the length of the ship, more would be the length of its mast. So, the two quantity vary directly.

\(\frac{x_{1}}{y_{1}}\) = \(\frac{x_{2}}{y_{2}}\)
⇒ \(\frac{9}{x}\) = \(\frac{12}{28}\)
⇒ x = \(\frac{9 \times 28}{12}\) = 21 cm

Question 7.
Suppose 2 kg of sugar contains 9 × 10⁶ crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?
Answer:
Let x and y crystals are in 5 kg of sugar and 1.2 kg of sugar. Then, we have

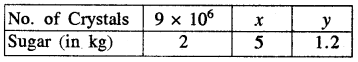
Clearly, it is a case of direct variation

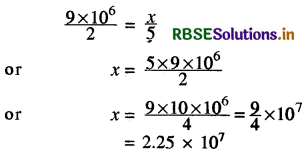
Hence, 5 kg of sugar contains 2.25 × 10⁷ crystals.

(ii)
\(\frac{9 \times 10^{6}}{2}\) = \(\frac{y}{1.2}\)
or y = \(\frac{1.2 \times 9 \times 10^{6}}{2}\)
or y = 6 × 9 × 10⁶
= 5.4 × 10⁶
Hence, 1.2 kg of sugar contains 5.4 × 10⁶ crystals.

Question 8.
Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road for 72 km. What would be her distance covered in the map?
Answer:
Let the distance on map is x cm.

∵ It is a case of direct variation
\(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) ⇒ \(\frac{18}{1}=\frac{72}{x}\)
or 18 × x = 72 × 1
or x = \(\frac{1 \times 72}{18}\) = 1 × 4 = 4
Thus, the required distance on the map is 4 cm.

Question 9.
A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time (1) the length of the shadow cast by another pole 10 m 50 cm high (ii) the height of a pole which casts a shadow 5m long.
Answer:
(i) Let the required length of shadow be x cm.

The more will be the height of pole, the more would be the length of shadow formed. So, it is in direct proportion.
∴ \(\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}\) ⇒ \(\frac{560}{320} = \frac{1050}{x}\)
⇒ x × 560 = 1050 × 320
⇒ x = \(\frac{1050 \times 320}{560}\) = 600 cm = 6 m

(ii) Again, we have

∴ \(\frac{560}{320}=\frac{y}{500}\)
⇒ y × 320 = 500 × 560
⇒ y = \(\frac{500 \times 560}{320}\)
= 875 cm = 8 m 75 cm

Question 10.
A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Answer:
Let the truck travels x km in 5 hours. Then, we have,

Clearly, it is a case of direct variation.
∴ \(\frac{14}{\frac{25}{60}}=\frac{x}{5}\)
or \(\frac{14 \times 60}{25}=\frac{x}{5}\)
or x = \(\frac{14 \times 60 \times 5}{25}\)
or x = \(\frac{14 \times 60}{5}\) = 14 × 12 = 168
Hence, the truck travels 168 km in 5 hours.