RBSE Solutions for Class 8 Maths Chapter 11 Mensuration Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 11 Mensuration Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 11 Mensuration Intext Questions

(Page - 169)

Class 8 Maths Chapter 11 Try These Solutions Question 1.
This is a figure of a rectangular park, whose length is 30 m and width is 20 m.

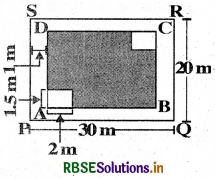
(i) What is the total length of the fence surrounding it?
(ii) How much land is occupied by the park?
(iii) There is a path of one metre width running inside along the perimeter of the park that has to be cemented. If 1 bag of cement is required to cement 4 m² area, how many bags of cement would be required to construct the cemented path?
(iv) There are two rectangular flower beds of size 1,5 m × 2 m each in the park as shown in the diagram and the rest has grass on it. Find the area covered by grass.
Answer:
(i) Total length of the fence surrounding the figure
= perimeter of park
= 2(length + breadth)
= 2 (30 + 20) m
= 2 × 50 m
= 100 m

(ii) Land occupied by the park
= Area of the park = length × breadth
= (30 × 20) m²
= 600 m²

(iii) Here, length PQ = 30 m,
breadth = QR = 20 m
.'. Area of PQRS = (30 × 20) m²
= 600 m²
length AB = (30 m - 2 m)
= 28 m²
breadth BC = (20 m - 2 m)
= 18 m
Area ABCD = (28 × 18) m²2 = 504 m²
Now area of the cemented path
= Area of PQRS - Area ABCD = (600 - 504) m² = 96 m²

The number of cement bags used
= \(\frac{\text { Area of cemented path }}{\text { Area cemented by } 1 \text { bag }}\)
= \(\frac{96}{4}\) = 24 bags.

(iv) Area of two rectangular flower beds of size 1.5 m × 2 m
= (2 × 1.5 × 2) m²
= 6 m²

Area covered by grass
= Area ABCD - Area of 2 flower beds
= (504 - 6) m² = 498 m²

Area covered by grass
= 498 m²

 

(Page 170)

Mensuration Class 8 Try These Solutions Question 1.
Match the following:

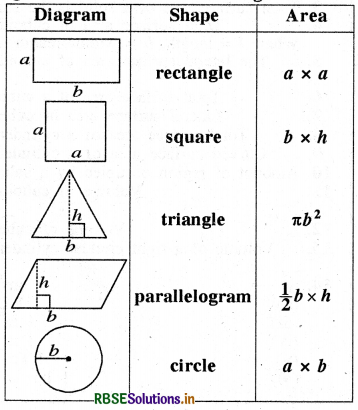
Can you write an expression for the perimeter of each of the above shapes?
Answer:

An expression for perimeter of each of the above shapes is as below :
Rectangle : 2(a + b) .
Square : 4a
Triangle : Sum of three sides
Parallelogram : 2 × sum of the adjacent sides
Circle : 2πb

(Try These - Page 170)

Class 8 Maths Mensuration Try These Solutions Question 1.
(a) Match the following figures with their respective areas in the box.

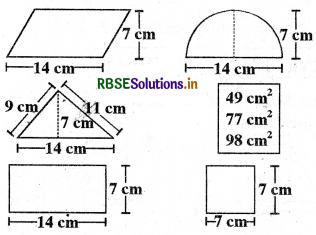
Answer:
Matching of figures with their respective areas is given below :

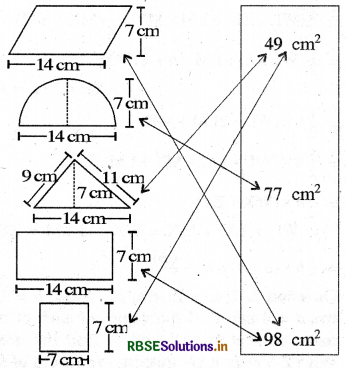
(b) Write the perimeter of each shape.
Answer:
The perimeters of respective shapes are
(i) 2(14 + a) cm, where a cm is the adjacent side.
(ii) (\(\frac{22}{7}\) × 4 + 14)cm = 36 cm
(iii) (14 +11 + 9) cm = 34 cm
(iv) 2 (14 + 7) cm = 42 cm
(v) (4 × 7) cm = 28 cm

(Try These - Page 172)

Class 8 Mensuration Try These Question 1.
Nazma’s sister also has a trapezium-shaped plot. Divide it into three parts as shown in the figure. Show that the area of trapezium WXYZ = h\(\frac{(a+b)}{2}\)

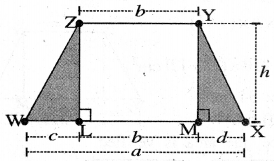
Answer:
Let L and M be the foot of perpendiculars from Z and Y on WX respectively.
Then, area of trapezium WXYZ
= Area of tight ΔWLZ + Area of rectangle LMYZ + Area of right A MXY
= \(\frac{1}{2}\)(WL × ZL) + LM × MY × \(\frac{1}{2}\)(MX × YM)
= \(\frac{1}{2}\)(WL × h) + LM × h + \(\frac{1}{2}\)(MX × h) [∵ ZL = MY = h]
= \(\frac{1}{2}\) × (WL + 2LM + MX)
= \(\frac{1}{2}\) × (WL + LM + MX + LM)
= \(\frac{1}{2}\)h × (WX + ZY) [∵ WL + LM + MX = WX and LM = ZY]
= \(\frac{1}{2}\)h × (a + b) = h\(\frac{(a+b)}{2}\)

Class 8 Maths Ch 11 Try These Question 2.
If h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm, find the values of each of its parts separately and add to find the area WXYZ.Verify it by putting the values of h, a and b in the expression h\(\frac{(a+b)}{2}\).
Answer:
Clearly, on taking h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm
Then, a = c + b + d = (6 + 12 + 4) cm = 22 cm
Area of trapezium WXYZ
= Area of ΔWLZ + Area of rect. LMYZ + Area of ΔMXY
= \(\frac{1}{2}\) × c × h + \(\frac{1}{2}\) × b × h + \(\frac{1}{2}\) × d × h
= (\(\frac{1}{2}\) × 6 × 10 + 12 × 10 + \(\frac{1}{2}\) × 4 × 10)cm²
= (30 + 120 + 20) cm² = 170 cm²

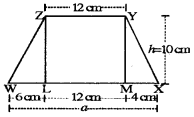
Also by formula,
Area of trap, WXYZ = \(\frac{1}{2}\) × h × (a + b)
= \(\frac{1}{2}\) × 10 × (22 + 12) cm²
= 5 x 34 cm²
= 170 cm²
Hence, the area is verified.

(Do This - Page 172)

Try These Mensuration Class 8 Question 1.
Draw any trapezium WXYZ on a piece of graph paper as shown in the figure and cut it out as shown in figure.

Answer:

Try These Solutions Class 8 Mensuration Question 2.
Find the mid-point of XY by folding the side and name it A as shown in figure.

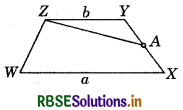
Answer:

Try These Solutions Class 8 Chapter 11 Pg 176 Question 3.
Cut trapezium WXYZ into two pieces by cutting along ZA. Place ΔZYA as shown in fig. Where AT is placed on AX.

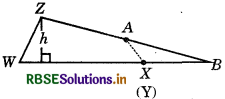
What is the length of the base of the larger triangle? Write an expression for the area of this triangle as shown in fig.
Answer:
WB = WX + XB
= WX + ZY
= a + b

Try These Solutions Class 8 Chapter 11 Question 4.
The area of this triangle and the area of the trapezium WXYZ are same (How?). Get the expression for the area of trapezium by using the expression for the area of triangle.
Answer:
Area of this triangle
= \(\frac{\text { Base } \times \text { height }}{2}=\frac{\mathrm{WB} \times h}{2}=\frac{(a+b) \times h}{2}\)
= Area of the trapezium WXYZ

(Try These - Page 173)

Try These Class 8 Mensuration Question 1.
Find the area of the following trapeziums:

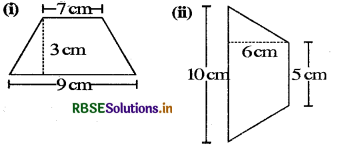
Answer:
(i) Area = \(\frac{1}{2}\)(9 + 7) × 3 cm²
= \(\frac{1}{2}\) × 16 × 3cm²
= 8 × 3 cm² = 24 cm²

(ii) Area= \(\frac{1}{2}\)(10 + 5) × 6cm²
= \(\frac{1}{2}\) × 15 × 6 cm² = 15 × 3 cm² = 45 cm²

(Do This - Page 173)

Class 8 Maths Chapter 11 Try These Question 1.
Check if the following trapeziums are of equal areas but have different perimeters.

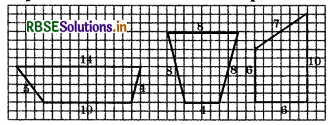
Answer:
Perimeter of the first trapezium
= 5 + 10 + 4 + 14 = 33 units
Perimeter of the second trapezium
= 8 + 4 + 8 + 8 = 28 units
Perimeter of the third trapezium
= 6 + 6+10+ 7 = 29 units
Area of the first trapezium
= \(\frac{1}{2}\) × (10 + 14) × 4 = 48 square units
Area of the second trapezium
= \(\frac{1}{2}\) × (4 + 8) × 8 = 48 square units
Area of the third trapezium
= \(\frac{1}{2}\) × (6 + 10) × 6 = 48 square units
We cannot say that figures equal in area need to be congruent. These figures are not congruent. Draw at least three trapeziums which have different areas but equal perimeters on a square sheet.

(Try These - Page 174)

Maths Formulas For Class 8 Question 1.
We know that parallelogram is also a quadrilateral. Let us also split such a P b Q quadrilateral into two triangles, find their areas and hence that of the parallelogram Does this agree with the formula that you know already?

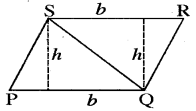
Answer:
Area of parallelogram PQRS
= Area of ΔPQS + Area of ΔQRS
= \(\frac{1}{2}\) × b × h + \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × (b + b) × h
= \(\frac{1}{2}\) × 2b × h = bh
We know the formula for the area of trapezium.

Let us use it.
Area of parallelogram ABCD
= \(\frac{1}{2}\) × ( sum of parallel sides) × distance between these sides
= \(\frac{1}{2}\) × (b + b) × h
= \(\frac{1}{2}\) × 2b × h = b × h
Yes, the result agrees with the known formula

(Think, Discuss And Write - Page 175)

Mensuration Class 8 Question 1.
A parallelogram is divided into two congruent triangles by drawing a diagonal across it. Can we divide a trapezium into two congruent triangles?
Answer:
A trapezium cannot be divided into two congruent triangles.

(Try These - Page 175)

Mensuration Formula Chart Class 8 Question 1.
Find the area of these quadrilaterals (see figure):

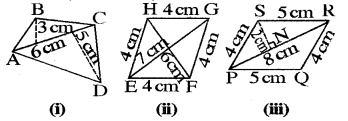
Answer:
(i) Area of the quadrilateral ABCD = Area (ΔABC) + Area (ΔACD)
= \(\frac{1}{2}\) × 6 × 3 + \(\frac{1}{2}\) × 6 × 5 cm²
= (3 × 3 + 3 × 5) cm² = (9 + 15) cm² = 24 cm²

(ii) Area of the quadrilateral EFGH
= Area of rhombus EFGH = \(\frac{1}{2}\) × EG × FH
= \(\frac{1}{2}\) × 7 × 6 cm² = 21cm²

(iii) Area of the quadrilateral PQRS
= Area of parallelogram PQRS = 2 × Area of A PSR
= 2 × \(\frac{1}{2}\) × PR × SN
= (8 × 2) cm² = 16 cm²

(Try These - Page 176)

Mensuration Chapter Question 1.
(i) Divide the following polygons into parts (triangles and trapezium) to find out its area.

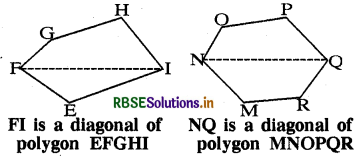
Answer:
The polygon EFGHI is divided into parts as shown.

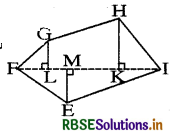
Area of polygon = Area (ΔEFI) + Area (ΔFLG) + Area (trap. LKHG) + Area (ΔHKI)
= \(\frac{1}{2}\) × FI × EM + \(\frac{1}{2}\) × FL × GL + \(\frac{1}{2}\)(KH + LG) × LK + \(\frac{1}{2}\) × KI × KH
The polygon MNOPQR is divided into parts as shown.

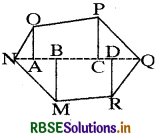
Area of polygon MNOPQR = Area (ΔMBN) + Area (trap. MBDR) + Area (ΔRDQ) + Area (ΔPCQ) + Area (trap. CPOA) + Area (ΔOAN)
= \(\frac{1}{2}\) × BN × MB + \(\frac{1}{2}\) × (DR + MB) × BD + \(\frac{1}{2}\) × QD × RD+ \(\frac{1}{2}\) × CQ × PC + \(\frac{1}{2}\) × (CP + AO) × AC + \(\frac{1}{2}\) × NA × OA

(ii) Polygon ABODE is divided into parts as shown below (Fig.)

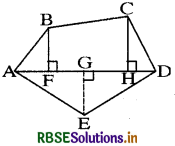
Find its area if AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and perpendiculars BF = 2 cm, CH = 3 cm, EG = 2.5 cm.
Answer:
Area of polygon ABODE = Area of ΔAFB + Area of trap. FBCH + area of ΔCHD + Area of ΔADE
= \(\frac{1}{2}\) × AF × BF + \(\frac{1}{2}\) ×(BF + CH) × FH + \(\frac{1}{2}\) × HD × CH + \(\frac{1}{2}\) × AD × GE
= \(\frac{1}{2}\) × 3 × 2cm² + \(\frac{1}{2}\) × (2 + 3) × 3cm² + \(\frac{1}{2}\) × 2 × 3cm² + \(\frac{1}{2}\) × 8 × 2.5cm²
[∵ FH = AH - AF = (6 - 3) cm = 3 cm]
and HD = AD - AH = (8 - 6) cm = 2 cm]
= (3 + \(\frac{15}{2}\) + 3 + 10)cm²
= \(\left(\frac{6+15+6+20}{2}\right)\)cm²
= \(\frac{47}{2}\)cm² = 23\(\frac{1}{2}\)cm²

(iii) Find the area of polygon MNOPQR if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm NA, OC, QD and RB are perpendiculars to diagonal MP.

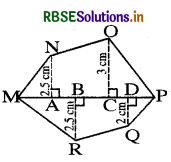
Answer:
Area of Polygon MNOPQR = Area of ΔMAN + Area of trap. ANOC + Area of ΔOOP + Area of ΔMBR + Area of trap. RBDQ + Area of ΔQDP
= \(\frac{1}{2}\) ×MA × AN + \(\frac{1}{2}\) ×(AN + CO) × AC + \(\frac{1}{2}\) × CP × CO + \(\frac{1}{2}\) × MB × RB + \(\frac{1}{2}\) ×(RB + QD) × BD + \(\frac{1}{2}\) ×DP × QD
= \(\frac{1}{2}\) × 2 × 2.5cm² + \(\frac{1}{2}\) ×(2.5 + 3) × 4cm² + \(\frac{1}{2}\) × 3 × 3 cm² + \(\frac{1}{2}\) × 4 × 2.5 cm² + \(\frac{1}{2}\) × (2.5 + 2) × 3 cm² + \(\frac{1}{2}\) × 2 × 2 cm²
[∵ AC - MC - MA = (6 - 2) = 4 cm, CP = MP - MC = (9 - 6) cm = 3 cm, BD = MD - MB = (7 - 4) = 3 cm and DP = MP - MD = (9 - 7) cm = 2 cm]
= (2.5 + 11 + 4.5 + 5 + 6.75 + 2) cm²
= 31.75 cm²

(Think Discuss And Write - Page 180)

Class 8 Chapter 11 Maths Question 1.
Why is it incorrect to call the solid shown here a cylinder?

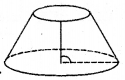
Answer:
Since the cylinder has congruent circular faces parallel to each others. So it is incorrect to call the solid shown in the figure a cylinder.

(Try These - Page 181)

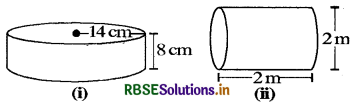
Question 1.
Find the total surface area of the following cuboids :

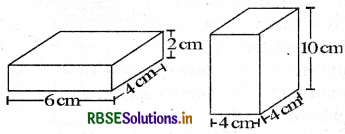
Answer:
(i) Given
Length = 6 cm, breadth = 4 cm and height = 2 cm
The total surface area of cuboid = 2 (lb + bh + hl)
= 2(6 × 4 + 4 × 2 + 2 × 6)
= 2 (24 + 8 + 12)
= 2 × 44 = 88 cm²

(ii) Given
Length = 4 cm, breadth = 4 cm and height = 10 cm
The total surface area of cuboid = 2 (lb + bh + hl)
= 2(4 × 4 + 4 × 10 + 10 × 4)
= 2 (16 + 40 + 40)
= 192 cm²

(Think, Discuss And Write - Page 181)

Question 1.
Can we say that the total surface area of cuboid = lateral surface area + 2 × area of base?
Answer:
Yes, we can say that the total surface area of the cuboid
= lateral surface + 2 × area of base

Question 2.
If we interchange the lengths of the base and the height of a cuboid [Fig (i)] to get another cuboid [Fig (ii)], will its

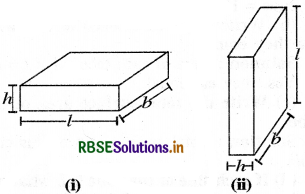
Answer:
Lateral Surface area of cuboid (i)
= 2(l + b) h
and, lateral surface area of cuboid (ii)
= 2 (h + b) × l
Clearly, these results are different. Hence, by changing the position of cuboid, its lateral surface area changes.

(Do This - Page 182)

Question 1.
Draw the pattern shown on a squared paper and cut it out [Fig. 1 (i)]. (You know that this pattern is a net of a cube. Fold it along the lines [Fig. 1 (ii)] and tape the edges to form a cube [Fig. 1 (iii)].


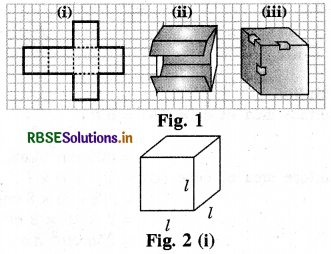
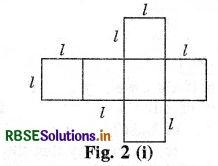
(a) What is the length, width and height of the cube? Observe that all the faces of a cube are square in shape. This makes length, height and width of a cube equal [Fig. 2 (i)].
Answer:

Length of the cube = Width of the cube = Height of the cube = l
(b) Write the area of each of the faces. Are they equal?
Answer:
Area of each face = l × l = l²
Yes, they are equal.

(c) Write the total surface area of this cube.
Answer:
Total surface area of this cube = 6 l².

(d) If each side of the cube is l, what will be the area of each face? [Fig 2 (ii)]
Can we say that the total surface area of a cube of side l is 6PI
Answer:
Area of each face of the cube = l × l = l²
Yes, we can say that the total surface area of a cube of side l is 6l².

(Try These - Page 182)

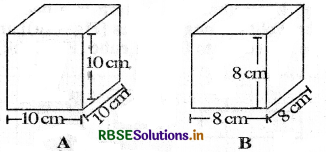
Question 1.
Find the surface area of cube A and lateral surface area of cube B.

Answer:
Surface area of cube (A) = 6l²
= 6(10)² cm²
= 600 cm²

Surface area of cube (B) = 2(l + l) × l
= 2(8 + 8) × 8 cm²
= 2 × 16 × 8 cm²
= 256 cm²

(Think, Discuss And Write - Page 183)

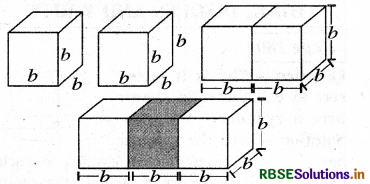
Question 1.
(i) Two cubes each with side ft are joined to form a cuboid. What is the surface area of this cuboid? Is it 12b²? Is the surface area of cuboid formed by joining three such cubes, 18b²? Why?

(ii) How will you arrange 12 cubes of equal length to form a cuboid of smallest surface area?
(iii) After the surface area of a cube is painted, the cube is cut into 64 smaller cubes of same dimensions.
How many have no face painted? 1 face painted? 2 faces painted? 3 faces painted?

Answer:
(i) If two cubes are joined end to end, we get a cuboid such that
L = Length = b + b = 2b units
B = Breadth = b units
H = Height = b units

Surface area of the cuboid = 2 (LB + BH + LH)
= 2(2b × b + b × b + 2b × b) sq. units
= 2(2b² + b² + 2b²) sq. units.
= 10b² sq. units.
So, it is not 12b²
If three cubes are joined end to end, then the dimensions of the cuboid so formed are as below :
L = Length = 3b, B = Breadth = b, and H = Height = b
∴ The surface area of cuboid = 2(LB + BH + LH)
= 2(3b × b + b × b + 3b × b) sq. units
= 2(3b² + b² + 3b²) sq. units
= 14b² sq. units So, it is not 18b².

(ii) 12 cubes of equal length can be arranged to form a cuboid as below:
(a)

In this case : l = 12b, b = b and h = b
∴ Its surface area = 2(12b × b + b × b + 12b × b)
= 2(12b² + b² + 12b²)
= 50 b²

(b)

In this case: l = 6b, b = b and h = 2b
∴ Its surface area = 2(6b × b + b × 2b + 6b × 2b)
= 2(6b² + 2b² + 12b²) = 40b²

(c)

In this case: l = 4b, b = b and h = 3b
∴ Its surface area = 2(4b × b + b × 3b + 4b × 3b)
= 2(4b² + 3b² + 12b²)
= 38b²
Hence, to have the smallest surface area, cubes may be arranged as shown in (c).

(iii) Number of cubes having no face painted = 16
Number of cubes having one face painted = 16

(Try These - Page 184)

Question 1.
Find the total surface area of the following cylinders:

Answer:
(i) Here, r = 14 cm and h = 8 cm
Total surface area = 2πrh + 2πr²
= (2 × \(\frac{22}{7}\) × 14 × 8 + 2 × \(\frac{22}{7}\) × 14 × 140cm²
= (704 + 1232) cm² = 1936 cm²

(ii) Here, r = \(\frac{2}{2}\)m = 1 m and h = 2 m
Total surface area = 2πrh + 2πr²
= (2 × \(\frac{22}{7}\) × 1 × 2 + 2 × \(\frac{22}{7}\) × 1 × 1)m²
= (\(\frac{88}{7}+\frac{44}{7}\)) m² = \(\frac{132}{7}\)m²
= 18\(\frac{6}{7}\)m²

(Think, Discuss And Write - Page 184)

Question 1.
Note that lateral surface area of a cylinder is the circumference of base x height of cylinder. Can we write lateral surface area of a cuboid as perimeter of base x height of cuboid?
Answer:

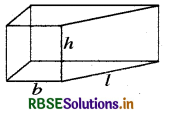
We know that Lateral surface area of the cuboid = 2 (l + b) × h
= Perimeter of the base × height
Thus, we can write the lateral surface area of a cuboid as perimeter of base × height of cuboid.

(Try These - Page 187)

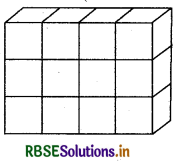
Question 1.
Take 36 cubes of equal size (i.e., length of each cube is same). Arrange them to form a cuboid. You can arrange them in many ways. Observe the following table

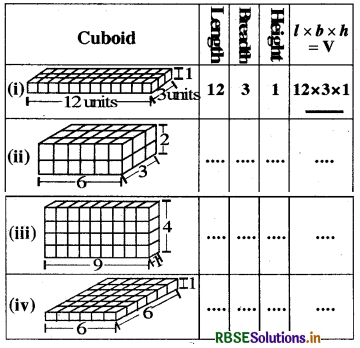
What do you observe?
Answer:
On filling the blank, the table is given below :

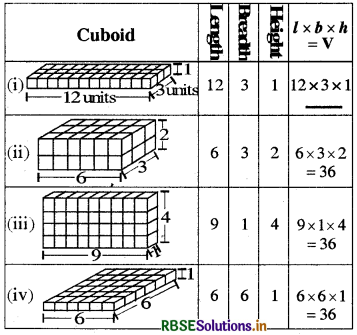
We observe that we have used 36 cubes to form these cuboids. So their volumes in each case is 36 cubic units. Clearly, it is equal to length × breadth × height.

(Try These - Page 188)

Question 1.
Find the volume of the following cuboids.

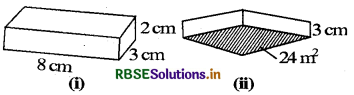
Answer:
(i) Volume of the cuboid
= (8 × 3 × 2) cm³ = 48 cm³
(ii) Volume of the cuboid
_ = Area of the base × height
= (24 × \(\frac{3}{100}\))m³ = 0.72 m³

(Page 189)

Question 1.
Find the volume of the following cubes
(a) with a side 4 cm
(b) with a side 1.5 m.
Answer:
(a) Volume of the cube
= (Side)³
= (4)³ cm³
= 64 cm³
(b) Volume of the cube = (Side)³
= (1.5)³ m³ = 3.375 m³

(Do This - Page 189)

Question 1.
Arrange 64 cubes of equal size in as many ways as you can to form a cuboid. Find the surface area of each arrangement. Can solid shapes of same volume have same surface area?
Answer:
Some arrangements are as follows :

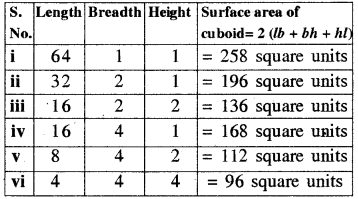
Also, volume of the cuboid obtained in each case is 64 cubic units.
So, now we cannot say that solid shapes of same volume need to have same surface area.

(Think, Discuss And Write - Page 189)

Question 1.
A company sells biscuits. For packing purpose they are using cuboidal boxes : box A → 3 cm × 8 cm × 20 cm, box B → 4 cm × 12 cm × 10 cm. What size of the box will be economical for the company? Why? Can you suggest any other size (dimensions) which has the same volume but is more economical than these?
Answer:
Box A :
Volume = (3 × 8 × 20) cm³ = 480 cm³
Surface Area = 2(3 × 8 + 8 × 20 + 20 × 3) cm²
= 2(24 + 160 + 60) cm²
= 2 × 244 cm²
= 488 cm²

Box B : Volume = (4 × 12 × 10) cm³ = 480 cm²
Surface Area = 2(4 × 12 + 12 × 10 + 10 × 4)cm²
= 2(48 + 120 + 40) cm²
= 2 × 208 cm²
= 416 cm²

Clearly Volume of a box of type B
= Volume of a box of type A.
But, the surface area of a box of type B is less than that of a box of type A.
Thus, material required for box B is less.
Box B is more economical than box A.

Box of size 8 cm × 6 cm × 10 cm, i.e., of volume 400 cm³
Its surface area = 2(48 + 60 + 80) cm²
= 2 (188) cm² = 376 cm²
Clearly, its surface area is less than that of box B. So, it is more economical than the given boxes.

(Try These - Page 189)

Question 1.
Find the volume of the following cylinders.

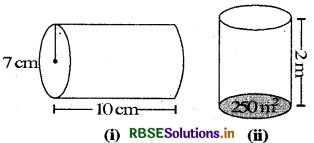
Answer:
(i) Volume of cylinder = πr²h Where, r = 7 cm, h = 10 cm
= (\(\frac{22}{7}\) × 7 × 7 × 10)cm³
_ = 1540 cm³

(ii) Volume of cylinder
= (Area of the base) × height
= (250 × 2) m³ = 500 m³