RBSE Solutions for Class 8 Maths Chapter 11 क्षेत्रमिति Ex 11.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 11 क्षेत्रमिति Ex 11.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.2

Class 8 Maths Chapter 11 Exercise 11.2 In Hindi प्रश्न 1.
एक मेज के ऊपरी पृष्ठ ( सतह) का आकार समलम्ब जैसा है। यदि इसकी समान्तर भुजाएँ 1m और1.2 m हैं तथा इन समान्तर भुजाओं के बीच की दूरी 0.8 m है, तो इसका क्षेत्रफल ज्ञात कीजिए।

हल:
मेज के ऊपरी पृष्ठ का क्षेत्रफल
= समलम्ब का क्षेत्रफल = \(\frac{1}{2}\) × (समान्तर भुजाओं का योग) × (उनके बीच की दूरी)
= [\(\frac{1}{2}\) × (1 + 1.2) × 08]m²
= (\(\frac{1}{2}\) × 2.2 × 0.8)m²
= (1.1 × 0.8) m²
= 0.88 m² 

11.2 Class 8 Hindi Medium प्रश्न 2.
एक समलम्ब का क्षेत्रफल 34 cm है और इसकी ऊँचाई 4 cm है। समान्तर भुजाओं में से एक की 10 cm लम्बाई है। दूसरी समान्तर भुजा की लम्बाई ज्ञात कीजिए।
हल:
माना कि वांछित भुजा की लम्बाई x cm है।
तब, समलम्ब का क्षेत्रफल = [\(\frac{1}{2}\) × (10 + x) × 4 ]cm²
= 2(10 + x) cm²
परन्तु, समलम्ब का क्षेत्रफल = 34 cm² (दिया है)
∴ 2(10 + x) = 34
या 10 + x = 17
या x = 17 - 10 = 7
अतः, दूसरी समान्तर भुजा की लम्बाई = 7 cm 

Class 8 Maths Chapter 11.2 Hindi Medium प्रश्न 3.
एक समलम्ब के आकार के खेत ABCD की बाड़ की लम्बाई 120 m है। यदि BC = 48 m, CD = 17 m और AD = 40 m है, तो A इस खेत का क्षेत्रफल ज्ञात कीजिए। भुजा AB समान्तर भुजाओं AD तथा BC पर लम्ब है।

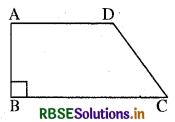
हल:
माना कि दिया गया समलम्ब ABCD है जिसमें BC = 48 m, CD = 17 m और AD = 40 m D से, DL ⊥ BC खींचिए। 

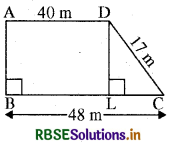
अब, BL = AD = 40 m और LC = BC - BL
= (48 - 40) m.
= 8m 

समकोण ΔDLC में पाइथागोरस प्रमेय लगाने पर 
DL² = DC² - LC²
= 17² - 8² = 289 - 64 = 225 
या DL = \(\sqrt{225}\) = 15 m

अब, समलम्ब ABCD का क्षेत्रफल
= \(\frac{1}{2}\) × (BC+ AD) x DL 
= \(\frac{1}{2}\) × (48 + 40) × 15m²
= (44 × 15) m² = 660 m² 

Class 8 Maths Chapter 11 Exercise 11.2 Solutions In Hindi प्रश्न 4.
एक चतुर्भुज आकार के खेत का विकर्ण 24 m है और शेष सम्मुख शीर्षों से इस विकर्ण पर खींचे गए लम्ब 8 m एवं 13 m हैं। खेत का क्षेत्रफल ज्ञात कीजिए।

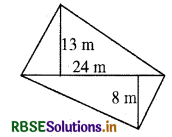
हल:
माना कि दिया गया D. चतुर्भुज ABCD है जिसमें BE ⊥ AC और DF ⊥ AC हैं। दिया है कि

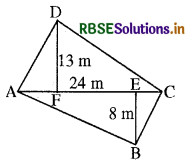
AC = 24 m, BE = 8 m
तथा DF = 13 m

अब, चतुर्भुज ABCD का क्षेत्रफल = ΔABC का क्षेत्रफल + ΔACD का क्षेत्रफल 
= \(\frac{1}{2}\) × AC × BE + \(\frac{1}{2}\) × AC × DF
= [(\(\frac{1}{2}\) × 24 × 8)+ (\(\frac{1}{2}\) × 24 × 13)]m²
= (12 × 8 + 12 × 13) m²
= (96 + 156) m²
= 252 m²

11.2 Class 8 In Hindi प्रश्न 5.
किसी समचतुर्भुज के विकर्ण 7.5 cm एवं 12 cm हैं। इसका क्षेत्रफल ज्ञात कीजिए। 
हल:
समचतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) × (विकर्णों का गुणनफल)
= (\(\frac{1}{2}\) × 7.5 × 12)cm²
= 45 cm² 

कक्षा 8 प्रश्नावली 11 पॉइंट 2 प्रश्न 6.
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए | जिसकी भुजा 6 cm और शीर्षलम्ब 4 cm है। यदि एक विकर्ण की लम्बाई 8 cm है तो दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हल:
माना कि ABCD एक समचतुर्भुज है जिसकी एक भुजा 6 cm है तथा जिसका शीर्ष लम्ब DE = 4 cm है। आगे, इसका एक विकर्ण BD = 8 cm है। समचतुर्भुज ABCD का क्षेत्रफल

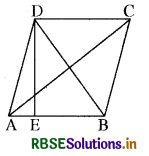
= 2 × क्षेत्रफल (ΔABD) 
= 2 × \(\frac{1}{2}\) × AB × DE 
= (6 × 4) cm²
= 24 cm²

आगे, समचतुर्भुज ABCD का क्षेत्रफल
= \(\frac{1}{2}\) × AC × BD
या \(\frac{1}{2}\) × AC × 8 = 24
या AC = 6 cm 
अतः, दूसरे विकर्ण की लम्बाई 6 cm है।

Class 8 Maths 11.2 Solutions In Hindi प्रश्न 7.
किसी भवन के फर्श में समचतुर्भुज के आकार की 3000 टाइलें हैं और इनमें से प्रत्येक के विकर्ण 45 cm एवं 30 cm लम्बाई के हैं। 4 रुपए प्रति वर्ग मीटर की दर से इस फर्श को पॉलिश करने का व्यय ज्ञात कीजिए।
हल:
फर्श का क्षेत्रफल= 3000 × एक टाइल का क्षेत्रफल
= 3000 × \(\frac{1}{2}\) × 45 × 30cm 
= 1500 × 45 × 30 cm 
= \(\frac{1500 \times 45 \times 30}{100 \times 100}\) m²
= 202.5 m²

4 रुपए प्रति वर्ग मीटर की दर से फर्श को पॉलिश करने का व्यय
= (4 × 202.5) रुपए 
= 810 रुपा

Class 8 Maths 11.2 In Hindi प्रश्न 8.
मोहन एक सडक समलम्ब के आकार का खेत खरीदना चाहता है। इस खेत की नदी के साथ वाली भुजा सड़क के साथ वाली भुजा के समान्तर है और लम्बाई में दुगुनी है। यदि इस खेत का क्षेत्रफल 10,500 m है और दो समान्तर भुजाओं के बीच की लम्बवत् दूरी 100 m है, तो नदी के साथ वाली भुजा की लम्बाई ज्ञात कीजिए। 

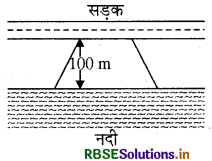
हल:
माना कि समलम्ब के आकार के खेत की समान्तर भुजाएँ x m तथा 2x m हैं । तब, इसका क्षेत्रफल
= \(\frac{1}{2}\)(x + 2x) × 100m
= 50 × 3x m²
= 150x m²
परन्तु दिया है कि खेत का क्षेत्रफल 10500 m² है।
150x = 10500 
या x= 10500 = 70 
∴ नदी के साथ वाली भुजा की लम्बाई 2 × 70 अर्थात्, 140 मीटर है। 

प्रश्नावली 11.2 प्रश्न 9.
एक ऊपर उठे हुए चबूतरे का ऊपरी पृष्ठ अष्टभुज के आकार का है, जैसा कि आकृति में दर्शाया गया है। अष्टभुजी पृष्ठ का क्षेत्रफल ज्ञात कीजिए।

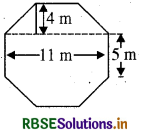
हल:

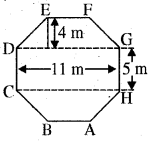
अष्टभुजी पृष्ठ ABCDEFGH का क्षेत्रफल = क्षेत्रफल (समलम्ब ABCH) + क्षेत्रफल (आयत HCDG) + क्षेत्रफल (समलम्ब GDEF) 
= [\(\frac{1}{2}\)(5 + 11) × 4 + 11 × 5 + \(\frac{1}{2}\) (11 + 5) × 4]m²
= (32 + 55 + 32) m² = 119 m²

11.2 Class 8 प्रश्न 10.
एक पंचभुज आकार का बगीचा है जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो विभिन्न तरीकों से विभाजित किया। दोनों तरीकों का उपयोग करते हुए इस बगीचे का क्षेत्रफल ज्ञात कीजिए। क्या आप इसका क्षेत्रफल ज्ञात करने की कोई और विधि बता सकते हैं?

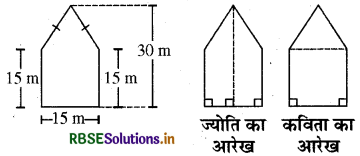
हल:
ज्योति का तरीका

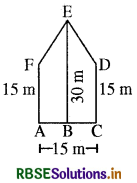
पंचभुजाकार बगीचे का क्षेत्रफल = 2 × समलम्ब ABEF का क्षेत्रफल
= 2 × \(\frac{1}{2}\) × (15 + 30) × \(\frac{15}{2}\)m²
= (45 × \(\frac{15}{2}\))m = 337.5m²

कविता का तरीका

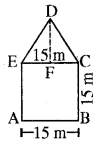
पंचभुजाकार बगीचे का क्षेत्रफल
= क्षेत्रफल (वर्ग ABCE) + क्षेत्रफल (ΔDEC)
= [15 × 15 + \(\frac{1}{2}\) × 15 × 15]m²
= (225 + 112.5) m² 
= 337.5 m² 

हाँ, इसका क्षेत्रफल ज्ञात करने का

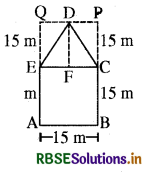
अन्य तरीका निम्न है
वांछित क्षेत्रफल ABCDEA
= क्षेत्रफल (आयत ΔBPQ) - 2 × क्षेत्रफल (ΔCPD) 
= (15 × 30)m - 2 × \(\frac{1}{2} \times \frac{15}{2}\) × 15m²
= (450 - \(\frac{225}{2}\))m² = \(\left(\frac{900-225}{2}\right)\)m²
= \(\frac{675}{2}\) m² 
= 337.5m²

Class 8 Maths 11.2 प्रश्न 11. 
संलग्न पिक्चर फ्रेम के आरेख की बाहरी एवं अंतः विमाएँ क्रमशः 24 cm  28 cm एवं 16 cm  20 cm हैं। यदि फ्रेम के प्रत्येक खण्ड की चौड़ाई समान है, तो प्रत्येक खण्ड का क्षेत्रफल ज्ञात कीजिए।

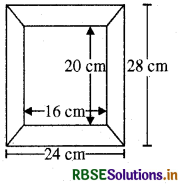
हल:
स्पष्ट रूप से, फ्रेम की चौड़ाई
= \(\frac{\mathrm{AB}-\mathrm{PQ}}{2}=\frac{24-16}{2}\)cm 
= \(\frac{8}{2}\)cm = 4cm
अब, खंड ABQP का क्षेत्रफल
= खंड DCRS का क्षेत्रफल 
= \(\frac{1}{2}\) × (AB+ PQ) × 4cm 
= 2(24 + 16) cm²
= 2 × 40 cm = 80 cm² 

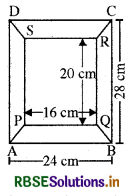
और खंड APSD का क्षेत्रफल 
= खंड CBQR का क्षेत्रफल 
= \(\frac{1}{2}\) × (AD+ PS) × 4cm²
= 2(28 + 20)cm²
= 2 × 48 cm²
= 96 cm²