RBSE Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 11 Mensuration Ex 11.2

Question 1.
The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.

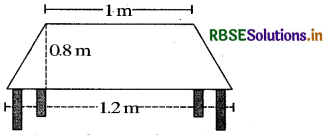
Answer:
Area of top surface of a table
= Area of the trapezium
= \(\frac{1}{2}\) × (sum of parallel sides) × (distance between them)
= \(\frac{1}{2}\) × (1 + 1.2) × 0.8]m²
= (\(\frac{1}{2}\) × 2.2 × 0.8)m²
= (1.1 × 0.8) m²
= 0.88 m²

Question 2.
The area of a trapezium is 34 cm² and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.
Answer:
Let the required other side = x cm
Then, area of the trapezium
= [\(\frac{1}{2}\) × (10 + x) × 4]cm²
= 2(10 + x) cm²
But, the area of the trapezium = 34 cm² (given)
∴ 2(10 + x) = 34
or 10 + x = 17
or x = 17 - 10 = 7
Hence, the other side = 7 cm

Question 3.
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

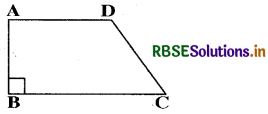
Answer:
Let ABCD be the given trapezium in which BC = 48 m, CD = 17 m and AD = 40 m

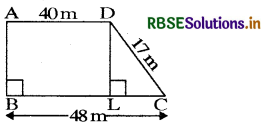
Now, BL = AD = 40 m and LC = BC - BL
= (48 - 40) m = 8m
Applying Pythagoras theorem in ∆ DLC, we have
DL² = DC² - LC²
= 17² - 8² = 289 - 64 = 225
or DL = √225 = 15 m
Now, area of trapezium ABCD
= \(\frac{1}{2}\) × (BC + AD) × DL
= \(\frac{1}{2}\) × (48 + 40) × 15m²
= (44 × 15) m²
= 660 m²

Question 4.
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. the field.

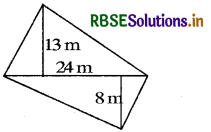
Answer:
Let ABCD be the given quadrilateral in which BE ⊥ AC and DF ⊥ AC.
It is given that
AC = 24 m, BE = 8 m and DF = 13 m
Now, Area of quadrilateral ABCD
= Area of ∆ ABC + Area of ∆ ACD
= \(\frac{1}{2}\) × AC × BE + \(\frac{1}{2}\) × AC × DF
= [(\(\frac{1}{2}\) × 24 × 8) + (\(\frac{1}{2}\) × 24 × 3)]m²
= (12 × 8 + 12 × 13) m²
= (96 + 156) m²
= 252 m²

Question 5.
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Answer:
Area of rhombus = \(\frac{1}{2}\) × (product of diagonals)
= (\(\frac{1}{2}\) × 7.5 × 12)cm²
= 45 cm²

Question 6.
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Answer:
One side of rhombus = 5 cm
Height = 4.8 cm
Diagonal d₁ = 8 cm
Let the length of other diagonal d₂ of rhombus = x cm
∵ Rhombus is a special type of parallelogram.
∴ Area of rhombus = Base × height
= 5 × 4.8 cm² = 24 cm²
Also, Area of rhombus
= \(\frac{1}{2}\) × (product of diagonals)
⇒ 24 = \(\frac{1}{2}\) × 8 × x
⇒ 24 = 4x
⇒ x = 6 cm
So, the other diagonal is 6 cm long.

Question 7.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is ₹ 4.
Answer:
Area of the floor = 3000 × Area of one tile
= 3000 × \(\frac{1}{2}\) × 45 × 30cm²
= 1500 × 45 × 30 cm²
= \(\frac{1500 \times 45 \times 30}{100 \times 100}\) m²
= 202.5 m²
Cost of polishing the floor @ ₹ 4 per m²
= ₹ (4 × 202.5)
= ₹ 810

Question 8.
Road Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the River side along the road. If the area of this field is 10,500 m² and the perpendicular distance

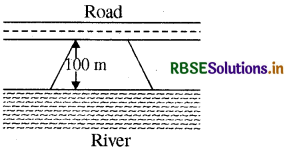
between the two parallel sides is 100 m, find the length of the side along the river.
Answer:
Let the one side of the river = x m = b₁
∴ Other side (parallel to the road)
= \(\frac{1}{2}\) × m = b₂
h = 100 m
∴ Area of trapezium = \(\frac{1}{2}\) × (b₁ + b₂) × h
or 10,500 m² = \(\frac{1}{2}\) × (x + 2x) × 100
or 10,500 m² = \(\frac{1}{2}\) × 3x × 100
or 10,500 m2² = 150 x
or \(\frac{10,500}{150}\) = x
or 70 = x ⇒ x = 70 m
∴ one side = 70 m,
other side = 2 × 70 = 140 m

Question 9.
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

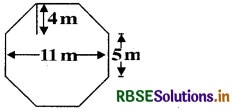
Answer:

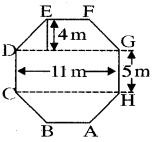
Area of the octagonal surface ABCDEFGH
= Area (trapezium ABCH) + Area (rectangle HCDG) + Area (trapezium GDEF)
= [\(\frac{1}{2}\)(5 + 11) × 4 + 11 × 5 + \(\frac{1}{2}\)(11 + 5) × 4]m²
= (32 + 55 + 32) m²
= 119 m²

Question 10.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.

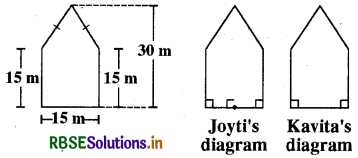
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Answer:
Jyoti’s diagram:

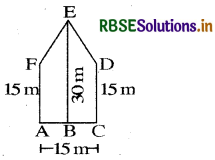
Area of the pentagonal shaped park .
= 2 × Area of trapezium ABEF
= 2 × \(\frac{1}{2} \)× (15 + 30) × \(\frac{15}{2}\)m²
= (45 × \(\frac{15}{2}\))m² = 337.5 m²

Kavita’s diagram:

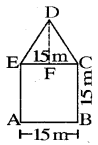
Area of the pentagonal shaped park
= Area (rectangle ABCE) + Area (∆ DEF)
= [15 × 15 + \(\frac{1}{2}\) × 15 × 15]m²
= (225 + 112.5) m²
= 337.5 m²
Yes, the other method of finding its area is given below :
Required area ABCDEA
= Area (rectangle ABPQ) - 2 × Area (∆ CPD)

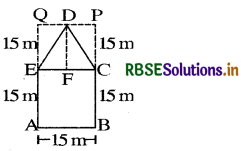
= (15 × 30)m² - 2 × \(\frac{1}{2}\) × \(\frac{15}{2}\) × 15m²
= (450 - \(\frac{225}{2}\))m² = \(\left(\frac{900-225}{2}\right)\)m²
= \(\frac{675}{2}\)m² = 337.5m²

Question 11.
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.

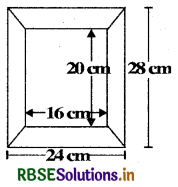
Answer:
Clearly, the width of the frame
= \(\frac{\mathrm{AB}-\mathrm{PQ}}{2}\) = \(\frac{24-16}{2}\)cm
= \(\frac{8}{2}\)cm = 4 cm

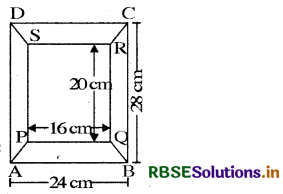
Now, Area of section ABQP = Area of section DCRS
= \(\frac{1}{2}\) × (AB + PQ) × 4cm²
= 2(24 + 16) cm²
= 2 × 40 cm² = 80 cm²
and, area of section APSD = area of section CBQR
= \(\frac{1}{2}\) × (AD + PS) × 4cm²
= 2(28 + 20)cm²
= 2 × 48 cm² = 96 cm²