RBSE Solutions for Class 8 Maths Chapter 11 क्षेत्रमिति Ex 11.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 11 क्षेत्रमिति Ex 11.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 11 क्षेत्रमिति Ex 11.1

प्रश्न 1. 
जैसा कि नीचे दी गई आकृति में दर्शाया गया है, एक आयताकार और एक वर्गाकार खेत के माप दिए हुए हैं। यदि इनके परिमाप समान हैं, तो किस खेत का क्षेत्रफल अधिक होगा?

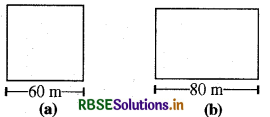
हल:
माना कि आयत की चौडाई है। यह दिया है कि आयत का परिमाप = वर्ग का परिमाप।
∴ 2(80+ x) = 4 × 60
या 80 + x = \(\frac{4 \times 60}{2}\) = 120
या x = 120 - 80
= 40

अर्थात् आयत की चौड़ाई = 40 m
अब, वर्ग का क्षेत्रफल = (60 × 60) m²
= 3600 m²
और आयत का क्षेत्रफल = (40× 80) m²
= 3200 m²

अतः, वर्गाकार खेत का क्षेत्रफल अधिक है।

प्रश्न 2.
श्रीमती कौशिक के पास चित्र में दर्शाए गए मापों वाला एक वर्गाकार प्लाट है। वह प्लॉट के बीच जज में एक घर बनाना चाहती हैं। घर के चारों ओर एक बगीचा विकसित किया गया है। 55 रुपए प्रति वर्ग के मीटर की दर से इस बगीचे को विकसित करने का व्यय ज्ञात कीजिए।

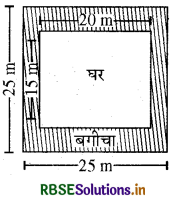
हल:
बगीचे का क्षेत्रफल = बाहरी वर्ग का क्षेत्रफल - आंतरिक आयत का क्षेत्रफल
= 25 × 25 m- - 20 × 15 m²
= (625 - 300) m² = 325 m²
55 रुपए प्रति वर्ग मीटर की दर से बगीचे को विकसित करने में लगी रकम = (55 × 325) रुपए
= 17875 रुपए 

प्रश्न 3.
जैसा कि आरेख में दर्शाया गया है, एक बगीचे का आकार मध्य में आयताकार है और किनारों पर अर्धवृत्त के रूप में है। इस बगीचे का परिमाप और क्षेत्रफल ज्ञात कीजिए [आयत की लम्बाई 20 - (3.5 + 3.5) मीटर है।

हल:
बगीचे का कुल क्षेत्रफल = आयताकार भाग का क्षेत्रफल + दो अर्द्धवृत्ताकार भागों के क्षेत्रफल का योग
= (13 × 7)m² + (2 × \(\frac{1}{2} \times \frac{22}{7}\) × 3.5 × 3.5)m²
= (91 + 38.5)m²
= 129.5 m²
बगीचे का परिमाप = 2 × आयताकार भाग की लम्बाई + वृत्त की परिधि = (2 × 13 + 2 × \(\frac{22}{7}\) × 3.5)m 
= (26 + 22) m = 48 m

प्रश्न 4.
फर्श बनाने के लिए उपयोग की जाने वाली एक टाइल का आकार समान्तर चतुर्भुज का है जिसका आधार 24 cm और संगत ऊँचाई 10 cm है। 1080 वर्ग मीटर क्षेत्रफल के एक फर्श को ढकने के लिए ऐसी कितनी टाइलों की आवश्यकता है? (फर्श के कोनों को भरने के लिए आवश्यकतानुसार आप टाइलों को किसी भी रूप में तोड़ सकते हैं।)
हल:
एक टाइल का क्षेत्रफल = आधार × ऊँचाई
= (24 × 10) cm²  = 240 cm

फर्श को ढकने के लिए आवश्यक टाइलों की संख्या

प्रश्न 5.
एक चींटी किसी फर्श पर बिखरे हुए विभिन्न आकारों के भोज्य पदार्थ के टुकड़ों के चारों ओर घूम रही है। भोज्य पदार्थ के किस टुकड़े के लिए चींटी को लम्बा चक्कर लगाना पड़ेगा? स्मरण रखिए, वृत्त की परिधि सूत्र c = 2πr, जहाँ । वृत्त की त्रिज्या है, की सहायता से प्राप्त की जा सकती है।

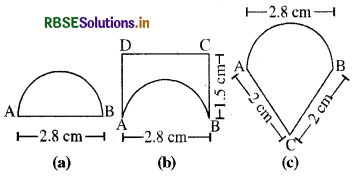
हल:
दी गई आकृति में जैसा कि दिखाया गया है, बिन्दु A, B, C तथा D चिह्नित कीजिए। माना कि चींटी प्रत्येक आकार के भोज्य पदार्थ के टुकड़े के चारों ओर घूमना बिन्दु A से प्रारम्भ करती है। उसे प्रत्येक टुकड़े का पूरा चक्कर लगाकर पुनः बिन्दु A पर आना है। 
(a) भोज्य पदार्थ का टुकड़ा (a) के लिए
तय की गई दूरी = चाप AB + BA
= \(\frac{1}{2}\) × 2πr +2.8cm
जहाँ, r = 1.4 cm है
= \(\frac{22}{7}\) × 1.4cm + 2.8cm
= 4.4 cm + 2.8 cm = 7.2 cm

(b) भोज्य पदार्थ का टुकड़ा (b) के लिए-
तय की गई दूरी = चाप AB + BC + CD + DA
= \(\frac{1}{2}\) × 2πr +1.5 cm + 2.8cm + 1.5 cm
जहाँ, r = 1.4 cm है
= \(\frac{22}{7}\) × 1.4cm + 5.8cm
=4.4 cm + 5.8 cm = 10.2 cm 

(c) भोज्य पदार्थ का टुकड़ा (c) के लिए
तय की गई दूरी = चाप AB + BC + CA 
= \(\frac{1}{2}\) × 2πr +2 cm + 2 cm
जहाँ, r = 1.4 cm है 
= \(\frac{22}{7}\) × 1.4cm + 4cm
= 4.4 cm + 4 cm = 8.4 cm
स्पष्टतः चींटी को भोज्य पदार्थ के टुकड़े (b) के लिए अधिक दूरी तय करनी पड़ेगी।