RBSE Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 11 Mensuration Ex 11.1

Question 1.
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?

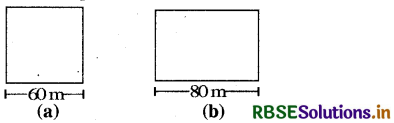
Answer:
Let x be the breadth of the rectangle. It is given that the perimeter of rectangle = perimeter of square
∴ 2(80 + x) = 4 × 60
or 80 + x = 120
or x = 120 - 80 = 40
i.e.,breadth of the rectangle = 40 m
Now, area of the square = (60 × 60) m²
= 3600 m²
and, the area of the rectangle = (40 × 80) m²
= 3200 m²
Since 3600 m² > 3200 m²
∴ Area of the square field (a) is greater.

Question 2. 
Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m².

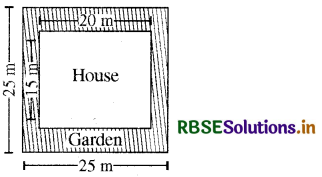
Answer:
Area of garden = Area of the outer square - Area of the inner rectangle
= 25 × 25 m² - 20 × 15 m²
= (625 - 300) m² = 325 m²
Cost of developing a garden @ ₹ 55 per sq. meter
= ₹ (55 × 325)
= ₹ 17,875

Question 3.
The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 - (3.5 + 3.5) metres].

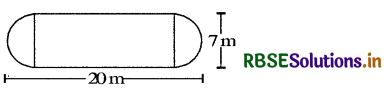
Answer:
Total area of the garden
= Area of the rectangular portion + The sum of the areas of the pair of semicircle
= (13 × 7)m² + (2 × \(\frac{1}{2}\) × \(\frac{22}{7}\) × 3.5 × 3.5)m²
= (91 + 38.5)m²
= 129.5 m²
Perimeter of the garden = 2 × length of the rectangular portion + circumference of circle
= (2 × 13 + 2 × \(\frac{22}{7}\) × 3.5)m
= (26 + 22) m = 48 m

Question 4.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the comers).
Answer:
Area of parallelogram = Base × corresponding height
Area of each tile = \(\left(\frac{24}{100} \times \frac{10}{100}\right)\)m²
= \(\frac{24}{10000}\) m² = 0.024 m²
∴ Area of the floor = 1080 m²
Now, number of tiles = \(\frac{\text { Total Area }}{\text { Area of each tile }}\)
= \(\frac{1080}{0.024}\)
= 45,000 tiles

Question 5.
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food- piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.

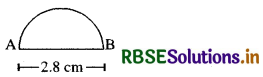
Answer:
(a) Diameter = 2.8 cm 2 8
⇒ Radius = \(\frac{2.8}{2}\) cm = 1.4 cm
Perimeter of a circle = 2πr
Perimeter of a semi-circle = \(\frac{2 \pi r}{2}\) = πr
∴ Perimeter of the figure = πr + Diameter
= \(\frac{22}{7}\) × 1.4 cm + 2.8 cm
= \(\left(\frac{22}{7} \times \frac{14}{10}+2.8\right)\) cm
= 7.2 cm

(b) Perimeter of the semi-circle part
= πr = \(\frac{22}{7}\) × 1.4 cm
= 4.4 cm
Perimeter of the remaining part
= 1.5 cm + 2.8 cm + 1.5 cm
= 5.8 cm
∴ Perimeter of the figure
= 4.4 cm + 5.8 cm
= 10.2 cm

(c) Perimeter of the semi-circular part
= \(\frac{\pi d}{2}=\frac{22}{7} \times \frac{2.8}{2}\) = 4.4 cm
∴ Perimeter of the figure
= 4.4 cm + 2 cm + 2 cm
= 8.4 cm
Since, 7.2 cm < 8.4 cm < 10.2 cm
Clearly, the ant have to take a longer round in case of food piece (b).