RBSE Solutions for Class 8 Maths Chapter 10 Visualizing Solid Shapes Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 10 Visualizing Solid Shapes Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 10 Visualizing Solid Shapes Intext Questions

(Do This page No: 153)

Question 1.
Match the following: (First one is done for you)

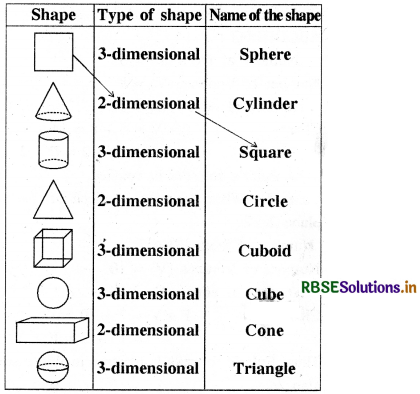
Answer:
Matching is shown as below-

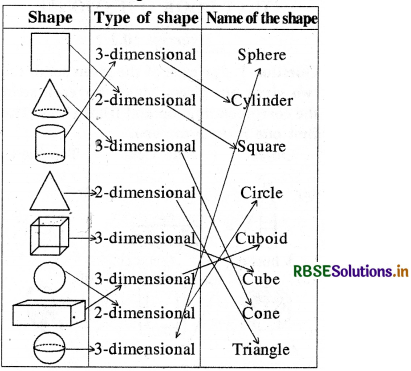
(Do This page No: 154)

Question 1.
Match the following pictures (objects) with their shapes:

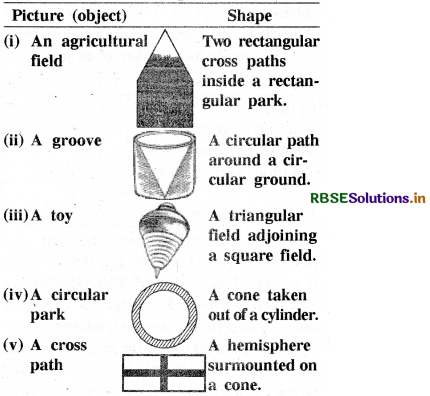
Answer:

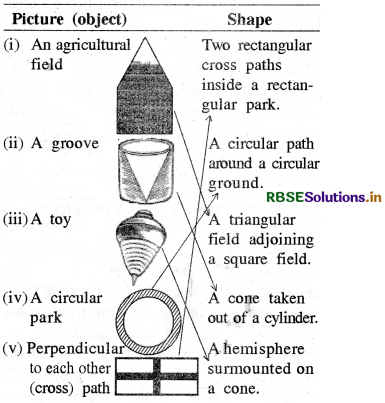
(Do This Page No: 165)

Question 1.
Tabulate the number of faces, edges and vertices for the following polyhedrons : (Here ‘V’ stands for number of vertices, ‘F’ stands for number of faces and ‘E’ stands for number of edges).

What do you infer from the last two columns? In each case, do you find F + V = E + 2, he., F + V - E = 2? This relationship is called Euler’s formula. In fact this formula is true for any polyhedron.
Answer:
On tabulating the number of faces (F), edges (E) and vertices (V) for the following polyhedrons, we have

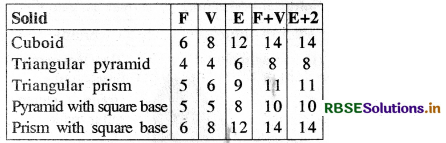
From the last two columns, we find that
F + V = E + 2, i.e.'F + V - E = 2
This relation is called Euler’s formula.

(Think, Discuss And Write Page No: 166)

Question 1.
What happens to F, V and E if some parts are sliced off from a solid? (To start with, you may take a plasticine cube, cut a corner off and investigate).
Answer:
Let ABCDHEFG be a plasticine cube. This cube is sliced off by a plane XYZ, where X, Y and Z are the points of file coterminus edges FG, FE and FB respectively.
From the adjoining figure:

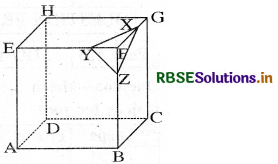
Case I : In cube ABCDHEFG:
Number of faces (F) - 6
Number of Vertices (V) = 8
Number of edges (E) = 12
Clearly, F + V = 6 + 8 = 14 .
= 12 + 2 = E + 2
Thus Euler’s formula is verified.

Case II: When the cube is sliced off by a plane XYZ.
Number of faces (F) = 7
Number of Vertices (V) = 10
Number of edges (E) = 15
Clearly, F + V = 7 + 10 = 17
= 15 + 2 = E + 2
Thus, Euler’s formula holds true in this case also.