RBSE Solutions for Class 8 Maths Chapter 10 ठोस आकारों का चित्रण Ex 10.3

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 10 ठोस आकारों का चित्रण Ex 10.3 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 10 ठोस आकारों का चित्रण Ex 10.3

प्रश्न 1.
क्या किसी बहुफलक के फलक नीचे दिए अनुसार हो सकते हैं?
(i) 3 त्रिभुज
(ii) 4 त्रिभुज
(iii) एक वर्ग और चार त्रिभुज।
हल:
हम जानते हैं कि बहुफलक एक ठोस होता है जो चार या अधिक बहुभुज फलकों से इस प्रकार घिरा होता है कि इसकी दो फलकें एक किनारे पर मिलती हैं तथा तीन या अधिक किनारे एक शीर्ष बिन्दु पर मिलते हैं। इसलिए,
(i) एक बहुफलक के फलक तीन त्रिभुज नहीं हो सकते हैं।
(ii) एक बहुफलक के फलक चार त्रिभुज हो सकते हैं।
(iii) एक बहुफलक के फलक एक वर्ग और चार त्रिभुज हो सकते हैं।

प्रश्न 2.
क्या ऐसा बहुफलक सम्भव है जिसके फलकों की संख्या कोई भी संख्या हो?
हल:
हाँ, यह तभी सम्भव है जब फलकों की संख्या चार से अधिक या बराबर है।

प्रश्न 3.
निम्नलिखित में से कौन-कौन प्रिज्म हैं?

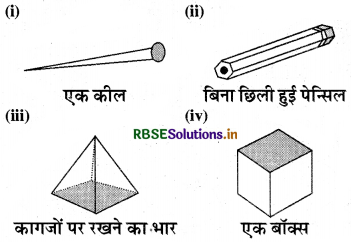
हल:
हम जानते हैं कि प्रिज्म एक बहुफलक है जिसकी दो फलकें समान्तर तल में सर्वांगसम बहुभुज हैं तथा जिसकी अन्य फलकें समान्तर चतुर्भुज हैं।
अतः

• एक कील प्रिज्म नहीं है।
• एक बिना छिली पेन्सिल एक प्रिज्म है।
• कागजों पर रखने का भार प्रिज्म नहीं है।
• एक बॉक्स प्रिज्म है।

प्रश्न 4.
(i) प्रिज्म और बेलन किस प्रकार एक जैसे हैं?
(ii) पिरामिड और शंकु किस प्रकार एक जैसे हैं?
उत्तर:
(i) एक प्रिज्म एक बेलन तब हो जाता है जब उसके आधार की भुजाओं की संख्या अधिक-से-अधिक होती जाती है।
(ii) एक पिरामिड एक शंकु तब हो जाता है जब उसके आधार की भुजाओं की संख्या अधिक से अधिक होती जाती है।

प्रश्न 5.
क्या एक वर्ग प्रिज्म और एक घन एक ही होते हैं? स्पष्ट कीजिए।
उत्तर:
नहीं। एक वर्ग प्रिज्म और एक घन एक नहीं होते हैं। यह घनाभ भी हो सकता है।

प्रश्न 6.
इन ठोसों के लिए ऑयलर सूत्र का सत्यापन कीजिए।

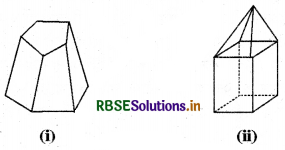
हल:
(i) इस आकृति में,
F = 7, V = 10, E = 15
 F + V = 7 + 10 = 17 और E + 2 = 15 + 2 = 17
या F + V = E + 2
अतः, ऑयलर सूत्र सत्यापित हुआ।

(ii) द्वितीय आकृति में,
F = 9, V = 9, E = 16
F + V = 9 +9 = 18 और E + 2 = 16 + 2 = 18
या F + V = E + 2
अतः, ऑयलर सूत्र सत्यापित हुआ।

प्रश्न 7.
ऑयलर सूत्र का प्रयोग करते हुए, अज्ञात संख्या को ज्ञात कीजिए

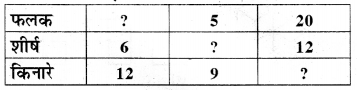
हल:
I. फलकों की संख्या = ?,
शीर्षों की संख्या = 6,
किनारों की संख्या = 12
ऑयलर सूत्र से हम जानते हैं कि
F + V = E+2
या F= E + 2 - V = 12 + 2 - 6 = 8 
अतः, फलकों की संख्या = 8 

II. फलकों की संख्या = 5,
शीर्षों की संख्या = ?,
किनारों की संख्या = 9
ऑयलर सूत्र से हम जानते हैं कि
F + V = E + 2 
या V = E + 2 - F
V = 9 + 2 - 5 = 6
अतः, शीर्षों की संख्या =6

III. फलकों की संख्या = 20,
शीर्षों की संख्या = 12,
किनारों की संख्या = ?
ऑयलर सूत्र से हम जानते हैं कि
F + V = E + 2 या E = F + V - 2
E = 20 + 12 - 2 = 30
अतः, किनारों की संख्या = 30

प्रश्न 8.
क्या किसी बहुफलक के 10 फलक, 20 किनारे और 15 शीर्ष हो सकते हैं?
हल:
क्योंकि F + V ≠ E + 2 (10 + 15 + 20 + 2)
∴ एक बहुफलक के 10 फलकें, 20 किनारे तथा 15 शीर्ष नहीं हो सकते हैं।