RBSE Solutions for Class 8 Maths Chapter 1 परिमेय संख्याएँ Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 1 परिमेय संख्याएँ Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 1 परिमेय संख्याएँ Intext Questions

(पाठगत प्रश्न - पृष्ठ 2)

प्रश्न 1.
प्राकृत संख्याओं के लिए सभी चार संक्रियाओं के अन्तर्गत संवृत गुण की जाँच कीजिए।
उत्तर:
(1) योग संक्रिया: प्राकृत संख्याएँ योग संक्रिया के अन्तर्गत संवृत हैं अर्थात् a और b दो प्राकृत संख्याएँ हैं, तो a + b भी प्राकृत संख्या होगी।
उदाहरण द्वारा जाँच-

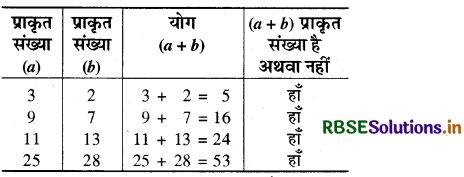
(2) व्यवकलन संक्रिया: प्राकृत संख्याएँ व्यवकलन संक्रिया के अन्तर्गत संवृत नहीं हैं। यदि a और b दो प्राकृत संख्याएँ हैं, तो a > b होने पर a - b एक प्राकृत संख्या होगी किन्तु a < b अथवा a = b होने पर प्राप्त संख्या प्राकृत संख्या नहीं होगी।
उदाहरण द्वारा जाँच-

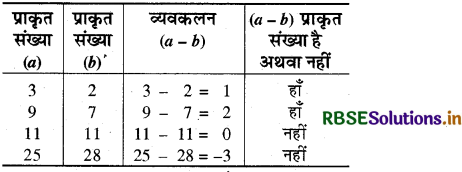
(3) गुणन संक्रिया-प्राकृत संख्याएँ गुणन संक्रिया के अन्तर्गत संवृत हैं अर्थात् a और b दो प्राकृत संख्याएँ हैं, तो उनका गुणनफल भी प्राकृत संख्या होगी।
उदाहरण द्वारा जाँच-

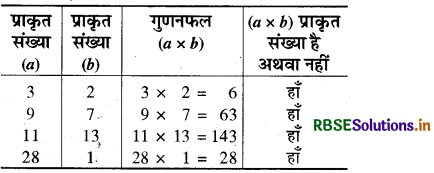
(4) भाग संक्रिया-प्राकृत संख्याएँ भाग संक्रिया के अन्तर्गत संवृत नहीं हैं।
उदाहरण द्वारा जाँच-

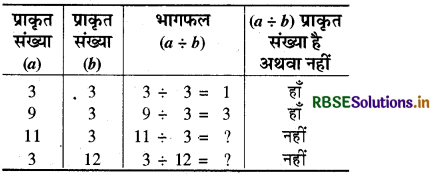
(प्रयास कीजिए - पृष्ठ 5)

प्रश्न-निम्नलिखित सारणी में रिक्त स्थानों की पूर्ति कीजिए-

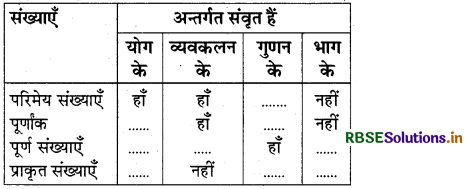
हल:

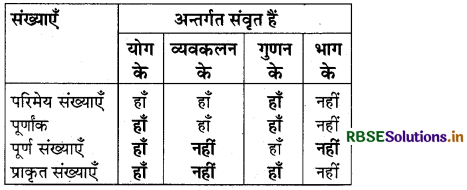
(क्रिम विनिमेयता)

प्रश्न 1.
निम्नलिखित सारणी के रिक्त स्थानों को भरते हुए विभिन्न संक्रियाओं के अन्तर्गत पूर्ण संख्याओं की क्रम विनिमेयता का स्मरण कीजिए-

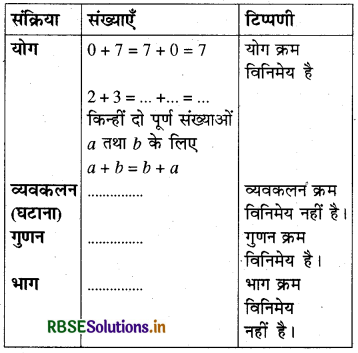
जाँच कीजिए कि क्या प्राकृत संख्याओं के लिए भी ये संक्रियाएँ क्रम विनिमेय हैं।
हल:

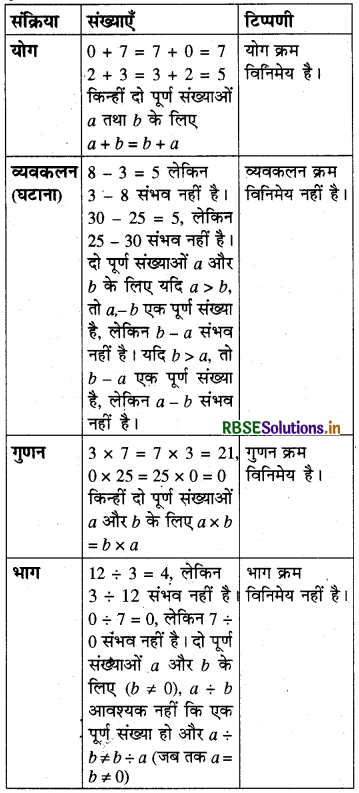
प्राकृत संख्याओं के लिए क्रम विनिमेयता की जाँच-
(1) योग में-यदि a और b कोई दो प्राकृत संख्याएँ हैं, तो (a + b) = (b + a) (योग में क्रम विनिमेयता है।)
जाँच-इस गुण की जाँच के लिए कुछ प्राकृत संख्याओं के युग्म लेकर उन्हें भिन्न-भिन्न क्रम में जोड़ने पर-

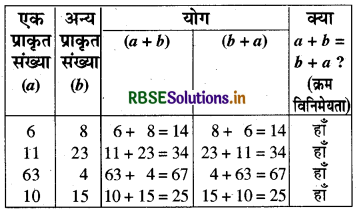
(2) व्यवकलन में-प्राकृत संख्याओं के व्यवकलन में क्रम विनिमेयता नहीं होती है अर्थात् यदि a और b दो प्राकृत संख्याएँ हैं, तो सामान्यतः (a - b) ≠ (b - a)।1
हम जानते हैं कि 8 - 3 = 5, लेकिन 3 – 8 संभव नहीं है। इसी प्रकार 100 - 25 = 75, लेकिन 25 - 100 संभव नहीं है।

(3) गुणन में-यदि a और b कोई दो प्राकृत संख्याएँ हैं, . तो (a × b) = (b × a) (गुणन में क्रम विनिमेयता है।)
जाँच-इस गुणन की जाँच के लिए प्राकृत संख्याओं के कुछ युग्म लेकर उन्हें भिन्न-भिन्न क्रम में नियमानुसार गुणन करेंगे-

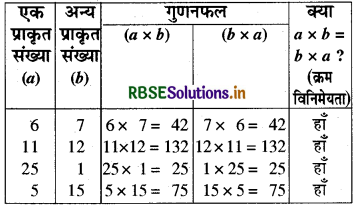
हम देखते हैं कि दो प्राकृत संख्याओं को किसी भी क्रम में गुणा करने पर गुणनफल सदैव समान ही आता है।

(4) भाग में-यदि a और b दो प्राकृत संख्याएँ हैं, तो a ÷ b ≠ b ÷ a (भाग में क्रम विनिमेयता नहीं है।)
जाँच-इस गुण की जाँच हम कुछ.युग्म लेकर निम्नानुसार करेंगे|

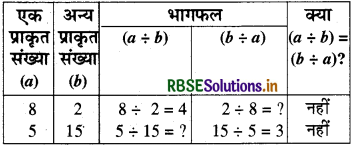
प्रश्न 2.
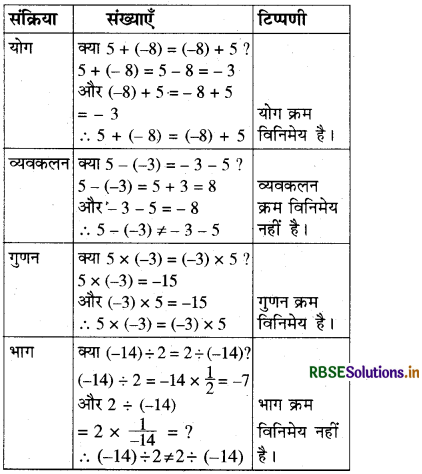
अग्रलिखित सारणी के रिक्त स्थानों को भरिए और पूर्णांकों के लिए विभिन्न संक्रियाओं की क्रम विनिमेयता जाँचिए-

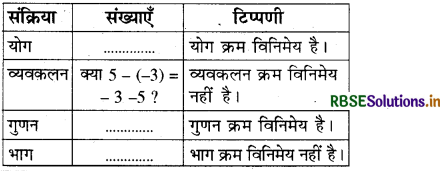
हल:

(प्रयास कीजिए - पृष्ठ 7)

प्रश्न-निम्नलिखित सारिणी को पूरा कीजिए-

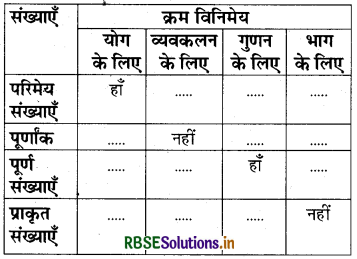
हल:

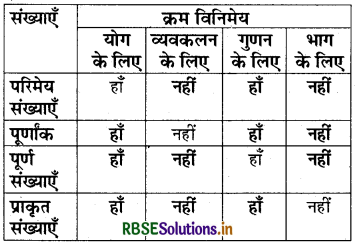
(साहचर्यता (सहचारिता)

प्रश्न 1.
निम्नलिखित सारिणी के माध्यम से पर्ण संख्याओं के लिए चार संक्रियाओं की साहचर्यता को स्मरण कीजिए-

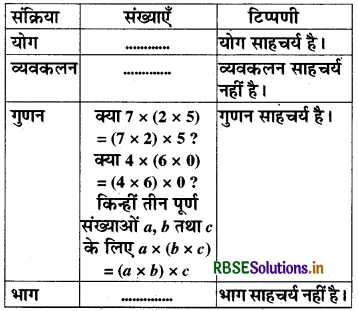
इस सारिणी को भरिए और अन्तिम स्तम्भ में दी गई टिप्पणियों को सत्यापित कीजिए। प्राकृत संख्याओं के लिए विभिन्न संक्रियाओं की साहचर्यता की स्वयं जाँच कीजिए।
हल:

प्राकृत संख्याओं के लिए विभिन्न संक्रियाओं की साहचर्यता की जाँच
(1) योग-किन्हीं तीन प्राकृत संख्याओं a, b और c के लिए (a + b) + c = a + (b + c)
जाँच-

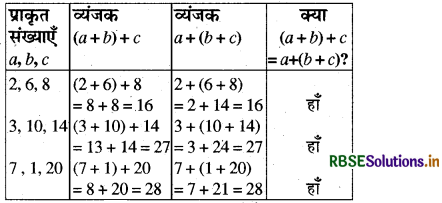
अतः प्राकृत संख्याओं का योग साहचर्य है।

(2) व्यवकलन-किन्हीं तीन प्राकृत संख्याओं a, b और c.. के लिए सामान्यतः a - (b - c) ≠ (a - b) - c
जाँच-

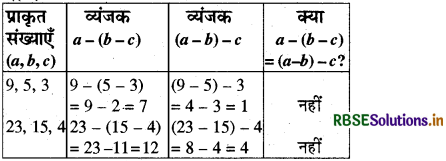
अतः प्राकृत संख्याओं का व्यवकलन साहचर्य नहीं है।

(3) गुणन-किन्हीं तीन प्राकृत संख्याओं a, b और c के लिए a × (b × c) = (a × b) × c
जाँच-

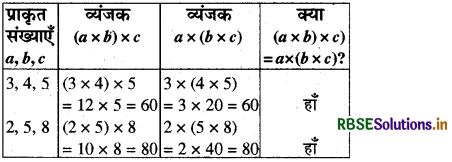
अतः प्राकृत संख्याओं का गुणन साहचर्य है।

(4) भाग-किन्हीं तीन प्राकृत संख्याओं के लिए सामान्यतः
a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c
जाँच-

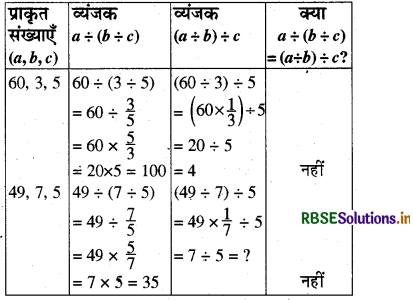
अतः प्राकृत संख्याओं का भाग साहचर्य नहीं है।

प्रश्न 2.
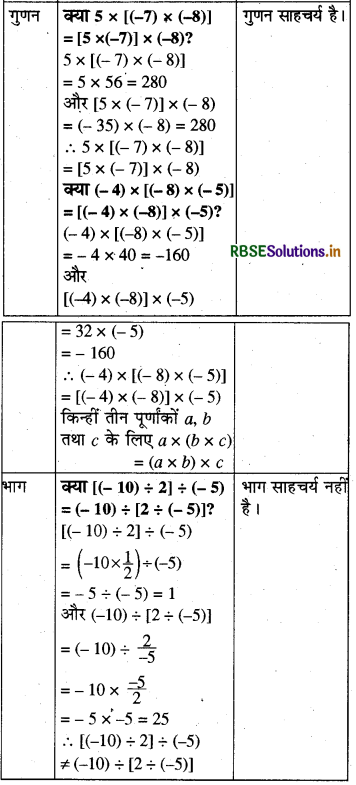
पूर्णांकों के लिए चार संक्रियाओं की साहचर्यता निम्नलिखित सारणी से जाँचिए-

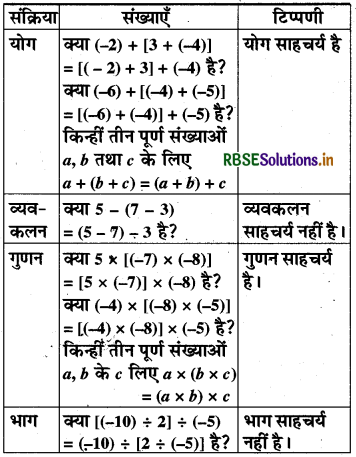
हल:

(प्रयास कीजिए - पृष्ठ 10)

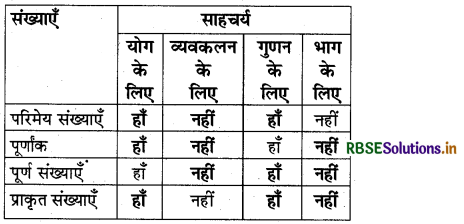
प्रश्न-निम्नलिखित सारणी को पूरा कीजिए-

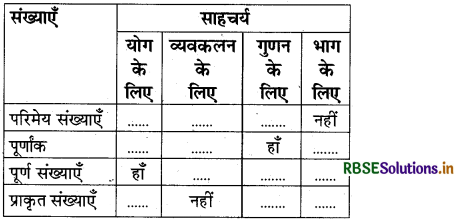
हल:

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 12)

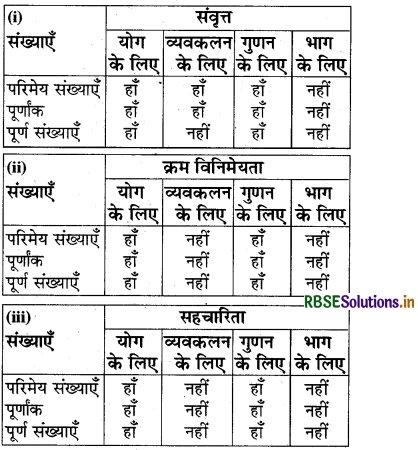
प्रश्न-यदि कोई गुणधर्म परिमेय संख्याओं के लिए सत्य है तो क्या वह गुणधर्म, पूर्णांकों, पूर्ण संख्याओं के लिए भी सत्य होगा? कौन-से गुणधर्म इनके लिए सत्य होंगे और कौन-से सत्य नहीं होंगे?
हल:
(1) निम्न गुण को छोड़कर परिमेय संख्याओं की क्रियाओं के गुण पूर्णांकों में भी होंगे a ÷ b एक परिमेय संख्या है यदि b ≠ 0 लेकिन a ÷ b जरूरी नहीं कि एक पूर्णांक हो यदि a, b ∈ I
(2) निम्न गुण को छोड़कर परिमेय संख्याओं के सभी गुण पूर्ण संख्याओं में भी होंगे
(i) यदि a और b परिमेय संख्याएँ हैं तो a - b भी परिमेय संख्या होगी। लेकिन यदि a और b पूर्ण संख्याएँ हैं तो (a - b) पूर्ण संख्या हो भी सकती है और नहीं भी।
(ii) यदि a और b परिमेय संख्याएँ हैं तो a ÷ b (b ≠ 0) एक परिमेय संख्या होगी। लेकिन a और b पूर्ण संख्याएँ हों तो a: b (b ≠ 0) जरूरी नहीं कि एक पूर्ण संख्या हो।

निम्नलिखित तालिका दर्शाती है कि परिमेय संख्याओं. पूर्णांकों तथा पूर्ण संख्याओं में कौन-सा गुण उभयनिष्ठ है/नहीं है-

(प्रयास कीजिए - पृष्ठ 14)

प्रश्न- वितरकता के उपयोग से निम्नलिखित का मान ज्ञात कीजिए-
(i) \(\left\{\frac{7}{5} \times\left(\frac{-3}{12}\right)\right\}+\left\{\frac{7}{5} \times \frac{5}{12}\right\}\)
हल:

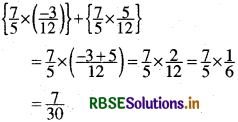
(ii) \(\left\{\frac{9}{16} \times \frac{4}{12}\right\}+\left\{\frac{9}{16} \times \frac{-3}{9}\right\}\)
हल:

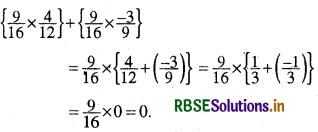
(प्रयास कीजिए - पृष्ठ 18)

प्रश्न-अक्षर द्वारा अंकित प्रत्येक बिन्दु के लिए परिमेय संख्या लिखिए-
(i)

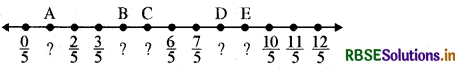
हल:
(i) अक्षर द्वारा अंकित बिन्दुओं के सम्मुख परिमेय संख्याएँ निम्नलिखित हैं-
A : \(\frac{1}{5}\)
B : \(\frac{4}{5}\)
C : \(\frac{5}{5}\)
D : \(\frac{8}{5}\)
E : \(\frac{9}{5}\)

(ii)

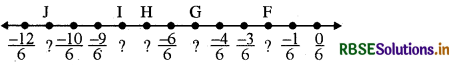
हल:
(ii) अक्षर द्वारा अंकित बिन्दुओं के सम्मुख परिमेय संख्याएँ निम्नलिखित हैं-
J : \(\frac{-11}{6}\)
I : \(\frac{-8}{6}\)
H : \(\frac{-7}{6}\)
G : \(\frac{-5}{6}\)
F : \(\frac{-2}{6} \)