RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Intext Questions

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 1 Rational Numbers Intext Questions

Question 1.
Check for closure property under all the four operations for natural numbers.
Answer:
(1) Addition: Natural numbers are closed under addition, i.e. If a and b are two natural numbers then a + b is also a natural number.
Verification by Example:

(2) Subtraction: Natural numbers are not closed under subtraction. If a and b are two natural numbers and a > b then a - b is a natural number. But if a < b or a = b, then (a - b) is not a natural number.
Verification by Example:

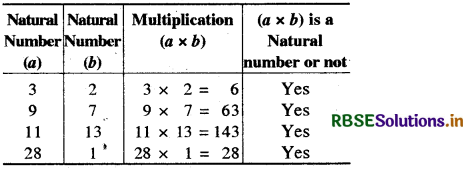
(3) Multiplication: Natural numbers are closed under multiplication. If a and b are two natural numbers, then their product is also a natural number.
Verification by Example:

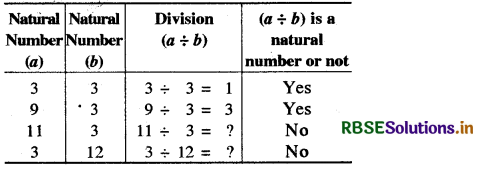
(4) Division: Natural numbers are not closed under division.
Verification by Example:

(Try These Page No: 4)

Question 1.
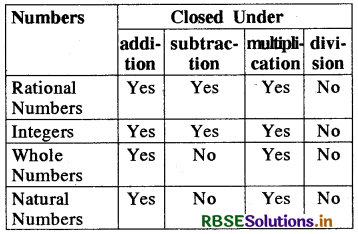
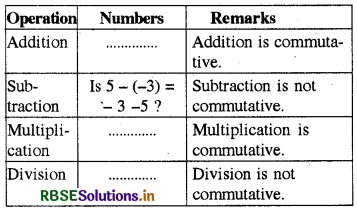
Fill in the blanks in the following table:

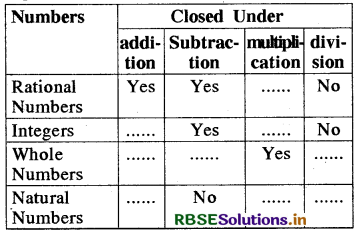
Answer:

Commutativity:

Question 1.
Recall the commutativity of different operations for whole numbers by filling the following table

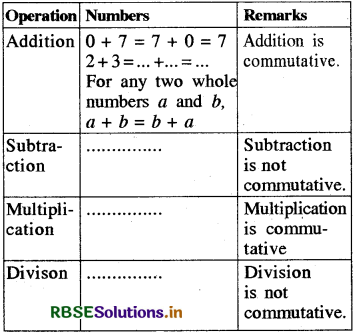
Check whether the commutativity of the operations hold for whole numbers also.
Answer:

Verification of commutativity for Natural numbers:
(1) Under Addition: If a and b are two natural numbers, then (a + b) = (b + a) (Addition is commutative)

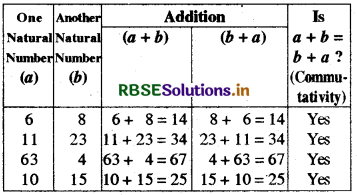
(2) Under Subtraction: The subtraction of natural numbers is not commutative, i.e., if a and b are two natural numbers, then in general (a - b) is not equal to (b - a).
We know that 8-3 = 5, but 3 - 8 is not a natural number.

(3) Under Multiplication: If a and b are any two natural numbers, then a × b = b × a (Multiplication is commutative)
Verification: In order to verify this property, let us take a few pairs of natural numbers and multiply these numbers in different orders as shown below:

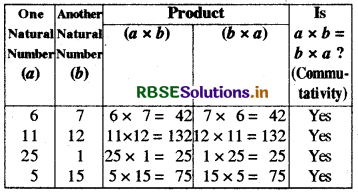
We find that in any order we multiply two natural numbers, the product remains the same.

(4) Under Division: If a and b are two natural numbers, then a ÷ b ≠ b ÷ a (Division is not commutative)
Verification: In order to verify this property let us take a few pairs of natural numbers:

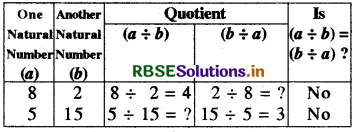
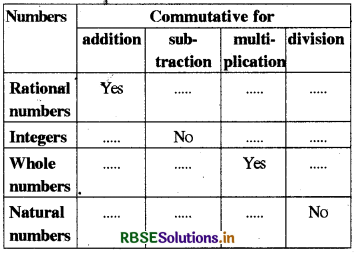
Question 2.
Fill in the following table and check the commutativity of different operations for integers:

Answer:

(Try These Page No: 6)

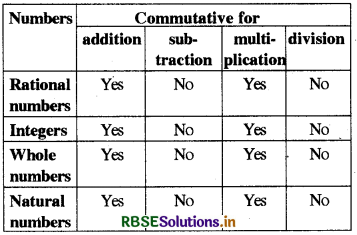
Question 1.
Complete the following table:

Answer:

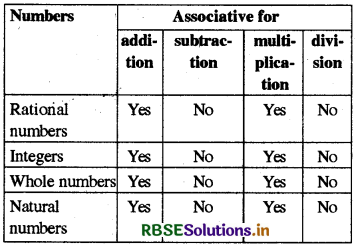
Associativity

Question 1.
Recall the associativity of the four operations for whole numbers through this table:

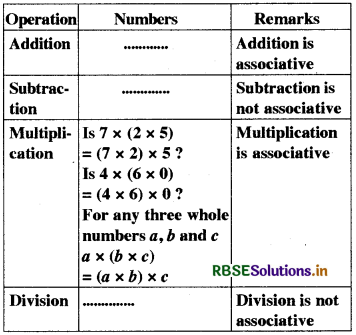
Fill in this table and verify the remarks given in the last column.
Check for yourself the associativity of different operations for natural numbers.
Answer:

Associativity for Natural Numbers:
(1) Addition: For any three natural numbers a, b and c, (a + b) + c = a + (b + c)
Verification:

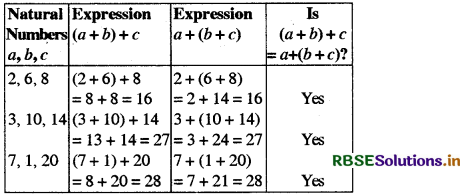
Thus, the addition of natural numbers is associative.

(2) Subtraction: For any three natural numbers a, b, and c, in general a - (b - c) = (a - b) - c
Verification:

Thus, the multiplication of natural numbers is associative.

(3) Multiplication: For any three natural numbers a, b, and c, in general a × (b × c) = (a × b) × c
Verification:

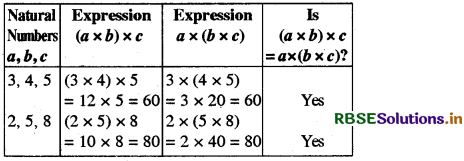
Thus, the multiplication of natural numbers is associative.

(4) Division: For any three natural numebrs, in general a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c
Verification:

Thus, the division of natural numbers is not associative.

Question 1.
Verify Associativity for the four operations for integers.

Answer:

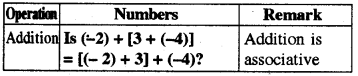
(Try These Page No: 9)

Complete the following table:

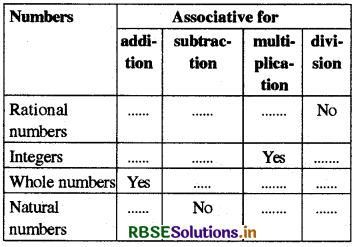
Answer:

(Think, Discuss and Write Page No: 11)

Question 1.
If a property holds for rational numbers, will it also hold for integers? For whole numbers? Which will? Which will not?
Answer:
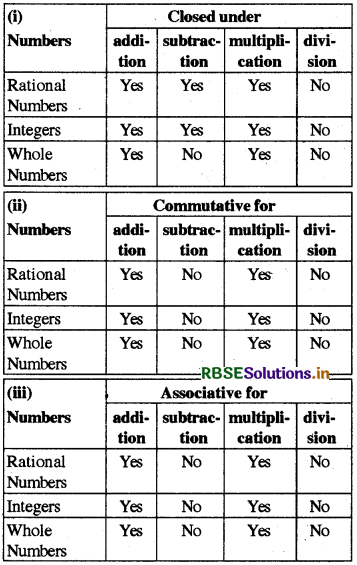
(1) Any property which is true for rational numbers is also true for integers except for any integers ‘a’ and ‘b’ (a ÷ b) is not necessarily an integer. If a, b ∈ I

(2) Similarly, all properties which are true for rational numbers, are also true for whole numbers except for any whole numbers ‘a’ and ‘b', (a ÷ b) may or may not be a whole number.
Table showing the properties of rational numbers, integers and whole numbers, which are/are not in common of rational numbers.

(Try These Page No: 13)

Question 1.
Find using distributivity
(i) \(\left\{\frac{7}{5} \times\left(\frac{-3}{12}\right)\right\}+\left\{\frac{7}{5} \times \frac{5}{12}\right\}\)
Answer:

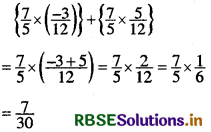
(ii) \(\left\{\frac{9}{16} \times \frac{4}{12}\right\}+\left\{\frac{9}{16} \times \frac{-3}{9}\right\}\)
Answer:

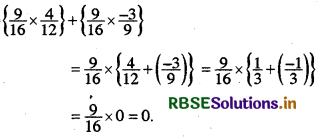
(Try These Page No: 17)

Question 1.
Write the rational number for each point labelled with a letter.
(i)

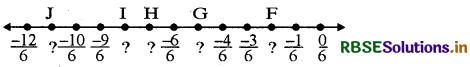
Answer:
Correct fraction to be marked against
A : \(\frac{1}{5}\)
B: \(\frac{4}{5}\)
C: \(\frac{5}{5}\)
D: \(\frac{8}{5}\)
E: \(\frac{9}{5}\)

(ii)

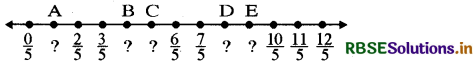
Answer:
Correct fraction to be marked against
J: \(\frac{-11}{6}\)
I: \(\frac{-8}{6}\)
H: \(\frac{-7}{6}\)
G: \(\frac{-5}{6}\)
F: \(\frac{-2}{6}\)