RBSE Solutions for Class 8 Maths Chapter 1 परिमेय संख्याएँ Ex 1.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 1 परिमेय संख्याएँ Ex 1.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 1 परिमेय संख्याएँ Ex 1.2

प्रश्न 1.
निम्नलिखित संख्याओं को संख्या रेखा पर निरूपित कीजिए
(i) \(\frac{7}{4}\)
हल:
\(\frac{7}{4}\) के लिए हम संख्या रेखा पर 0 के दायीं ओर 7 चिह्न लगाएँगे जिनमें प्रत्येक के बीच की दूरी \(\frac{1}{4}\) होगी। 0 से प्रारम्भ करेंगे और 7वाँ चिह्न \(\frac{7}{4}\) होगा।

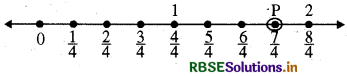
बिन्दु P, \(\frac{7}{4}\) को दर्शाता है।

(ii) \(\frac{-5}{6}\)
हल:
\(\frac{-5}{6}\) के लिए संख्या रेखा पर 0 से बायीं ओर 1 दूरी के 5 चिह्न लगाएँगे। 0 से आरम्भ करेंगे और पाँचवाँ चिह्न \(\frac{-5}{6}\) होगा। P बिन्दु परिमेय संख्या \(\frac{-5}{6}\) को दर्शाता है।

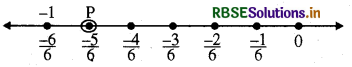
प्रश्न 2.
\(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) को संख्या रेखा पर निरूपित कीजिए।
हल:
\(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) को संख्या रेखा पर दर्शाने के लिए | शून्य पर 0 दर्शाएँगे। अब P बिन्दु संख्या रेखा पर -1 दर्शाता है।

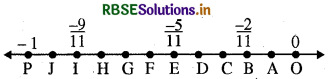
OP खंड को 11 समान भागों में विभाजित करेंगे। माना A, B, C, D, E, F, G, H, I, J समान भागों के बिन्दु हैं जो इस प्रकार हैं कि OA = AB = BC = ..... = JP रचना द्वारा OB,
OP का \(\frac{-2}{11}\) की वाँ भाग है । अतः B, \(\frac{-2}{11}\) को दर्शाता है। OE, OP का \(\frac{-5}{11}\) वाँ भाग है। अतःE, \(\frac{-5}{11}\) को दर्शाता है और OI, OP का \(\frac{-9}{11}\) वाँ भाग है। अतः I, \(\frac{-9}{11}\) को दर्शाता है।

प्रश्न 3.
ऐसी पाँच परिमेय संख्याएँ लिखिए जो 2 से छोटी हों।
हल:
2 से छोटी पाँच परिमेय संख्याएँ हैं|
1,\(\frac{1}{2}\), 0, -1, \(-\frac{1}{2}\)
(यहाँ और भी बहुत सी परिमेय संख्याएँ हो सकती हैं।)

प्रश्न 4.
\(\frac{-2}{5}\) और \(\frac{1}{2}\) के मध्य दस परिमेय संख्याएँ ज्ञात कीजिए।
हल:
सर्वप्रथम दी गई परिमेय संख्याओं के हर समान करेंगे
\(\frac{-2}{5}=\frac{-2 \times 4}{5 \times 4}=\frac{-8}{20}\)
और \(\frac{1}{2}=\frac{1 \times 10}{2 \times 10}=\frac{10}{20}\)

हम जानते हैं -8 < -7 < -6 ..... < 10
⇒ \(\frac{-8}{20}<\frac{-7}{20}<\frac{-6}{20}<\ldots<\frac{10}{20}\)

अतः हमारे पास 2 व 1 के मध्य निम्न दस परिमेय संख्याएँ हैं| 
\(\frac{-8}{20}<\frac{-7}{20}<\frac{-6}{20}<\ldots<\frac{10}{20}\) और \(\frac{2}{20}\)

प्रश्न 5.
(i) \(\frac{2}{3}\) और \(\frac{1}{2}\)
(ii) \(\frac{-3}{2}\) और \(\frac{5}{3}\)
(iii) \(\frac{1}{4}\) और \(\frac{1}{2}\) के मध्य पाँच परिमेय संख्याएँ ज्ञात कीजिए।
हल:
(i) \(\frac{2}{3}\) और \(\frac{1}{2}\) सर्वप्रथम दी गई परिमेय संख्याओं को समान हर वाली परिमेय संख्याओं में बदलेंगे

अत: है और 4 के बीच निम्न परिमेय संख्याएँ हैं \(\frac{41}{60}, \frac{42}{60}, \frac{43}{60}, \frac{44}{60}, \frac{45}{60}\)
[नोट-हम \(\frac{41}{60}\) से \(\frac{47}{60}\) के मध्य कोई पाँच परिमेय संख्याएँ ले सकते हैं।] 

(ii)  \(\frac{-3}{2}\) और \(\frac{5}{3}\) सर्वप्रथम दी गई परिमेय संख्याओं को समान हर वाली परिमेय संख्याओं में बदलेंगे

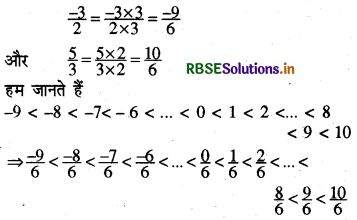
अतः \(\frac{-3}{2}\) और \(\frac{5}{3}\) के मध्य कोई पाँच परिमेय संख्याएँ निम्न प्रकार हैं
\(\frac{-8}{6}, \frac{-7}{6}, \frac{0}{6}, \frac{1}{6}\) और \(\frac{2}{6}\)

(iii) \(\frac{1}{4}\) और \(\frac{1}{2}\) सर्वप्रथम दी गई परिमेय संख्याओं को समान हर वाली परिमेय संख्याओं में बदलेंगे
\(\frac{1}{4}=\frac{1 \times 8}{4 \times 8}=\frac{8}{32}\)
और \(\frac{1}{2}=\frac{1 \times 16}{2 \times 16}=\frac{16}{32}\)
हम जानते हैं < 8 < 9 < 10 < 11 < 12 < 13 < 14 < 15 < 16
⇒ \(\frac{8}{32}<\frac{9}{32}<\frac{10}{32}<\ldots . .<\frac{15}{32}<\frac{16}{32}\)
अतः  \(\frac{1}{4}\) और \(\frac{1}{2}\) के मध्य कोई पाँच वांछित परिमेय संख्याएँ हैं
\(\frac{9}{32}, \frac{10}{32}, \frac{11}{32}, \frac{12}{32}\) और \(\frac{13}{32}\)

प्रश्न 6.
-2 से बड़ी पाँच परिमेय संख्याएँ लिखिए।
हल:
-2 से बड़ी पाँच परिमेय संख्याएँ होंगी
\(-\frac{3}{2},-1, \frac{-1}{2}, 0, \frac{1}{2}\)
[नोट- -2 से बड़ी बहुत सी परिमेय संख्याएँ हो सकती हैं]

प्रश्न 7. 
\(\frac{3}{5}\) और \(\frac{3}{4}\) के बीच में दस परिमेय संख्याएँ ज्ञात कीजिए।
हल:
सर्वप्रथम दी गई परिमेय संख्याओं को समान हर वाली परिमेय संख्याओं में बदलेंगे

अतः \(\frac{3}{5}\) और \(\frac{3}{4}\)  के बीच दस परिमेय संख्याएँ निम्न प्रकार होंगी
\(​​​​​​​\frac{61}{100}, \frac{62}{100}, \frac{63}{100}, \frac{64}{100}, \frac{65}{100}, \frac{66}{100}, \frac{67}{100}, \frac{68}{100}, \frac{69}{100}\) और \(\frac{70}{100}\)