RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.2

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.2 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 1 Rational Numbers Ex 1.2

Question 1.
Represent these numbers on the number line
(i) \(\frac{7}{4}\)
(ii) \(\frac{-5}{6}\)
Answer:
(i) For \(\frac{7}{4}\), we make 7 markings of distance \(\frac{1}{4}\) each on the right of zero and starting from 0. The seventh marking is \(\frac{7}{4}\).

Thus the point P represents \(\frac{7}{4}\) on the number line.

(ii) For \(\frac{-5}{6}\), we make 5 markings of distance \(\frac{1}{6}\) each on the left of zero and starting from 0. The fifth marking is The point P represents the rational number \(\frac{-5}{6}\).

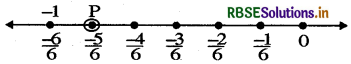
Question 2.
Represent \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on the number line.
Answer:
To represent \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on a number line, we draw a number line and mark a point P representing integeres - 1 on the left side of 0 on the number line.

We divide the segment OP into eleven equal parts. Let A, B, C, D, E, F, G, H, I, J be the points of division so that OA = AB = BC = ... = JP. By construction, OB is two-eleventh of OP so B represents \(\frac{-2}{11}\). OE is five-eleventh of OP so E represents \(\frac{-5}{11}\) and OI is nine-eleventh of OP so I represents \(\frac{-9}{11}\).

Question 3.
Write five rational numbers which are smaller than 2.
Answer:
Five rational numbers less than 2. may be taken as 1,1,0, -1, \(\frac{-1}{2}\)
(There can be many more such rational numbers)

Question 4.
Find ten rational numbers between \(\frac{-2}{5}\) and \(\frac{-1}{2}\).
Answer:
Converting the given rational numbers with the same denominators
\(\frac{-2}{5}=\frac{-2 \times 4}{5 \times 4}=\frac{-8}{20}\)
and \(\frac{1}{2}=\frac{1 \times 10}{2 \times 10}=\frac{10}{20}\)

We know that -8 < -7 < -6
⇒ \(\frac{-8}{20}<\frac{-7}{20}<\frac{-6}{20}<\ldots . .<\frac{10}{20}\)
Thus we have die following 10 rational numbers between \(\frac{-2}{5}\) and \(\frac{1}{2}\)
\(\frac{-7}{20}, \frac{-6}{20}, \frac{-5}{20}, \frac{-4}{20}, \frac{-3}{20}, \frac{-2}{20}, \frac{-1}{20}, 0, \frac{1}{20}\) and \(\frac{2}{20}\)

Question 5.
Find five rational numbers between.
(i) \(\frac{2}{3}\) and \(\frac{4}{5}\)
(ii) \(\frac{-3}{2}\) and \(\frac{5}{3}\)
(iii) \(\frac{1}{4}\) and \(\frac{1}{2} \)
Answer:
(i) Converting the given rational numbers with the same denominators.

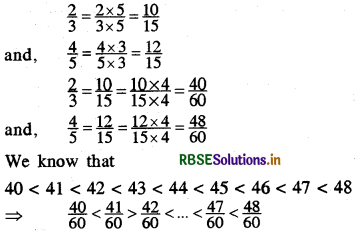
Hence, we have the following five rational numbers between \(\frac{2}{3}\) and \(\frac{4}{5}\)
\(\frac{41}{60}, \frac{42}{60}, \frac{43}{60}, \frac{44}{60}, \frac{45}{60}\)
[Note: We may take any five numbers given above from \(\frac{41}{60}\) to \(\frac{47}{60}\)]

(ii) \(\frac{-3}{2}\) and \(\frac{5}{3}\)
converting the given rational numbers with the same denominators.
\(\frac{-3}{2}=\frac{-3 \times 3}{2 \times 3}=\frac{-9}{6}\)
and \(\frac{5}{3}=\frac{5 \times 2}{3 \times 2}=\frac{10}{6}\)
We know that
\(\frac{-9}{6}<\frac{-8}{6}<\frac{-7}{6}<\frac{-6}{6}<\ldots<\frac{0}{6}<\frac{1}{6}<\frac{2}{6}<\ldots<\frac{8}{6}<\frac{9}{6}<\frac{10}{6}\)
Hence, we have the following five rational numbers between \(\frac{-3}{2}\) and \(\frac{5}{3}\).
\(\frac{-8}{6}, \frac{-7}{6}, \frac{0}{6}, \frac{1}{6}\) and \(\frac{2}{6}\)

(iii) \(\frac{1}{4}\) and \(\frac{1}{2}\)
converting the given rational numbers with the same denominators
\(\frac{1}{4}=\frac{1 \times 8}{4 \times 8}=\frac{8}{32}\)
and \(\frac{1}{2}=\frac{1 \times 16}{2 \times 16}=\frac{16}{32}\)

We know that
< 8 < 9 < 10 < 11 < 12 < 13 < 14 < 15 < 16
⇒ \(\frac{8}{32}<\frac{9}{32}<\frac{10}{32}<\ldots . .<\frac{15}{32}<\frac{16}{32}\)
Hence, we have the following five rational numbers between \(\frac{1}{4}\) and \(\frac{1}{2}\)
\(\frac{9}{32}, \frac{10}{32}, \frac{11}{32}, \frac{12}{32}\) and \(\frac{13}{32}\)

Question 6.
Write five rational numbers greater than - 2.
Answer:
Five rational numbers greater than - 2 may be taken as -\(\frac{3}{2}\),-1, \(\frac{-1}{2}\), 0, \(\frac{1}{2}\). [Note: There can be many more such rational numbers]

Question 7.
Find ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\).
Answer:
Converting the given rational numbers with the same denominators

Hence we have the following ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\).
\(\frac{61}{100}, \frac{62}{100}, \frac{63}{100}, \frac{64}{100}, \frac{65}{100}, \frac{66}{100}, \frac{67}{100}, \frac{68}{100}, \frac{69}{100}\) and \(\frac{70}{100}\)