RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1

Rajasthan Board RBSE Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1 Textbook Exercise Questions and Answers.

RBSE Class 8 Maths Solutions Chapter 1 Rational Numbers Ex 1.1

Question 1.
By using appropriate properties find.
(i) -$\frac{2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}$
Answer:

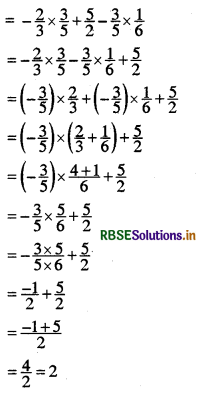
(ii) $\frac{2}{5} \times\left(-\frac{3}{7}\right)-\frac{1}{6} \times \frac{3}{2}+\frac{1}{14} \times \frac{2}{5}$
Answer:

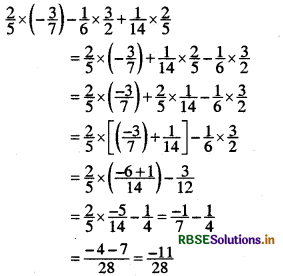
Question 2.
Write the additive inverse each of the following.
(i) $\frac{2}{8}$
Answer:
Additive inverse of $\frac{2}{8} = \frac{-2}{8}$

(ii) $\frac{-5}{9}$
Answer:
Additive inverse of $\left(\frac{-5}{9}\right)=\frac{5}{9}$

(iii) $\frac{-6}{-5}$
Answer:
Given $\frac{-6}{-5}$
Additive inverse of $\frac{6}{5}=\frac{-6}{5}$

(iv) $\frac{2}{-9}$
Answer:
Given $\frac{2}{-9}$
Additive inverse of $\frac{-2}{9}=\frac{2}{9}$

(v) $\frac{19}{-6}$
Answer:
Given $\frac{19}{-6}$
Additive inverse of $\frac{-19}{6}=\frac{19}{6}$

Question 3.
Verify that - (- x) = x for
(i) x = $\frac{11}{15}$
Answer:
x = $\frac{11}{15}$
∴ -(-x) = -$\left(-\frac{11}{15}\right)=\frac{11}{15}$ = x

(ii) x = $-\frac{13}{17}$
Answer:
∴ -(-x) = $-\left\{-\left(\frac{-13}{17}\right)\right\}=-\left(\frac{13}{17}\right)=-\frac{13}{17}$ = x

Question 4.
Find the multiplicative inverse of the following:
(i) -13
Answer:
Multiplicative inverse of (- 13) is
(-13)^-1 = $\frac{1}{-13}$

(ii) $\frac{-13}{19}$
Answer:
The multiplicative inverse of $\left(\frac{-13}{19}\right)$ is
$\left(\frac{-13}{19}\right)^{-1}=\frac{19}{-13}$

(iii) $\frac{1}{5}$
Answer:
The multiplicative inverse of $\left(\frac{1}{5}\right)$ is $\left(\frac{1}{5}\right)^{-1}$ = 5

(iv) $\frac{-5}{8} \times \frac{-3}{7}$
Answer:
Given $\frac{-5}{8} \times \frac{-3}{7}=\frac{-5 \times-3}{8 \times 7}=\frac{15}{56}$
Multiplicative inverse of $\frac{15}{56}$ is
$\frac{15}{56}$

(v) -1 × $\frac{-2}{5}$
Answer:
Given -1 × $\frac{-2}{5}=\frac{-1 \times-2}{5}=\frac{2}{5}$
Multiplicative inverse of $\frac{2}{5}$ is $\left(\frac{2}{5}\right)^{-1}=\frac{5}{2}$

(vi) -1
Answer:
Multiplicative inverse of -1
(-1)^-1 = $\frac{1}{-1}$ = -1

Question 5.
Name the property under multiplication used in each of the following:
(i) $\frac{-4}{5} \times 1=1 \times \frac{-4}{5}=-\frac{4}{5}$
Answer:
Existence of Multiplicative identity.

(ii) $-\frac{13}{17} \times \frac{-2}{7}=\frac{-2}{7} \times \frac{-13}{17}$
Answer:
Commutative property of multiplication.

(iii) $\frac{-19}{29} \times \frac{29}{-19}$ = 1
Answer:
Existence of multiplicative inverse.

Question 6.
Multiply $\frac{6}{13}$ by the reciprocal of $\frac{-7}{16}$
Answer:
$\frac{6}{13}$ × (the reciprocal of $\frac{-7}{16}$)
= $\frac{6}{13} \times\left(\frac{-7}{16}\right)^{-1}$
= $\frac{6}{13} \times \frac{16}{-7}=-\frac{96}{91}$

Question 7.
Tell what property allows you to compute $\frac{1}{3} \times\left(6 \times \frac{4}{3}\right)$ as $\left(\frac{1}{3} \times 6\right) \times \frac{4}{3}$
Answer:
Associative property of multiplication over rational numbers allows us to compute.

Question 8.
Is $\frac{8}{9}$ the multiplicative inverse of -1$\frac{8}{9}$? Why or why not?
Answer:
No, $\frac{8}{9}$ is not the multiplicative inverse of -1$\frac{8}{9}$. Because $\frac{8}{9} \times\left(-1 \frac{1}{8}\right)=\frac{8}{9} \times\left(\frac{-9}{8}\right)$
= -1 ≠ 1

Question 9.
Is 0.3 the multiplicative inverse of 3$\frac{1}{3}$? Why or why not?
Answer:
Yes, 0.3 is multiplicative inverse of -3$\frac{1}{3}$. Because 0.3 × 3$\frac{1}{3} = \frac{3}{10} \times \frac{10}{3}$ = 1

Question 10.
Write:
(i) The rational number that does not have a reciprocal.
Answer:
We know that there is no rational number which when multiplied with 0, gives 1. Therefore the rational number 0 has no reciprocal.

(ii) The rational numbers that are equal to their reciprocals.
Answer:
We know that the reciprocal of 1 is 1 and the reciprocal of - 1 is - 1. 1 and - 1 are the only reciprocal numbers which are their own reciprocals.

(iii) The rational number that is equal to its negative.
Answer:
The rational number 0 is equal to its negative.

Question 11.
Fill in the blanks.
(i) Zero has _______________     reciprocal.
Answer:
No

(ii) The numbers _______________    and    _______________ are their own, reciprocals.
Answer:
1, -1

(iii) The reciprocal of - 5 is _______________
Answer:
$\frac{-1}{5}$

(iv) Reciprocal of $\frac{1}{x}$ where x ≠ 0 is _______________
Answer:
x

(v) The product of two rational numbers is always a _______________
Answer:
rational number

(vi) The reciprocal of a positive rational number is _______________
Answer:
positive.