RBSE Solutions for Class 7 Maths Chapter 9 परिमेय संख्याएँ Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 9 परिमेय संख्याएँ Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 9 परिमेय संख्याएँ Intext Questions

(प्रयास कीजिए - पृष्ठ 191)

प्रश्न 1.
क्या संख्या $\frac{2}{-3}$ परिमेय संख्या है? इसके बारे में सोचिए।
हल:
हाँ, यह ऋणात्मक परिमेय संख्या है।

प्रश्न 2.
दस परिमेय संख्याओं की एक सूची बनाइए।
हल:
दस परिमेय संख्याओं की सूची इस प्रकार है :
$\frac{1}{3}, \frac{2}{3}, \frac{4}{7}, \frac{5}{9}, \frac{-7}{-9}, \frac{3}{-7}, \frac{-4}{5}, \frac{5}{9}, \frac{11}{13}$ और $\frac{21}{27}$

 

(प्रयास कीजिए - पृष्ठ 192-I)

प्रश्न 1.
रिक्त स्थानों को भरिए :

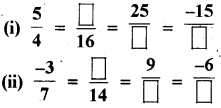
हल:
(i) बॉक्स को भरने के लिए $\frac{5}{4}$ को हमें ऐसी परिमेय संख्या के रूप में व्यक्त करना होगा, जिसका हर 16 हो। इसके लिए हमें ऐसा पूर्णांक प्राप्त करना होगा जो 4 से गुणा करने पर 16 देता हो।
स्पष्ट है ऐसा पूर्णांक 16 ÷ 4 = 4
अंश व हर दोनों को 4 से गुणा करने पर

(ii) बॉक्स को भरने के लिए $\frac{-3}{7}$ को 14 हर वाली समतुल्य परिमेय संख्या में बदलना होगा।
अतः $\frac{-3}{7}$ के हर व अंश में 2 से गुणा करने पर

(प्रयास कीजिए - पृष्ठ 192-II)

प्रश्न 1.
क्या 5 एक धनात्मक परिमेय संख्या है?
हल:
हम जानते है कि 5 = $\frac{5}{1}$ जहाँ 5 और 1 दोनों धनात्मक हैं।
इसलिए 5 एक धनात्मक परिमेय संख्या है।

प्रश्न 2.
पाँच और धनात्मक परिमेय संख्याएँ लिखिए।
हल:
पाँच धनात्मक परिमेय संख्याएँ इस प्रकार हैं :
$\frac{1}{3}, \frac{3}{2}, \frac{3}{4}, \frac{11}{17}$ और $\frac{23}{27}$

(प्रयास कीजिए - पृष्ठ 192-III)

प्रश्न 1.
क्या - 8 एक ऋणात्मक परिमेय संख्या
हल:
हम जानते हैं कि - 8 = $\frac{-8}{1}$ जहाँ - 8 ऋणात्मक और 1 धनात्मक है।
∴ - 8 एक ऋणात्मक परिमेय संख्या है।

प्रश्न 2.
पाँच और ऋणात्मक परिमेय संख्याएँ लिखिए।
हल:
पाँच ऋणात्मक परिमेय संख्याएँ इस प्रकार हैं :
$\frac{-1}{3}, \frac{-3}{2}, \frac{3}{-4}, \frac{-11}{17}$ और $\frac{-23}{27}$

(प्रयास कीजिए - पृष्ठ 193)

प्रश्न 1.
निम्नलिखित में से कौनसी संख्याएँ ऋणात्मक परिमेय संख्याएँ हैं?
(i) $\frac{-2}{3}$
हल:
$\frac{-2}{3}$ में हर व अंश में विपरीत चिह्न के हैं। इसलिए $\frac{-2}{3}$ एक ऋणात्मक परिमेय संख्या है।

(ii) $\frac{5}{7}$
हल:
$\frac{5}{7}$ में हर और अंश दोनों समान चिह्न के हैं। इसलिए $\frac{5}{7}$, ऋणात्मक परिमेय संख्या नहीं है।

(iii) $\frac{3}{-5}$
हल:
$\frac{3}{-5}$ में अंश व हर विपरीत चिह्न के हैं। इसलिए $\frac{3}{-5}$ ऋणात्मक परिमेय संख्या है।

(iv) 0
हल:
शून्य संख्या न धनात्मक है और न ही ऋणात्मक है।

(v) $\frac{6}{11}$
हल:
$\frac{6}{11}$ में, अंश व हर समान चिह्न के हैं। इसलिए $\frac{6}{11}$ ऋणात्मक परिमेय संख्या नहीं है।

(vi) $\frac{-2}{-9}$
हल:
$\frac{-2}{-9}$ में, हर व अंश समान चिह्न के हैं। इसलिए $\frac{-2}{-9}$ ऋणात्मक परिमेय संख्या नहीं है।

(प्रयास कीजिए - पृष्ठ 196)

प्रश्न 1.
मानक रूप ज्ञात कीजिए :
(i) $\frac{-18}{45}$
हल:
$\frac{-18}{45}$ के लिए :
परिमेय संख्या $\frac{-18}{45}$ का हर धनात्मक है। इसे मानक रूप में व्यक्त करने के लिए हम इसके अंश व हर को 18 और 45 के म.स. से भाग करते हैं। 18 और 45 का म.स. 9 है।
$\frac{-18}{45}$ के अंश व हर को 9 से भाग देने पर
$\frac{-18}{45}=\frac{(-18) \div 9}{45 \div 9}=\frac{-2}{9}$
अतः $\frac{-18}{45}$ का मानक रूप में है।

(ii) $\frac{-12}{18}$ के लिए :
परिमेय संख्या का हर धनात्मक है।
इसे मानक रूप में व्यक्त करने के लिए अंश व हर को 12 व 18 के म.स. से भाग देने पर
12 व 18 का म.स. 6 है।
$\frac{12}{18}$ के अंश व हर को 6 से भाग देने पर
$\frac{-12}{18}=\frac{(-12) \div 6}{18 \div 6}=\frac{-2}{3}$
इस प्रकार, $\frac{-12}{18}$ का मानक रूप $\frac{-2}{3}$ में है।

(प्रयास कीजिए - पृष्ठ 198)

प्रश्न 1.
$\frac{-5}{7}$ और $\frac{-3}{8}$ के बीच में पाँच परिमेय संख्याएँ ज्ञात कीजिए।
हल:

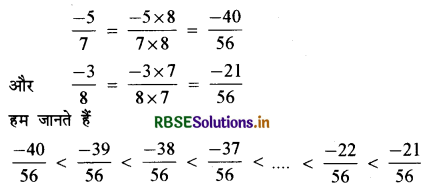
इसलिए, $\frac{-5}{7}$ और $\frac{-3}{8}$ के बीच कोई पाँच परिमेय संख्याएँ इस प्रकार
$\frac{-39}{56}, \frac{-38}{56}, \frac{-37}{56}, \frac{-36}{56}$ और $\frac{-35}{56}$

(प्रयास कीजिए - पृष्ठ 201)

प्रश्न 1.
$\frac{-13}{7 .}+\frac{6}{7}$ तथा $\frac{19}{5}+\left(\frac{-7}{5}\right)$ ज्ञात कीजिए।
हल:

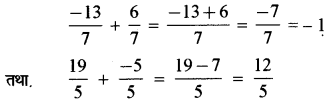
(प्रयास कीजिए - पृष्ठ 202-I)

प्रश्न 1.
ज्ञात कीजिए :
(i) $\frac{-3}{7}+\frac{2}{3}$
हल:
$\frac{-3}{7}+\frac{2}{3}$
दोनों संख्याओं का हर धनात्मक है। 7 और 3 का ल.स. = 21 होगा।

(ii) $\frac{-5}{6}+\frac{-3}{11}$
हल:
दोनों संख्याओं का हर धनात्मक है। 6 और 11 का ल.स. = 66 है।

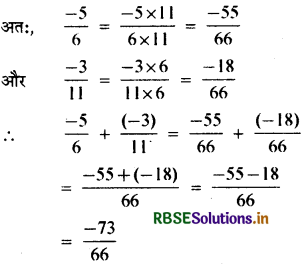
(प्रयास कीजिए - पृष्ठ 202-17)

प्रश्न 1.
$\frac{-3}{9}, \frac{-9}{11}$ और $\frac{5}{7}$ के योज्य प्रतिलोम क्या
हल:
$\frac{-3}{9}$ का योज्य प्रतिलोम $\frac{-3}{9}=-\left(\frac{-3}{9}\right)=\frac{3}{9}$
$\frac{-9}{11}$ का योज्य प्रतिलोम = $-\left(\frac{-9}{11}\right)=\frac{9}{11}$ है।
$\frac{5}{7}$ का योज्य प्रतिलोम = $-\left(\frac{5}{7}\right)=\frac{-5}{7}$ है।

(प्रयास कीजिए - पृष्ठ 203)

प्रश्न 1.
ज्ञात कीजिए :
(i) $\frac{7}{9}-\frac{2}{5}$
हल:

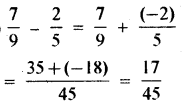
(ii) 2$\frac{1}{5}-\frac{(-1)}{3}$
हल:

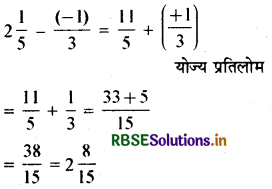
(प्रयास कीजिए - पृष्ठ 204-I)

प्रश्न 1.
निम्नलिखित गुणनफल क्या होंगे?
(i) $\frac{-3}{5}$ × 7
हल:
$\frac{-3}{5}$ × 7 = $\frac{(-3) \times 7}{5}=\frac{-21}{5}$

(ii) $\frac{-6}{5}$ × (-2)
हल:
$\frac{-6}{5}$ × (-2) = $\frac{(-6) \times(-2)}{5}=\frac{12}{5}$

(प्रयास कीजिए - पृष्ठ 204-II)

प्रश्न 1.
ज्ञात कीजिए :
(i) $\frac{-3}{4} \times \frac{1}{7}$
हल:
$\frac{-3}{4} \times \frac{1}{7}=\frac{(-3) \times 1}{4 \times 7}=\frac{-3}{28}$

(ii) $\frac{2}{3} \times \frac{-5}{9}$
हल:
$\frac{2}{3} \times \frac{-5}{9}=\frac{2 \times(-5)}{3 \times 9}=\frac{-10}{27}$

(प्रयास कीजिए - पृष्ठ 205-I)

प्रश्न 1.
$\frac{-6}{11}, \frac{-8}{5}$ के व्युत्क्रम क्या होंगे?
हल:
$\frac{-6}{11}$ का व्युत्क्रम $\frac{11}{-6}$, और $\frac{-8}{5}$ का व्युत्क्रम $\frac{5}{-8}$

(प्रयास कीजिए - पृष्ठ 205-II)

प्रश्न 1.
ज्ञात कीजिए :
(i) $\frac{2}{3} \times \frac{-7}{8}$
हल:
$\frac{2}{3} \times \frac{-7}{8}=\frac{2 \times(-7)}{3 \times 8}$
= $\frac{-14}{24}=\frac{-7}{12}$

(ii) $\frac{-6}{7} \times \frac{5}{7}$
हल:
$\frac{-6}{7} \times \frac{5}{7}=\frac{(-6) \times 5}{7 \times 7}=\frac{-30}{49}$