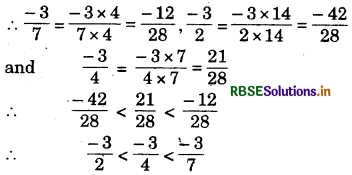RBSE Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.1

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.1 Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 9 Rational Numbers Ex 9.1

Question 1.
List five rational numbers between:
(i) - 1 and 0
Answer:
Write -1 and 0 as rational numbers with denominator 6.
-1 × $\frac{6}{6}=\frac{-6}{6}$ and 0 × $\frac{6}{6}=\frac{0}{6}$
Five rational numbers between $\frac{0}{6}$ and $\frac{-6}{6}$ are $\frac{-1}{6}, \frac{-2}{6}, \frac{-3}{6}, \frac{-4}{6}$ and$\frac{-5}{6}$

(ii) - 2 and - 1
Answer:
Write - 2 and - 1 as rational numbers with denominator 6.
2 × $\frac{6}{6}=\frac{-12}{6}$ and -1 × $\frac{6}{6}=\frac{-6}{6}$
Five rational numbers between $\frac{-6}{6}$ and $\frac{-12}{6}$ are $\frac{-7}{6}, \frac{-8}{6}, \frac{-9}{6}, \frac{-10}{6}$and $\frac{-11}{6}$

(iii) $-\frac{4}{5}$ and $-\frac{2}{3}$
Answer:
LCM of 5 and 3 = 15
Write $\frac{-4}{5}$ and $-\frac{2}{3}$ with denominator 15.
$\frac{-4}{5} \times \frac{3}{3}=\frac{-12}{15}$ and $\frac{-2}{3} \times \frac{5}{5}=\frac{-10}{15}$

 Now multiply $\frac{-12}{15}$ and $\frac{-10}{15}$ with$\frac{10}{10}$ to get 5 rational numbers
$\frac{-12}{15} \times \frac{10}{10}=\frac{-120}{150}$ and $\frac{-10}{15} \times \frac{10}{10}=\frac{-100}{150}$
Five rational numbers between $\frac{-4}{5}$ and $\frac{-2}{3}$ are $\frac{-119}{150}, \frac{-118}{150}, \frac{-117}{150}, \frac{-116}{150}, \frac{-115}{150}$

(iv) $-\frac{1}{2}$ and $\frac{2}{3}$
Answer:
LCM of 2 and 3 = 6
Write $-\frac{1}{2}$ and $\frac{2}{3}$ with denominator 6.
$\frac{1}{2} \times \frac{3}{3}=\frac{3}{6}$and $\frac{2}{3} \times \frac{2}{2}=\frac{4}{6}$

Multiply $\frac{3}{6}$and $\frac{4}{6}$ with $\frac{10}{10}$ to get 5 rational numbers.
$\frac{3}{6} \times \frac{10}{10}=\frac{30}{60}$ and$\frac{4}{6} \times \frac{10}{10}=\frac{40}{60}$
Five rational numbers between $\frac{1}{2}$ and $\frac{2}{3}$ are $\frac{31}{60}, \frac{32}{60}, \frac{33}{60}, \frac{34}{60}, \frac{35}{60}$

Question 2.
Write four more rational numbers in each of the following patterns :
(i) $\frac{-3}{5}, \frac{-6}{10}, \frac{-9}{15}, \frac{-12}{20}$ ..........................
Answer:
$\frac{-3}{5}, \frac{-6}{10}, \frac{-9}{15}, \frac{-12}{20}$ ..........................
Next four rational numbers are
$\frac{-15}{25}, \frac{-18}{30}, \frac{-21}{35}, \frac{-24}{40}$

(ii) $\frac{-1}{4}, \frac{-2}{8}, \frac{-3}{12}$ ..............................
Answer:
$\frac{-1}{4}, \frac{-2}{8}, \frac{-3}{12}$ ..............................
Next four rational numbers are
$\frac{-4}{16}, \frac{-5}{20}, \frac{-6}{24}, \frac{-7}{28}$

(iii) $\frac{-1}{6}, \frac{2}{-12}, \frac{3}{-18}, \frac{4}{-24}$ ..........................
Answer:
$\frac{-1}{6}, \frac{2}{-12}, \frac{3}{-18}, \frac{4}{-24}$..........................
Next four rational numbers are
$\frac{-5}{30}, \frac{-6}{36}, \frac{-7}{42}, \frac{-8}{-48}$

(iv) $\frac{-2}{3}, \frac{2}{-3}, \frac{4}{-6}, \frac{6}{-9}$ .............................
Answer:
$\frac{-2}{3}, \frac{2}{-3}, \frac{4}{-6}, \frac{6}{-9}$ .............................
Next four rational numbers are
$\frac{8}{-12}, \frac{10}{-15}, \frac{12}{-18}, \frac{14}{-21}$

Question 3.
Give four rational numbers equivalent to:
(i) $\frac{-2}{7}$
Answer:
$\frac{-2}{7}$
$\frac{-2}{7} \times \frac{2}{2}=\frac{-4}{14} ; \frac{-2}{7} \times \frac{3}{3}=\frac{-6}{21}$
$\frac{-2}{7} \times \frac{4}{4}=\frac{-8}{28} ; \frac{-2}{7} \times \frac{5}{5}=\frac{-10}{35}$
Four Rational Numbers equivalent to $\frac{-2}{7}$ are $\frac{-4}{14}, \frac{-6}{21}, \frac{-8}{28}, \frac{-10}{35}$

(ii) $\frac{5}{-3}$
Answer:

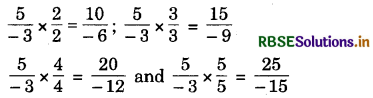
Four Rational Numbers equivalent to $\frac{5}{-3}$ are $\frac{10}{-6}, \frac{15}{9}, \frac{20}{-12}$ and $\frac{25}{-15}$

(iii) $\frac{4}{9}$
Answer:

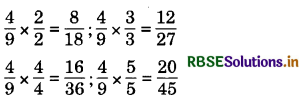
Four Rational Numbers equivalent to are $\frac{8}{18}, \frac{12}{27}, \frac{16}{36}, \frac{20}{45}$

Question 4.
Draw the number line and represent the following rational numbers on it:
(i) $\frac{3}{4}$
Answer:

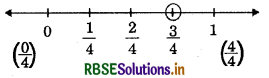
(ii) $\frac{-5}{8}$
Answer:

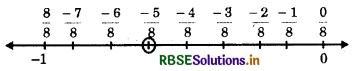
(iii) $\frac{-7}{4}$
Answer:

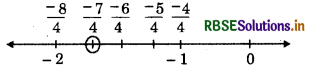
(iv) $\frac{7}{8}$
Answer:

Question 5.
The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP *= PQ = QB. Name the rational numbers represented by P, Q, R and S.

Answer:
Here, AP = PQ = QB, between 2 and 3 there are 3 equal parts and between - 2 and - 1 there are 3 equal parts.
∴ P represents = 2 + $\frac{1}{3}=\frac{6+1}{3}=\frac{7}{3}$
= 2$\frac{1}{3}$

Q represents = 2 + $\frac{2}{3}=\frac{6+2}{3}=\frac{8}{3} = 2 \frac{2}{3}$
R represent = - 1 - $\frac{1}{3}=\frac{-3-1}{3}=\frac{-4}{3} = -1 \frac{1}{3}$
S represent = -1 - $\frac{2}{3}=\frac{-3-2}{3}=\frac{-5}{3} = -1 \frac{2}{3}$

Question 6.
Which of the following pairs represent the same rational number?
(i) $\frac{-7}{21}$ and $\frac{3}{9}$
Answer:
$\frac{-7}{21}$ and $\frac{3}{9}$
Here, $\frac{-7}{21}$ is a negative rational number and $\frac{3}{9}$ is a positive rational number,
∴ $\frac{-7}{21} \neq \frac{3}{9}$

(ii) $\frac{-16}{20}$ and $\frac{20}{-25}$
Answer:
$\frac{-16}{20}$ and $\frac{20}{-25}$
$\frac{-16 \div 4}{20 \div 4}=\frac{-4}{5}=\frac{-4}{5}$ and $\frac{20 \div 5}{-25 \div 5}=\frac{4}{-5}=-\frac{4}{5}$
∴ $\frac{-16}{20}=\frac{20}{-25}$
Thus, $\frac{-16}{20}$ and $\frac{20}{-25}$ represent the same rational numbers.

(iii) $\frac{-2}{-3}$ and $\frac{2}{3}$
Answer:
$\frac{(-2) \div(-1)}{(-3) \div(-1)}=\frac{2}{3}$
∴ $\frac{-2}{-3}=\frac{2}{3}$
Thus, $\frac{-2}{-3}$ and $\frac{2}{3}$ represent the same rational numbers.

(iv) $\frac{-3}{5}$ and $\frac{-12}{20}$
Answer:
$\frac{-3}{5}=\frac{-3}{5} \times \frac{4}{4}=\frac{-12}{20}$
∴ $\frac{-3}{5}=\frac{-12}{20}$
Thus, $\frac{-3}{5}$ and $\frac{-12}{20}$ represent the same rational numbers.

(v) $\frac{8}{-5}$ and $\frac{-24}{15}$
Answer:
$\frac{8}{-5}=\frac{8}{-5} \times \frac{3}{3}=\frac{24}{-15}=\frac{-24}{15}$
∴ $\frac{8}{-5}=\frac{-24}{15}$
Thus, $\frac{8}{-5}$ and $\frac{-24}{15}$ represent the same rational numbers.

(vi) $\frac{1}{3}$ and $\frac{-1}{9}$
Answer:
Here, $\frac{1}{3}$ is a positive integer and $\frac{-1}{9}$ is a negative integer, so $\frac{1}{3} \neq \frac{-1}{9}$

(vii) $\frac{-5}{-9}$ and $\frac{5}{-9}$
Answer:
$\frac{-5}{-9}=\frac{-5 \div(-1)}{-9 \div(-1)}=\frac{5}{9}$
Here, $\frac{-5}{-9}$ is a positive integer and $\frac{5}{-9}$ is a negative integer, so $\frac{-5}{-9} \neq  \frac{5}{-9}$

Question 7.
Rewrite the following rational number in the simplest form :
(i) $\frac{-8}{6}$
Answer:
$\frac{-8}{6}$
∵ HCF of 8 and 6 is 2
∴$\frac{-8}{6}=\frac{-8 \div 2}{6 \div 2}=\frac{-4}{3}$
Simplest form of $\frac{-8}{6}$ is $\frac{-4}{3}$

(ii) $\frac{25}{45}$
Answer:
$\frac{25}{45}$
∵ HCF of 25 and 45 is 5
∴ $\frac{25}{45}=\frac{25 \div 5}{45 \div 5}=\frac{5}{9}$
Simplest form of $\frac{25}{45}$ is $\frac{5}{9}$

(iii) $\frac{-44}{72}$
Answer:
$\frac{-44}{72}$
∵ HCF of 44 and 72 is 4.
∴ $\frac{-44}{72}=\frac{-44 \div 4}{72 \div 4}=\frac{-11}{18}$
Simplest form of $\frac{-44}{72}$ is $\frac{-11}{18}$

(iv) $\frac{-8}{10}$
Answer:
$\frac{-8}{10}$
∵ HCF of 8 and 10 is 2.
∴ $\frac{-44}{72}=\frac{-44 \div 4}{72 \div 4}=\frac{-11}{18}$
Simplest form of $\frac{-44}{72}$ is $\frac{-11}{18}$

Question 8.
Fill in the blanks with the correct symbol out of >, < and = :
(i) $\frac{-5}{7}$ _________ $\frac{2}{3}$
Answer:
Since $\frac{-5}{7}$ is negative rational number and $\frac{2}{3}$ is a positive rational number.

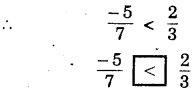
(ii) $\frac{-4}{5}$ ___________ $\frac{-5}{7}$
Answer:
LCM of 5 and 7 = 35

(iii) $\frac{-7}{8}$ _________ $\frac{14}{-16}$
Answer:
LCM of 8 and 16 = 16

(iv) $\frac{-8}{5}$ _________ $\frac{-7}{4}$
Answer:
LCM of 5 and 4 = 20

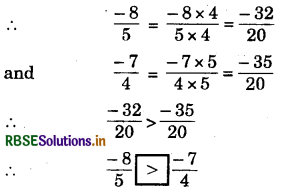
(v) $\frac{1}{-3}$ _________ $\frac{-1}{4}$
Answer:
LCM of 3 and 4 = 12

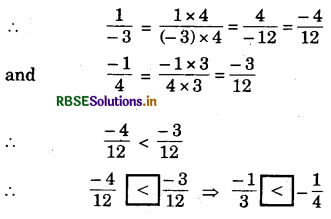
(vi) $\frac{5}{-11}$ _________ $\frac{-5}{11}$
Answer:

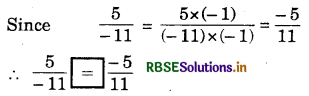
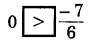
(vii) 0 _________ $\frac{-7}{6}$
Answer:
Since 0 is greater than every negative number.

Question 9.
Which is greater in each of the following:
(i) $\frac{2}{3}, \frac{5}{2}$
Answer:
∴ LCM of 3 and 2 = 6

Thus, $\frac{5}{2}$ is greater rational number.

(ii) $\frac{-5}{6}, \frac{-4}{3}$
Answer:
∴ LCM of 6 and 3 = 6

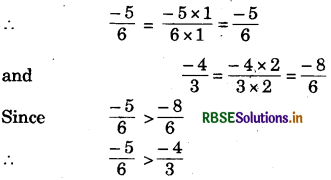
(iii) $\frac{-3}{4}, \frac{2}{-3}$
Answer:
∴ LCM of 4 and 3 = 12

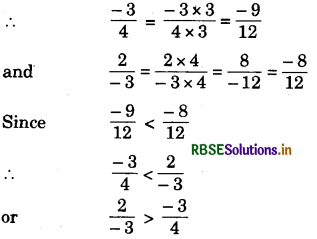
Thus, $\frac{2}{-3}$ is greater rational number.

(iv) $\frac{-1}{4}$, $\frac{1}{4}$
Answer:
Since a positive rational number is always greater than a negative rational number.
∴ $\frac{1}{4}>\frac{-1}{4}$
Thus, $\frac{1}{4}$ is greater rational number.

(v) -3$\frac{2}{7}$, -3$\frac{4}{5}$
Answer:

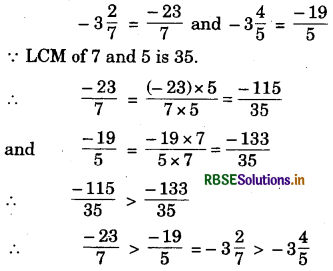
Thus, -3$\frac{2}{7}$ is greater rational number.

Question 10.
Write the following rational numbers in ascending order:
(i) $\frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5}$
Answer:
Since (- 3) < (- 2) < (- 1)
∴ $\frac{-3}{5}<\frac{-2}{5}<\frac{-1}{5}$
Ascending order of given rational number is $\frac{-3}{5}<\frac{-2}{5}<\frac{-1}{5}$

(ii) $\frac{-1}{3}, \frac{-2}{9}, \frac{-4}{3}$
Answer:
Since LCM of 3, 9 and 3 is 9.

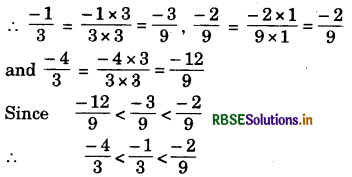
(iii) $\frac{-3}{7}, \frac{-3}{2}, \frac{-3}{4}$
Answer:
∴ LCM of 7, 2 and 4 is 28