RBSE Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 7 Congruence of Triangles Intext Questions

(Think, Discuss and Write - Page 137)

Question 1.
When two triangles say ABC and PQR are given there are, in all, six possible matchings or correspondence. Two of them are :
(i) ABC ↔ PQR and
(ii) ABC ↔ QRP
Find the other four correspondences by using two cutouts of triangles. Will all these correspondences lead to congruence? Think about it.
Answer:
The other four correspondence are:

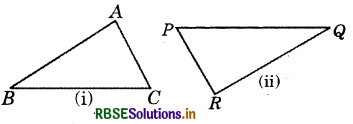
(i) ABC ↔ PRQ
(ii) ABC ↔ QPR
(iii) ABC ↔ RPQ 
(iv) ABC ↔ RQP

(Try These - Page 140 - 141)

Question 1.
In figures lengths of the sides of the triangles are indicated. By applying he SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form :

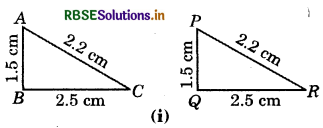
Answer:
Here, \(\overline{A B}=\overline{P Q}\) (= 1.5 cm)
\(\overline{B C}=\overline{Q R}\) (=2.5 cm)
\(\overline{C A}=\overline{R P}\) (= 2.2 cm)
∴ The three sides of a triangle ABC are equal to three sides of triangle PQR. So, by SSS congruence rule, the two triangles are congruent. From the above equalities relations, we see that
A ↔ P, B ↔ Q and C ↔ R 
So, we have ΔABC ≅ ΔPQR

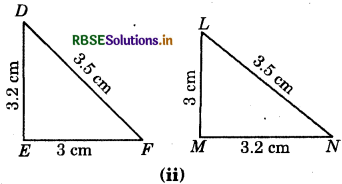
Answer:
Here, \(\overline{E D}=\overline{M N}\) (= 3.2 cm)
\(\overline{D F}=\overline{L N}\) (= 3.5 cm)
\(\overline{F E}=\overline{L M}\) (=3 cm)
∴ The three sides of ΔEDF are equal to three sides of ΔMNL. So, by SSS congruence rule, the triangles EDF and MNL are congruent.
Also, from above equality relations, we see that
E ↔ M, D ↔ N and F ↔ L
So, we have ΔEDF ≅ ΔMNL

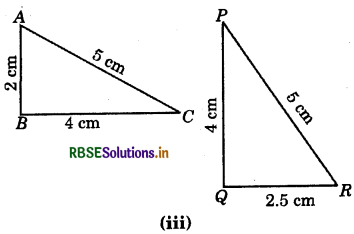
Answer:
Here, AC = PR (= 5 cm)
BC = PQ (= 5 cm)
AB ≠ QR (= 5 cm)
∴ The three sides of triangle ABC is not equal to three sides of triangle PQR.
ΔABC and ΔPQR are not congruent.

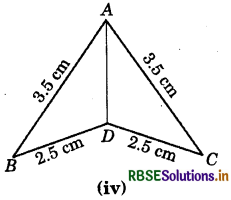
Answer:
Here, AB = AC (= 3.5 cm) BD = DC (= 2.5 cm) AD = AD (Common in both triangles) 
∴ The sides of triangle ABD are equal to three sides of triangle ACD. So, by SSS congruence rule, AABD and AACD are congruent.
A ↔ A, B ↔ C and D ↔ D 
ΔABD ≅ ΔACD.

Question 2.
In fig. AB = AC and D is the mid-point of BC.

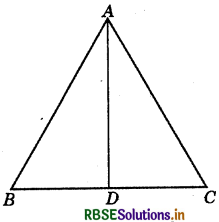
(i) State the three pairs of equal parts in ΔADB and ΔADC.
(ii) Is ΔADB ≅ ΔADC? Give reasons.
(iii) Is ∠B = ∠C? Why?
Answer:
(i) Given AB = AC
AD = AD (Common side) 
BD = CD as D is the mid-point of BC.

(ii) From (i), we see that three sides of ΔABD is equal to three sides of ΔACD.
So, by SSS congruence rule, the ΔABD and ΔACD are congruent.
Also A ↔ A, B ↔ Cand D ↔ D
∴ ΔABD ≅ ΔACD

(iii) Yes ∠B = ∠C. Since ∠B and ∠C are corresponding parts of congruent triangles.

Question 3.
In the given fig., AC = BD and AD = BC.
Which of the following statements is meaningfully written? 

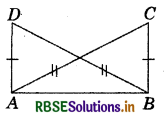
(i) ΔABC ≅ ΔABD
(ii) ΔABC ≅ ΔBAD
Answer:
The statement (ii) is ΔABC ≅ ΔBAD is meaningfully written.

(Think, Discuss and Write - Page 141)

Question 1.
ABC is an isosceles triangle with AB = AC (see figure). Take a trace copy of, ΔABC and also name it as ΔABC.

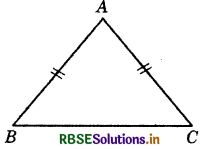
(i) State the three pairs of equal parts in ΔABC and ΔACB.
Answer:
AB = AC, BC = CB, AC = AB

(ii) Is ΔABC ≅ ΔACB? Why or why not?
Answer:
Yes, because the three sides of ΔABC and ΔACB are equal.
So, by SSS congruence rule, the two tr angles are congruent.
Also A ↔ A, B ↔ C and C ↔ B 
ΔABC ≅ ΔACB

(iii) Is ∠B = ∠C? Why or why not?
Answer:
Yes, ∠B = ∠C (Corresponding parts of congruent triangles)

(Try These - Page 143-144)

Question 1.
Which angle is included between the sides \(\overline{D E}\) and \(\overline{E F}\) of ΔDEF?
Answer:
∠DEF is included between the sides \(\overline{D E}\) and \(\overline{E F}\)
 
Question 2.
By applying SAS congruence rule, you want to establish that ΔPQR ≅ ΔFED. It is given that PQ = FE and RP = DF. What additional information is needed to establish the congruence?
Answer:
We need to know about the equal angles in ΔPQR and ΔFED, i.e. we need to establish ∠QPR = ∠EFD.

Question 3.
In figures, measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.

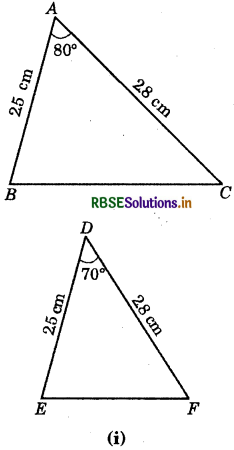
Answer:
AB = DE (= 2.5 cm)
AC = DF (= 2.8 cm)
But ∠BAC ≠ ∠EDF (Included angle)
So, ΔBAC and ΔEDF are not congruent.

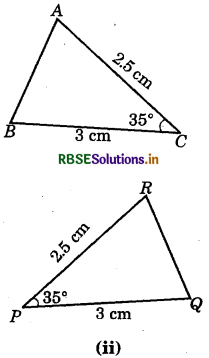
Answer:
CB = QP (=3 cm)
CA =PR (= 2.5 cm)
Also ∠BCA = ∠QPR (Included angle)
Also C ↔ P, B ↔ Q and A ↔ R
∴ ΔBCA ≅ ΔQPR
(By SAS congruence rule)

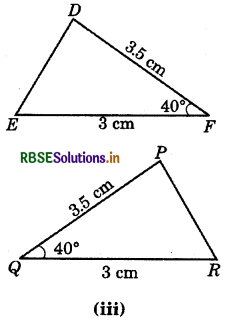
Answer:
FD = QP (= 3.5 cm)
FE = QR (= 3 cm)
Also ∠PQR = ∠DFE (Included angle) 
Also F ↔ Q, E ↔ R and D ↔ P
ΔEDF ≅ ΔRPQ
(By SAS congruence rule)

(iv) SR = QP (= 3.5 cm)
RP = PR (Common in both triangles) 
Also ∠QPR = ∠SRP (Included angle) 
Also S ↔ Q, R ↔ P and P ↔ R 
ΔSRP ≅ ΔQPR
(By SAS congruence rule)

Question 4.
In the given fig. \(\overline{A B}\) and \(\overline{C D}\) bisect each other at O.
(i) State the three pairs of equal parts in two triangles AOC and BOD.
(ii) Which of the following statements are true?

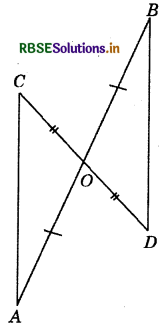
(a) ΔAOC ≅ ΔDOB
(b) ΔAOC ≅ ΔBOD
Answer:
(i) OA = OB, OC = OD
and ∠AOC = ∠BOD

(ii) The statement 
(b) AAOC = ABOD is true.

(Try These - Page 145-146)

Question 1.
What is the side included between the angles M and N of ΔMNP?
Answer:
MAT.

Question 2.
You want to establish ΔDEF ≅ ΔMNP, using the ASA congruence rule. You are given that ∠D = ∠M and ∠F = ∠P. What information is needed to establish the congruence? (Draw a rough figure and then try!)
Answer:
\(\overline{D F}=\overline{M P}\)

 
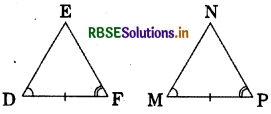
Question 3.
In the given figures, measures of some parts are indicated. By applying ASA congruence rule, state which pairs of triangles are congruent. In case of congruence, write the result in symbolic form.

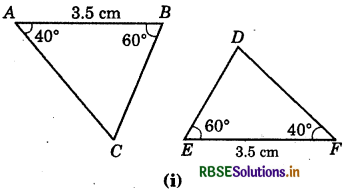
Answer:
\(\overline{A B}=\overline{F E}\) (= 3.5 cm)
∠ABC = ∠FED (= 60°)
∠CAB = ∠DFE (= 40°)
∴ ΔABC ≅ ΔFED
(By ASA congruence rule)

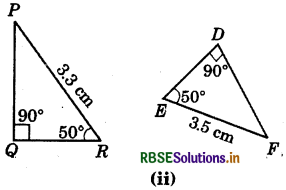
Answer:
∠PQR = ∠FDE (= 90°)
∠QRP = ∠DEF (= 50°)
But PR ≠ EF
ΔPQR is not congruent to ΔFDE.

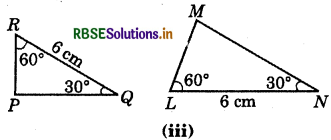
Answer:
\(\overline{P Q}=\overline{L N}\) (=6 cm)
∠PQR = ∠MNL (= 60°)
∠PRQ = ∠MLN (= 30°)
ΔPQR ≅ ΔMNL
(By ASA congruence rule)

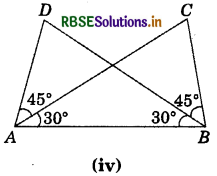
Answer:
AB = BA
(Common to both triangles)
∠ABD = ∠CAB
∠DAB = ∠CBA 
ΔABC ≅ ΔBAD
(By ASA congruence rule)

Question 4.
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by ASA congruence rule. In case of congruence, write it in symbolic form.
ΔDEF
(i) ∠D = 60°, ∠F = 80°, DF = 5 cm
(ii) ∠D = 60°, ∠F = 80°, DF = 6 cm
(iii) ∠E = 80°, ∠F = 30°, EF = 5 cm
ΔPQR
(i) ∠Q = 60°, ∠R = 80°, QR = 5 cm
(ii) ∠Q = 60°, ∠R = 80°, QP = 6 cm
(iii) ∠P = 80°, PQ = 5 cm, ∠R = 30°
Answer:
(i) ΔDFE ≅ ΔQRP
(ii) ΔDEF is not congruent to ΔPQR.
(iii) ΔDEF is not congruent to ΔPQR.

Question 5.
In figure, ray AZ bisects ∠DAB as well as ∠DCB.

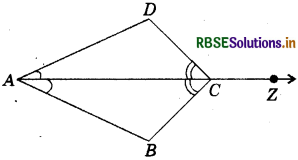
(i) State the three pairs of equal parts in triangles BAC and DAC.
Answer:
∠BAG = ∠DAC
∠BCA = ∠DCA
AC = AC

(ii) Is ΔBAC ≅ ΔDAC? Give reasons.
Answer:
Yes, ABAC and ADAC are congruent by ASA congruence rule.

(iii) Is AB - AD? Justify your answer.
Answer:
Yes, AB = AD since corresponding parts of congruent triangles are equal.

(iv) Is CD = CB? Give reasons.
Answer:
Yes, CD = CB corresponding parts of congruent triangles are equal.

(Try These - Page 148)

Question 1.
In the given figures, measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form.

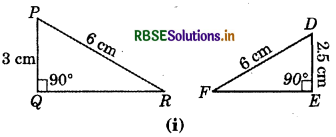
Answer:
Here, ∠PQR = ∠DEF(= 90°)
Hypotenuse PR= Hypotenuse DF (= 6 cm)
Side PQ ≠ Side DE
So, the triangle PQR and DEF are not congruent.

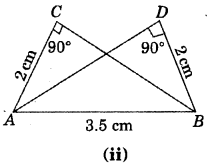
Answer:
Here, ∠ACB = ∠BDA (= 90°)
AB = BA (Common hypotenuse)
AC = BD = 2cm
So, ΔACB ≅ ΔBDA
(By RHS congruence rule)

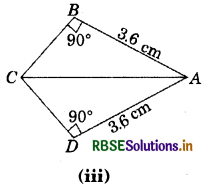
Answer:
Here, ∠ABC = ∠ADC (= 90°)
AB = AD = 3.6cm
AC = AC (Hypotenuse)
ΔABC ≅ ΔADC
By RHS congruence rule) 

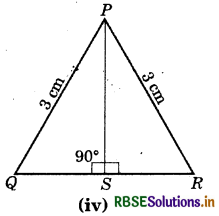
Answer:
Here, ∠PSQ = ∠PSR (= 90°)
PQ = PR = 3 cm (Hypotenuse)
PS = PS (Common in both) 
ΔPSQ ≅ ΔPSR
(By RHS congruence rule)

Question 2.
It is to be established by RHS congruence rule that ΔABC ≅ ΔRPQ. What additional information is needed, if it is given that ∠B = ∠P = 90° and AB = RP?
Answer:
AC = RQ.

Question 3.
In the given figure, BD and CE are altitudes of ΔABC such that BD = CE.

(i) State the three pairs of equal parts in ΔCBD and ΔBCE.
Answer:
Given that BD = CE
Also, ∠BDC = ∠CEB = 90°
BC = CB
(Common in both)

(ii) Is ΔCBD ≅ ΔBCE Why or why not?
Answer:
Yes, by (i), ΔCBD ≅ ΔBCE
(By RHS congruence rule)

(iii) Is ∠DCB = ∠EBC? Why or why not? 
Answer:
Yes, ∠DCB = ∠EBC
Corresponding parts of congruent triangles.

Question 4.
ABC is an isosceles triangle with AB = AC and AD is one of its altitude.

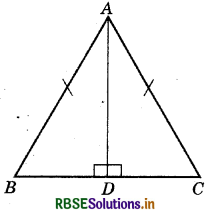
(i) State the three pairs of equal parts in ΔADB and ΔADC.
Answer:
The three equal pairs are AB =AC, ∠ADB = ∠ADC, 
AD = AD (Common side)

(ii) Is ΔADB ≅ ΔADC? Why or why not?
Answer:
Yes ΔADB ≅ ΔADC
∵ ∠ADB = ∠ADC = 90°
AD = AD (Common sides)
BD = DC
Therefore, ΔADB ≅ ΔADC
(By the property of RHS)

(iii) Is ∠B = ∠C? Why or why not?
Answer:
Yes, ∠B = ∠C (By corresponding
parts of congruent triangles)

(iv) Is BD = CD? Why or why not?
Answer:
Yes, BD = CD (By corresponding parts of congruent triangles)