RBSE Solutions for Class 7 Maths Chapter 7 त्रिभुजों की सर्वांगसमता Ex 7.2
Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 7 त्रिभुजों की सर्वांगसमता Ex 7.2 Textbook Exercise Questions and Answers.
RBSE Class 7 Maths Solutions Chapter 7 त्रिभुजों की सर्वांगसमता Ex 7.2
प्रश्न 1.
निम्न में आप कौनसे सर्वांगसम प्रतिबन्धों का प्रयोग करेंगे?
(a) दिया है: AC = DE, AB = DE, BC = EF
इसलिए, ΔABC ≅ ΔDEF
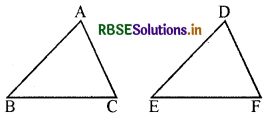
हल:
SSS (भुजा-भुजा-भुजा) सर्वांगसमता प्रतिबन्ध द्वारा,
ΔABC ≅ ΔDEF
(b) दिया है : ZX = RP, RQ = ZY
∠PRQ = ∠XZY
इसलिए, ΔPQR ≅ ΔXYZ
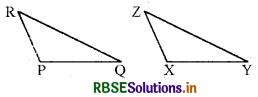
हल:
SAS (भुजा-कोण-भुजा) सर्वांगसमता प्रतिबन्ध द्वारा,
ΔPOR ≅ ΔXYZ
(c) दिया है : ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
इसलिए, ΔLMN ≅ ΔGFH
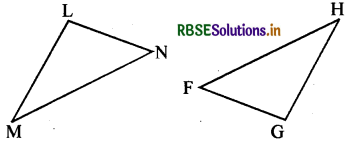
हल:
ASA (कोण-भुजा-कोण) सर्वांगसमता प्रतिबन्ध द्वारा,
ΔLMN ≅ ΔGFH
(d) दिया है : EB = DB,
AE = BC
∠A = ∠C = 90°
इसलिए, ΔABE ≅ ΔCDB
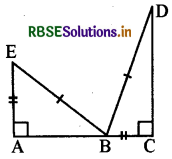
हल:
RHS (समकोण-कर्ण-भुजा) सर्वांगसमता प्रतिबन्ध द्वारा,
ΔABE ≅ ΔCDB

प्रश्न 2.
आप ΔART ≅ ΔPEN दर्शाना चाहते हैं,
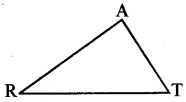
(a) यदि आप SSS सर्वांगसमता प्रतिबन्ध का प्रयोग करें तो आपको दर्शाने की आवश्यकता है :
(i) AR =
(ii) RT =
(iii) AT =
हल:
ΔART ≅ ΔPEN को SSS सर्वांगसमता प्रतिबन्ध द्वारा दर्शाने के लिए दर्शाना होगा :
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b) यदि यह दिया गया है कि ∠T = ∠N और आपको SAS प्रतिबन्ध का प्रयोग करना है, तो आपको आवश्यकता होगी:
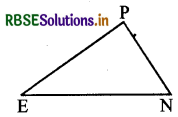
(i) RT =
और (ii) PN =
हल:
यदि m∠T = m∠N और SAS सर्वांगसमता प्रतिबन्ध द्वारा दर्शाने के लिए हमें दर्शाना होगा :
(i) RT = EN
और (ii) PN = AT
(c) यदि यह दिया गया है कि AT = PN और आपको ASA प्रतिबन्ध का प्रयोग करना है तो आपको आवश्यकता होगी।
(i) ? =
(ii) ? =
हल:
यदि AT = PN और ASA सर्वांगसमता के प्रयोग के लिए आवश्यकता होगी :
(i) ∠RAT = ∠EPN
और (ii) ∠ATR = ∠PNE
प्रश्न 3.
आपको ΔAMP ≅ ΔAMQ दर्शाना है। निम्न चरणों में, रिक्त कारणों को भरिए।
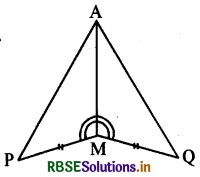
|
क्रम |
कारण |
|
(i) PM = QM |
(i) ...... |
|
(ii) ∠PMA = ∠QMA |
(ii) ........ |
|
(ii) AM = AM |
(iii) …… |
|
(iv) ΔAMP ≅ ΔAMQ |
(iv) ........ |
हल:
कारण क्रमवार नीचे दिये गये हैं :
(i) दिया है
(ii) दिया है
(iii) उभयनिष्ठ
(iv) SAS सर्वांगसमता प्रतिबन्ध ।
प्रश्न 4.
ΔABC में, ∠A = 30°, ∠B = 40° और ∠C = 110°
ΔPQR में, ∠P=30°, ∠Q =40° और ∠R= 110°
एक विद्यार्थी कहता है कि AAA सर्वांगसमता प्रतिबन्ध से ΔABC ≅ ΔPQR है। क्या यह कथन सत्य है? क्यों या क्यों नहीं?
हल:
दो त्रिभुजों में, एक त्रिभुज के तीनों कोण दूसरे त्रिभुज के तीनों कोणों के बराबर हैं तो आवश्यक नहीं त्रिभुज सर्वांगसम हो।
एक ΔABC की रचना कीजिए जिसमें ∠A = 30°, ∠B = 40°, ∠C = 110° और माना BC = 3 cm
दूसरा ΔPQR की रचना करो जिसमें ∠P = 30°, ∠Q = 40°, ∠R = 110° और माना QR = 4 cm
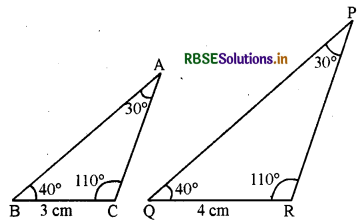
स्पष्टतः त्रिभुजों के संगत कोण बराबर हैं लेकिन यह सर्वांगसम नहीं हैं क्योंकि BC ≠ QR
अतः विद्यार्थी का कथन सत्य नहीं है।

प्रश्न 5.
आकृति में दो त्रिभुज ART तथा OWN सर्वांगसम हैं जिनके संगत भागों को अंकित किया गया है। हम लिख सकते हैं
ΔRAT = ?
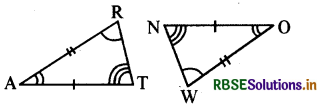
हल:
स्पष्टतः दी गई आकृति ΔRAT ≅ ΔWON
प्रश्न 6.
कथनों को पूरा कीजिए :
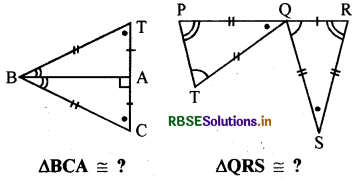
हल:
सर्वांगसम कथन को पूरा करने पर
ΔBCA ≅ ΔBTA
ΔQRS ≅ ΔTPQ
प्रश्न 7.
एक वर्गांकित शीट पर, बराबर क्षेत्रफलों वाले दो त्रिभुजों को इस प्रकार बनाइए कि
(i) त्रिभुज सर्वांगसम हों।
(ii) त्रिभुज सर्वांगसम न हों। आप उनके परिमाप के बारे में क्या कह सकते हैं?
हल:
ΔPQR का क्षेत्रफल
= \(\frac{1}{2}\) × QR × PQ
= \(\frac{1}{2}\) × 4 × 3 वर्ग इकाई
= 6 वर्ग इकाई
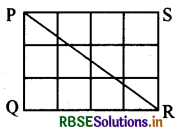
और ΔSRP का क्षेत्रफल
= \(\frac{1}{2}\) × SR × SP
= \(\frac{1}{2}\) × 3 × 4 वर्ग इकाई
= 6 वर्ग इकाई
∴ ΔPQR का क्षेत्रफल = ΔRSP का क्षेत्रफल ΔPQR और ΔRSP में,
· PQ = RS
∠Q = ∠S
और PR = RP
∴ RHS सर्वांगसमता प्रतिबन्ध द्वारा
ΔPOR ≅ ΔRSP
(ii) यहाँ ΔABC का क्षेत्रफल
= \(\frac{1}{2}\) × BC × AB
= \(\frac{1}{2}\) × 5 × 4 वर्ग इकाई
= 10 वर्ग इकाई
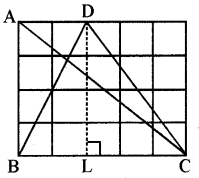
और ΔDBC का क्षेत्रफल
= \(\frac{1}{2}\) × BC × DL
= (\(\frac{1}{2}\) × 5 × 4) वर्ग इकाई
= 10 वर्ग इकाई
∴ ΔABC का क्षेत्रफल = ΔDBC का क्षेत्रफल लेकिन आकृति द्वारा ये त्रिभुज सर्वांगसम नहीं हैं।
लेकिन इस दशा में उनके परिमाप समान नहीं होंगे।

प्रश्न 8.
आकृति में एक सर्वांगसम भागों का एक अतिरिक्त युग्म बताइए जिससे ΔABC और ΔPQR सर्वांगसम हो जाएँ। आपने किस प्रतिबन्ध का प्रयोग किया?
हल:
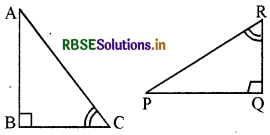
ΔABC ≅ ΔPQR सिद्ध करने के लिए संगत भागों के एक अतिरिक्त युग्म की आवश्यकता होगी वह है BC = QR
इसमें ASA सर्वांगसम प्रतिबन्ध का प्रयोग किया।
प्रश्न 9.
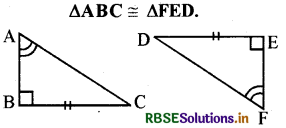
चर्चा कीजिए, क्यों?
हल:
ΔABC ≅ ΔFED क्योंकि,
∠C = ∠D (∠A = ∠F, ∠B = ∠E
∴ तीसरा कोण ∠C = तीसरा कोण ∠D)
BC = DE (दिया है)
और ∠B = ∠E (दिया है)
अतः, ASA सर्वांगसम प्रतिबन्ध से
ΔABC ≅ ΔFED
