RBSE Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.2
Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.2 Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 7. Students can also read RBSE Class 7 Maths Important Questions for exam preparation. Students can also go through RBSE Class 7 Maths Notes to understand and remember the concepts easily. Students can access the data handling class 7 extra questions with answers and get deep explanations provided by our experts.
RBSE Class 7 Maths Solutions Chapter 7 Congruence of Triangles Ex 7.2
Question 1.
Which congruence criterion do you use in the following?
(a) Given : AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
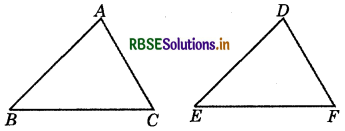
Answer:
SSS congruence criterion
(b) Given : ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
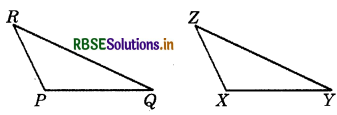
Answer:
SAS congruence criterion
(c) Given : ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
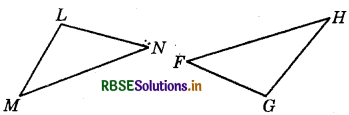
Answer:
ASA congruence criterion
(d) Given : EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB
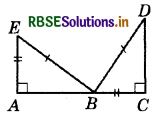
Answer:
RHS Congruence Criterion

Question 2.
You want to show that ΔART ≅ ΔPEN.
(a) If you have to use SSS criterion, then you need to show
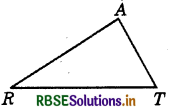
(i) AR =
(ii) RT =
(iii) AT =
Answer:
(i) AR = PE
(ii) RT = EN,
(iii) AT = PN
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and
(ii) PN =
Answer:
(i) RT = EN
(ii) PN = AT
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ?
(ii) ?
Answer:
(i) ∠ATR = ∠PNE
(ii) ∠TAR = ∠NPE
Question 3.
You have to show that ΔAMP ≅ ΔAMQ.
In the following proof, supply the missing reasons:
|
Steps |
Reasons |
|
(i) PM = QM |
(i) …………………. |
|
(ii) ∠PMA = ∠QMA |
(ii) …………………. |
|
(iii) AM = AM |
(iii) …………………. |
|
(iv) ΔAMP ≅ ΔAMQ |
(iv) …………………. |
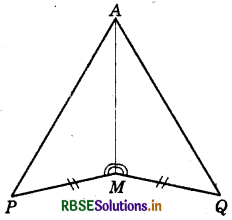
Answer:
|
Steps |
Reasons |
|
(i) PM = QM |
(i) Given |
|
(ii) ∠PMA = ∠QMA |
(ii) Given |
|
(iii) AM = AM |
(iii) Common |
|
(iv) ΔAMP ≅ ΔAMQ |
(iv) SAS ongruence criterion |

Question 4.
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C= 110°.
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
Answer:
No, student is not justified because AAA is not a criterion for congruence of triangles.
Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ΔRAT ≅ ?
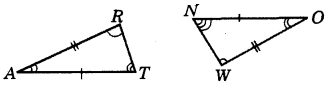
Answer:
ΔRAT ≅ ΔWON
(By SAS congruence rule)
Question 6.
Complete the congruence state¬ment :
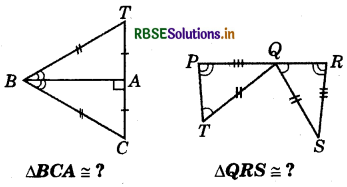
Answer:
ΔBCA ≅ ΔBTA (By SSS rule)
ΔQRS ≅ ΔTPQ (By SSS rule)
Question 7.
In a squared sheet, draw two triangles of equal areas such that:
(i) the triangles are congruent.
(ii) the triangles are not congruent. What can you say about their peri¬meters?
Answer:
In a squared sheet, draw ΔABC and ΔPQR.
When two triangles have equal areas and
(i) these triangles are congruent, i.e.
ΔABC ≅ ΔPQR.
(By SSS congruence rule)
Then, their perimeters are same because length of sides of first triangle are equal to the. length of sides of another triangle by SSS congruence rule.
(ii) But, if the triangles are not congruent, then their perimeters are not same because lengths of sides of first triangle are not equal to the length of corresponding sides of another triangle.
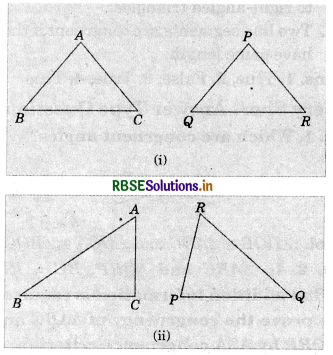

Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Answer:
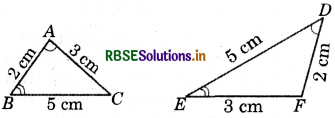
In ΔABC and ΔDEF
AB = DF = 2 cm
BC = ED = 5 cm
AC = EF = 3 cm
∠BAC = ∠EDF
∠ABC = ∠DEF
But ΔABC is not congruent to ΔDEF.
Question 9.
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
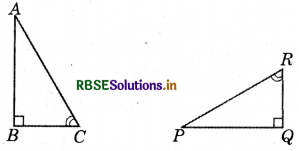
Answer:
BC = QR by ASA congruence rule.

Question 10.
Explain, why ΔABC = ΔFED
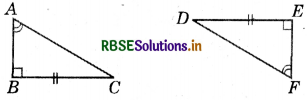
Answer:
In ΔABC and ΔFED,
∠ABC = ∠FED = 90°
BC = ED
∠ACB = ∠FDE
(Using angle sum property of a triangle)
∴ ΔABC ≅ ΔFED
(SAS congruence criterion.)

- RBSE Solutions for Class 7 Maths Chapter 8 Comparing Quantities Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Intext Questions
- RBSE Class 7 Maths Notes in Hindi & English Medium Pdf Download
- RBSE Class 7 Maths Important Questions in Hindi & English Medium
- RBSE Solutions for Class 7 Maths in Hindi Medium & English Medium
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Ex 12.2
- RBSE Solutions for Class 6 Maths Chapter 12 अनुपात और समानुपात Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 5 रेखा एवं कोण Intext Questions
- RBSE Solutions for Class 7 Maths Chapter 9 परिमेय संख्याएँ Ex 9.1
- RBSE Solutions for Class 7 Maths Chapter 4 सरल समीकरण Ex 4.3
- RBSE Class 7 Maths Important Questions Chapter 13 घातांक और घात