RBSE Solutions for Class 7 Maths Chapter 6 त्रिभुज और उसके गुण Intext Questions

Rajasthan Board RBSE Solutions for Class 7 Maths Chapter 6 त्रिभुज और उसके गुण Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 7 Maths Solutions Chapter 6 त्रिभुज और उसके गुण Intext Questions

(प्रयास कीजिए - पृष्ठ 125-126)

प्रश्न 1.
ΔABC के छः अवयवों (तीन भुजाओं तथा तीन कोणों) के नाम लिखिए।
हल:
ΔABC की तीन भुजाएँ AB, BC तथा CA और तीन कोण A, B तथा C हैं।

प्रश्न 2.
लिखिए: (i) ΔPQR के शीर्ष की सम्मुख भुजा
(ii) ΔLMN की भुजा LM का सम्मुख कोण
(iii) ΔRST की भुजा RT का सम्मुख शीर्ष।
हल:
(i) ΔPQR में शीर्ष Q की सम्मुख भुजा RP है।
(ii) ΔLMN भुजा की LM का सम्मुख कोण ZN है ।
(iii) ΔRST की भुजा RT का सम्मुख शीर्ष S है।

 

प्रश्न 3.
आकृतियाँ देखिए तथा त्रिभुजों में प्रत्येक का वर्गीकरण कीजिए :
(a) भुजाओं के आधार पर
(b) कोणों के आधार पर

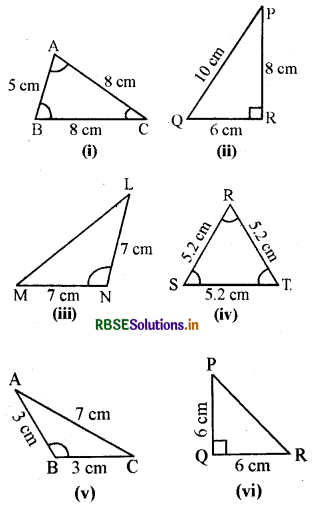
हल:
(a) भुजाओं के आधार पर वर्गीकरण :
समद्विबाहु त्रिभुज : (i), (iii), (v) और (vi)
विषमबाहु त्रिभुज : (ii)
समबाहु त्रिभुज : (iv)

(b) कोणों के आधार पर वर्गीकरण :
न्यूनकोण त्रिभुज : (i) और (iv)
समकोण त्रिभुज : (ii) और (vi)
अधिक कोण त्रिभुज : (iii) और (v)

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 127-I)

प्रश्न 1.
एक त्रिभुज में कितनी माध्यिकाएँ हो सकती
हल:
एक त्रिभुज में तीन शीर्ष तथा उनके सम्मुख तीन भुजाएँ होती हैं, इसलिए प्रत्येक शीर्ष से एक माध्यिका होती है। अतः त्रिभुज की तीन माध्यिकाएँ होती हैं।

प्रश्न 2.
क्या एक माध्यिका पूर्णतया त्रिभुज के अन्दर में स्थित होती है? (यदि आप समझते हैं कि यह सत्य नहीं है तो उस स्थिति के लिए एक आकृति खींचिए।)
हल:
हाँ, एक माध्यिका पूर्णतया त्रिभुज के अन्दर स्थित होती है।

(सोचिए, चर्चा कीजिए और लिखिए। - पृष्ठ 127-II)

प्रश्न 1.
एक त्रिभुज में कितने शीर्ष हो सकते हैं?
हल:
एक त्रिभुज में तीन शीर्ष होते हैं।

प्रश्न 2.
निम्न त्रिभुजों में A से \(\overline{\mathrm{BC}}\) तक अनुमान से शीर्षलम्ब खींचिए :

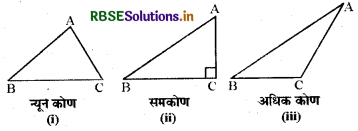
हल:
अनुमान से त्रिभुजों में A से \(\overline{\mathrm{BC}}\) पर शीर्ष लम्ब निम्न प्रकार है :

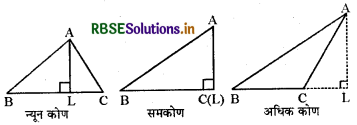
प्रत्येक स्थिति में AL शीर्षलम्ब है।

प्रश्न 3.
क्या एक शीर्षलम्ब पूर्णतया त्रिभज के अभ्यन्तर में सदैव स्थित होगा? (यदि आप समझते हैं कि यह सत्य होना आवश्यक नहीं है तो उस स्थिति के लिए एक आकृति खींचिए।)
हल:
शीर्षलम्ब सदैव त्रिभुज के अभ्यन्तर में स्थित नहीं होगा।

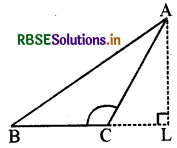
ΔABC अधिक कोण त्रिभुज इस प्रकार है कि ∠C अधिक कोण है तथा AL शीर्ष A से शीर्षलम्ब है। स्पष्टतः । भुजा BC पर स्थित नहीं है। यह BC की बढ़ी हुई भुजा पर स्थित है। इस स्थिति में शीर्षलम्ब AL त्रिभुज के बाहर स्थित होगा (बिन्दु A को छोड़कर)।

प्रश्न 4.
क्या आप कोई ऐसा त्रिभुज सोच सकते हैं; जिसके दो शीर्षलम्ब उसकी दो भुजाएँ ही हों?
हल:
हाँ, यदि त्रिभुज ABC, ∠C पर समकोण हो तो चित्र में दर्शाए अनुसार शीर्ष A और B से शीर्षलम्ब AC और BC क्रमशः ΔABC की दो भुजाएँ हैं। B

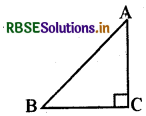
प्रश्न 5.
क्या किसी त्रिभुज की माध्यिका व शीर्षलम्ब एक ही रेखाखण्ड हो सकता है?
हल:
हाँ, हो सकता है। समबाहु की स्थिति में माध्यिका और शीर्षलम्ब एक ही रेखाखण्ड पर होते हैं जैसा कि आकृति में दर्शाया गया है। यह समद्विबाहु त्रिभुज के सन्दर्भ में भी सत्य है।

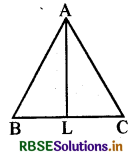
(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 130-I)

प्रश्न 1.
एक त्रिभुज के लिए बाह्य कोण भिन्नभिन्न प्रकार से बनाए जा सकते हैं। इनमें से तीन, निम्न प्रकार से दिखाए गए हैं :

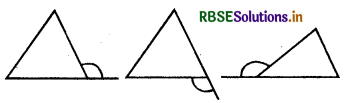
इनके अतिरिक्त तीन और प्रकार से भी बाह्य कोण बनाए जा सकते हैं। उन्हें भी अनुमान से बनाइए।
हल:
तीन और प्रकार निम्न विधि से बाह्य कोण बनाए जा सकते हैं :

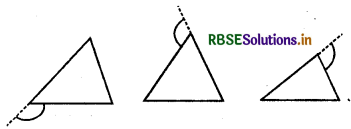
प्रश्न 2.
किसी त्रिभुज के एक शीर्ष पर बने दोनों बाह्य कोण क्या परस्पर समान होते हैं?
हल:
ΔABC की भुजा AC को आगे बढ़ाओ और किरण AY बनाओ तो C पर ∠BCY भी एक बाह्य कोण होगा।

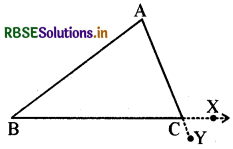
स्पष्ट है ∠ACX और ∠BCY ऊर्ध्वाधर सम्मुख कोण हैं।
∴ ∠ACX = ∠BCY
∴ त्रिभुज के प्रत्येक शीर्ष पर बाह्य कोणों का एक युग्म होगा जो आपस में समान होंगे।

प्रश्न 3.
किसी त्रिभुज के एक बाह्य कोण और उसके संलग्न अन्तःकोण के योग के बारे में आप क्या कह सकते हैं?
हल:
ΔABC के शीर्ष C पर बाह्य कोण ∠ACX है तथा ∠ACB संलग्न अन्त:कोण है।..

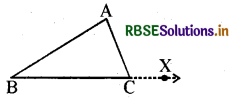
स्पष्टतः ∠ACX + ∠ACB = 180°
अन्तः बाह्य कोण और संलग्न अन्तःकोण रैखिक युग्म बनाते हैं।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 130-II)

प्रश्न 1.
प्रत्येक दशा में अन्तःसम्मुख कोणों के बारे में आप क्या कह सकते हैं जबकि बाह्य कोण है :
(i) एक समकोण
(ii) एक अधिक कोण
(iii) एक न्यून कोण।
हल:
(i) यदि बाह्य कोण समकोण होगा तो अन्तःसम्मुख कोणों का योग भी 90° का होगा यानी इनमें से प्रत्येक कोण न्यून कोण होगा।
(ii) यदि बाह्य कोण अधिक कोण हो तो दोनों अन्तःसम्मुख कोणों में से या तो दोनों न्यून कोण होंगे अथवा एक अधिक कोण और एक न्यून कोण होगा।
(iii) यदि बाह्य कोण एक न्यून कोण हो तो प्रत्येक | अन्तःसम्मुख कोण न्यून कोण होगा।

प्रश्न 2.
क्या किसी त्रिभुज का कोई बाह्य कोण एक सरल कोण भी हो सकता है?
हल:
त्रिभुज का कोई भी बाह्य कोण सरल कोण नहीं हो सकता क्योंकि संलग्न अन्तःकोण शून्य नहीं हो सकता है।

(प्रयास कीजिए - पृष्ठ 130)

प्रश्न 1.
किसी त्रिभुज में एक बाह्य कोण की माप 170° है और उसके अन्तःसम्मुख कोणों में से एक की माप 25° है। दूसरे अन्तःसम्मुख कोण की माप ज्ञात कीजिए।
हल:
माना APQR की भुजा QR को आगे बढ़ाया तो बाह्य कोण ∠PRS इस प्रकार बना कि ∠PRS = 70°

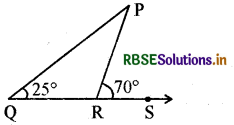
माना ∠Q = 25° बाह्य कोण प्रमेय द्वारा
या ∠PRS = ∠Q + AP
या 70° = 25° + ∠P
∠P = 70° - 25° = 45°
अतः दूसरा अन्तःसम्मुख कोण 45° का है।

प्रश्न 2.
किसी त्रिभुज के दो अन्तःसम्मुख कोणों की माप 60° और 80° है। उसके बाह्य कोण की माप ज्ञात कीजिए।
हल:
माना त्रिभुज ABC की भुजा BC को आगे बढ़ाते हैं तो एक बाह्य कोण ACD बना। माना ∠A = 80° और ∠B = 60°

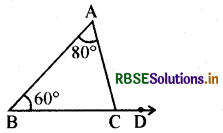
बाह्य कोण प्रमेय द्वारा
∠ACD = ∠A + ∠B
या ∠ACD = 80° + 60° = 140°
अतः, बाह्य कोण की माप 140° होगी।

प्रश्न 3.
क्या इस आकृति में कोई त्रुटि है? टिप्पणी करें।

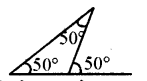
हल:
आकृति में बाह्य कोण अन्तःसम्मुख कोणों के योग के बराबर नहीं है क्योंकि 50° 450° + 50° ।
अतः दिए गए आँकड़े गलत हैं।

(प्रयास कीजिए - पृष्ठ 134)

प्रश्न 1.
एक त्रिभुज के दो कोण 30° तथा 80° हैं। इस त्रिभुज का तीसरा कोण ज्ञात कीजिए।
हल:
माना ABC त्रिभुज है जिसमें ∠B = 30° और ∠C = 80° तो, हमें तीसरा कोण A ज्ञात करना है।
अब, ∠B + ∠C = 30° + 80° = 110°
त्रिभुज कोण के गुण द्वारा
∠A + ∠B + ∠C = 180°
या ∠A + 110° = 180° [∵ ∠B + ∠C = 110°|
या ∠A = 180° - 110°
या ∠A = 70°

प्रश्न 2.
किसी त्रिभुज का एक कोण 80° है तथा शेष दोनों कोण बराबर हैं। बराबर कोणों में प्रत्येक की माप ज्ञात कीजिए।
हल:
माना त्रिभुज ABC में ∠A = 80° और ∠B = ∠C
त्रिभुज कोण के गुण द्वारा
या ∠A + ∠B + ∠C = 180°
या 80° + ∠B + ∠B = 180° [∵∠A = 80° और ∠C = ∠B]
या 80° + 2∠B = 180°
या 2∠B = 180° - 80°
या 2∠B = 100°
या ∠B = \(\left(\frac{100}{2}\right)^{\circ}\) = 50°
अतः, शेष दो कोणों की माप 50° है।

प्रश्न 3.
किसी त्रिभुज के तीनों कोणों में 1: 2:1 का अनुपात है।त्रिभुज के तीनों कोण ज्ञात कीजिए।त्रिभुज का दोनों प्रकार से वर्गीकरण भी कीजिए।
हल:
माना त्रिभुज के कोण x, 2x और x हैं तो
x + 2x + x = 180°
या 4x = 180°
या x = \(\frac{180}{4}\) = 45°
अतः, त्रिभुज के कोण 45°, 90° और 45° होंगे।
अतः, त्रिभुज समकोण त्रिभुज है और यह एक समद्विबाहु त्रिभुज है।

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 134)

प्रश्न 1.
क्या कोई ऐसा त्रिभुज सम्भव है जिसके दो कोण समकोण हों?
हल:
नहीं, ऐसा कोई त्रिभुज नहीं हो सकता जिसमें दो समकोण हों। क्योंकि त्रिभुज के तीनों कोणों का योग दो समकोण होता है।

प्रश्न 2.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें दो कोण अधिक कोण हों?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है जिसमें दो कोण अधिक कोण हों। क्योंकि इस स्थिति में तीन कोणों का योग दो समकोण से अधिक हो जाएगा।

प्रश्न 3.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें दो कोण न्यून कोण हों?
हल:
हाँ, ऐसा त्रिभुज सम्भव है जिसमें दो न्यून कोण हों।

प्रश्न 4.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° से अधिक हों?
हल:
नहीं, ऐसा कोई त्रिभुज सम्भव नहीं है जिसमें सभी तीनों कोण 60° से अधिक हों। इस स्थिति में तीनों कोणों का योग 180° से अधिक हो जाएगा। लेकिन यह 180° के बराबर होना चाहिए।

प्रश्न 5.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° के हों?
हल:
हाँ, ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° के हों।

प्रश्न 6.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° से कम के हो?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है जिसमें तीनों कोण 60° से कम हों। इस स्थिति में त्रिभुज के तीनों कोणों का योग 180° से कम होगा; जबकि यह 180° के बराबर होना चाहिए।

(प्रयास कीजिए - पृष्ठ 135)

प्रश्न 1.
प्रत्येक आकृति में कोण x का मान ज्ञात कीजिए।

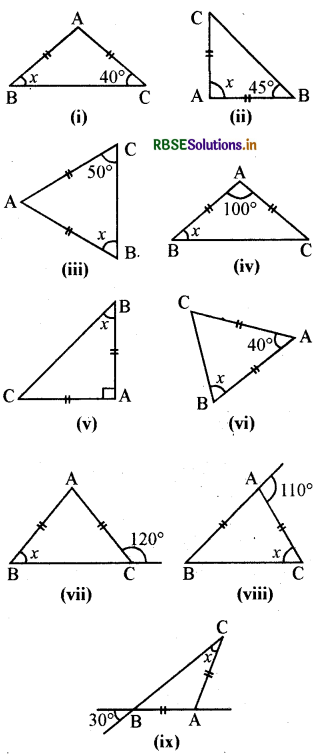
हल:
सबसे पहले हम सभी त्रिभुजों के शीर्षों को नामांकित करेंगे।
आकृति (i) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∠B = ∠C
या x = 40°

आकृति (ii) में ΔABC एक समद्विबाहु त्रिभुज है । जिसमें
AB = AC
∠B = ∠C
45° = ∠C

कोण योग गुण द्वारा
∠A + ∠B + ∠C = 180°
या x + 45° + 45° = 180°
या x + 90° = 180°
x = 180° - 90°
x = 90°

आकृति (iii) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
LB = LC
x = 50°

आकृति (iv) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∠B = ∠C
x = ∠C
कोण योग गुण द्वारा .
∠A + ∠B + ∠C = 180°
या 100° + x + x = 180°
या 2x = 180° - 100°
या 2x = 80°
या x = \(\left(\frac{80}{2}\right)^{\circ}\) = 40°

आकृति (v) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∴ ∠B = ∠C
या x = ∠C
कोण योग गुण द्वारा
∠A + ∠B + ∠C = 180°
या 90° + x + x = 180°
या 2x = 180° - 90°
या 2x = 90°
या x = \(\left(\frac{90}{2}\right)^{\circ}\) = 45°

आकृति (vi) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∴ ∠B = ∠C
या x = ∠C कोण योग गुण द्वारा
या ∠A + ∠B∠C = 180°
या 40° + x + x = 180°
या 2x = 180° - 40°
या 2x = 140°
या x = \(\left(\frac{140}{2}\right)^{\circ}\) = 70°

आकृति (vii) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∠B = ∠C
x = ∠C
क्योंकि बाह्य कोण और संलग्न अन्त:कोण रैखिक युग्म बनाते हैं
∠C + 120° = 180°
या x = 180 - 120°
= 60°

आकृति (viii) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∠B = ∠C
∠B = x
क्योंकि बाह्य कोण और संलग्न अन्त:कोण रैखिक युग्म बनाते हैं
110° + ∠A = 180°
∠A = 180° - 110° = 70°

कोण योग गुण द्वारा
∠A + ∠B + ∠C = 180°
70° + x + x = 180°
2x = 180° - 70°
2x = 110°
x = \(\left(\frac{110}{2}\right)^{\circ}\) = 55°

आकृति (ix) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC
∠B = ∠C
∠B = x साथ ही,
∠B = 30° [ऊर्ध्वाधर सम्मुख कोण]
x = 30° [∠B = x]

प्रश्न 2.
प्रत्येक आकृति में कोण x तथा y का मान ज्ञात कीजिए।

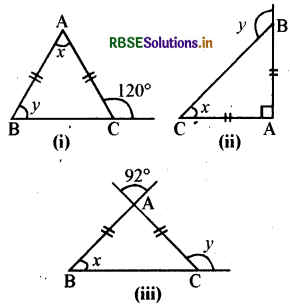
हल:
सर्वप्रथम सभी त्रिभुजों को चित्रानुसार नामांकित करेंगे।
आकृति (i) में बाह्य कोण और अन्तः संलग्न कोण रैखिक युग्म बनाते हैं।
∠C + 120° = 180°
या ∠C = 180° - 120° = 60°
क्योंकि ΔABC समद्विबाहु त्रिभुज है जिसमें AB = AC, इसलिए
∠B = ∠C
या ∠B = 60°
अर्थात् y = 60°

कोण योग गुण द्वारा
∠A + ∠B + ∠C = 180°
या x + y + 60° = 180°
या x + 60° + 60° = 180°
या x + 120° = 180°
x = 180° - 120° = 60°
अतः, x = 60° और y = 60°

आकृति (ii) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC, इसलिए ∠B = ∠C
∠B = x
या ∠B + ∠C = 90°
या x + x = 90° [∵ ∠ = x]
या 2x = 90°
या x = 45°
लेकिन ∠B + y = 180°
x + y = 180° [∵ ∠B = x]
y = 180° - 45° [∵ x = 45°]
y = 135°
अतः, x = 45° और y = 135°

आकृति (iii) में ΔABC समद्विबाहु त्रिभुज है जिसमें
AB = AC, इसलिए ∠B = ∠C
∠B = ∠C = x और
∠A = 92°
[ऊर्ध्वाधर सम्मुख कोण]

कोण योग गुण द्वारा
∠A + ∠B + ∠C = 180°
या 92° + x + x = 180°
2x = 180° - 92° = 88°
x = \(\left(\frac{88}{2}\right)^{\circ}\) = 44°
∠C + y = 180° [रैखिक युग्म]
y = 180° - 44° = 136° [∵ ∠C = x = 44°]
अतः, x = 44° और y = 136°

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 139)

प्रश्न 1.
किसी त्रिभुज में क्या उसके कोई दो कोणों का योग तीसरे कोण से सदैव अधिक होता है?
हल:
नहीं, त्रिभुज में किन्हीं दो कोणों का योग तीसरे कोण से सदैव बड़ा नहीं होता है।

(प्रयास कीजिए - पृष्ठ 141)

प्रश्न 1.
निम्न आकृतियों में अज्ञात लम्बाई x ज्ञात कीजिए:

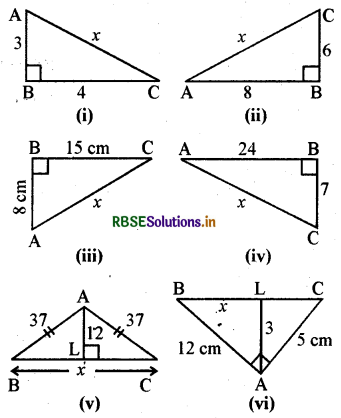
हल:
सर्वप्रथम दिये गये चित्रों में सभी त्रिभुजों को नामांकित करेंगे।
आकृति (i) में ΔABC में कोण ∠B समकोण है।
∴ पाइथागोरस प्रमेय द्वारा
AC² = AB² + BC²
इसलिए, x² = 3² + 4²
x² = 9 + 16
x² = 25 = 5²
x = 5

आकृति (ii) में ΔABC में ∠B समकोण है।
पाइथागोरस प्रमेय द्वारा
AC² = AB² + BC²
इसलिए, x² = 8² + 6²
या x² = 64 + 36
x² = 100 = 10²
x = 10

आकृति (iii) में ΔABC में ∠B समकोण है।
पाइथागोरस प्रमेय द्वारा
AC² = AB² + BC²
इसलिए, x² = 8² + 15²
x² = 64 + 225
x² = 289 = 172
या x = 17

आकृति (iv) मैं ΔABC में ∠B समकोण है।
∴ पाइथागोरस प्रमेय द्वारा
AC² = AB² + BC²
इसलिए, x² = 24² + 7²
x² = 576 + 49
या x² = 625 = 25²
या x = 25

आकृति (v) में समकोण ΔALB और ΔALC में पाइथागोरस प्रमेय का प्रयोग करके
BL² = AB² - AL²
इसलिए, BL² = 37² - 12²
या BL² = (37 + 12) (37 - 12)
या BL² = 49 × 25 = (7 × 5)²
BL = 7 x 5 = 35
इसी प्रकार, CL = 35
BC = BL + LC = 35 + 35 = 70
या x = 70

आकृति (vi) में ΔALB में पाइथागोरस प्रमेय का प्रयोग करके
BL² = AB² - AL²
इसलिए, x² = 12² - 3²
या x² = 144 - 9
या x² = 135
या x = \(\sqrt{135}\)

(सोचिए, चर्चा कीजिए और लिखिए - पृष्ठ 143)

प्रश्न 1.
त्रिभुज PQR का कोण P एक समकोण है। इसकी सबसे लम्बी भुजा कौनसी है?
हल:

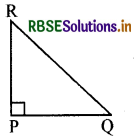
सबसे लम्बी भुजा सबसे R बड़े कोण के सामने होती है। ΔPQR में सबसे बड़ा कोण 90°, जो कोण P दिया है। अतः सबसे लम्बी भुजा कोण P के सामने होगी। अतः यह QR होगी।

प्रश्न 2.
त्रिभुज ABC का कोण B एक समकोण है। इसकी सबसे लम्बी भुजा कौनसी है?
हल:

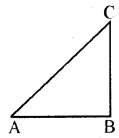
क्योंकि सबसे लम्बी भुजा सबसे बड़े कोण के सामने होती है। ΔABC में ∠B सबसे बड़ा कोण है अर्थात् ∠B = 90°। अतः सबसे लम्बी भुजा ∠B के सामने की भुजा AC होगी।

प्रश्न 3.
किसी समकोण त्रिभुज में सबसे लम्बी भुजा कौनसी होती है?
हल:
किसी समकोण त्रिभुज में सबसे लम्बी भुजा कर्ण होती है।

प्रश्न 4.
किसी आयत में विकर्ण पर बने वर्ग का क्षेत्रफल उसकी लम्बाई तथा चौड़ाई पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है। यह बौधायन का प्रमेय है। इसकी पाइथागोरस गुण से तुलना कीजिए।
हल:
पाइथागोरस गुण के अनुसार, किसी समकोण त्रिभुज में कर्ण पर बने वर्ग का क्षेत्रफल दोनों पादों पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है। बौधायन प्रमेय के अनुसार, किसी आयत में विकर्ण पर बने वर्ग का क्षेत्रफल उसकी लम्बाई तथा चौड़ाई पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है।

माना कि आयत की लम्बाई और चौड़ाई क्रमशः a और b है तथा इसका विकर्ण c है। इसलिए, विकर्ण पर बने वर्ग का क्षेत्रफल = cx² = c², आगे इनकी भुजाओं पर बने वर्गों के क्षेत्रफल a² और b² हैं।
इसलिए, c² = a² + b² (बौधायन प्रमेय द्वारा) स्पष्ट है कि यही वह प्रथम कथन था जिसे आजकल पाइथागोरस प्रमेय के नाम से जानते हैं।